LoginSignup
18
11

More than 3 years have passed since last update.

@as_kuyain株式会社ディー・エヌ・エー

行列による画像の自由変形をWebGLで実装する

Last updated at Posted at 2020-02-03

始めに

free-deformation.gif
画像編集ソフトでよく実装されている、いわゆる自由変形をWebGL上でVertex Bufferに入力された座標を編集することなく 行列のみを使用し矩形の4頂点の座標を任意で指定し変形 でするものを作ってみました。

Vertex Bufferの変更による変形と行列による変形は何が違うのか

3D用のレンダリングAPIを使用して矩形の自由変形を実装しようとする時、まず思いつくのはVertex Bufferの座標を編集して実装する方法が最も簡単な実装と思われます。

しかし、そこであえて行列の変換により矩形の自由変形で実装するとVertex Bufferの座標の編集の実装と比べどのような違いが表れるのでしょうか？
no_deformation.png
行列による矩形の自由変形の実装はVertex Bufferの座標の修正による自由変形と比べ明確な利点があります。

それはWebGL等の3DレンダリングAPIを使用して画像を描画しようとする場合は3角形のポリゴンを組み合わせてレンダリングを行うことになります。つまり矩形を描画する際には3角形のポリゴンを2枚用いることになります。
deformation_vertex_buffer.png
矩形を2枚のポリゴンに分割して、ただ単純にVertex Bufferの座標を編集するとポリゴンとポリゴンのつなぎ目で変形が非連続的になり、そのつなぎ目の部分が歪んで不自然になります。

Vertex Bufferの座標を編集するやり方でこのつなぎ目の歪みを抑制するには矩形をより多くのポリゴンに分割して変形を行えば良いのですが、厳密にするため細かくポリゴンを分割してしまうとVertex Bufferの編集の手間や処理速度が犠牲となります。
deformation_matrix.png
そこで行列を使用し線形空間を保ちつつ且つ矩形の4頂点を任意の座標に配置することの出来る実装ができれば破断なく、高速で単純な実装が実現できるわけです。

実装

定義

まずは矩形の定義と、その矩形をどのように処理するかを定義します。
definition.png
矩形の左上、始点をの座標を(0, 0)、右上の座標を(1, 0)、左下の座標を(0, 1)、右下、終点の座標を(1, 1)と定義し、これらの点を順番に点S、点X、点Y、点Eと命名します。

そして、これらの各4頂点の座標を行列により任意で配置出来る行列を作成出来る処理を考えます。

JavaScriptの関数の定義

/**
 * (0, 0)を始点、(1, 1)を終点とする正方形に対し4頂点を任意座標に配置できる行列を設定する。
 * @param mat 計算結果の出力先の行列
 * @param sx 始点のX座標
 * @param sy 始点のY座標
 * @param xx X点のX座標
 * @param xy X点のY座標
 * @param yx Y点のX座標
 * @param yy Y点のY座標
 * @param ex 終点のX座標
 * @param ey 終点のY座標
 */
function setDeformation(mat, sx, sy, xx, xy, yx, yy, ex, ey) {
    // 行列生成の実装
}

始点の座標を任意の座標に配置出来る行列を定義する

まず最初に始点の座標を任意の座標に配置出来る行列を考えます。

これは単に平行移動行列をそのまま用いれば始点の座標を任意の座標に配置することの出来る行列を定義することが出来ます。
move_point_s.png

\begin{bmatrix}
1 & 0 & 0 & S_x \\
0 & 1 & 0 & S_y \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
\end{bmatrix}

setMatrix(
    mat,
    1, 0, 0, sx,
    0, 1, 0, sy,
    0, 0, 0, 0,
    0, 0, 0, 1);

右上と左下の点の座標を任意の座標に配置出来る行列を定義する

次に右上と左下の点の座標を任意の座標に配置出来る行列を考えます。

これは始点から左上の点へのベクトルと始点から左下の点へのベクトルを計算し、その値を行列の要素に設定すれば右上と左下の点の座標を任意の座標に配置することの出来る行列を作成することが出来ます。
move_point_x_and_y.png

\vec{SX}=
\begin{bmatrix}
\vec{SX}_x \\
\vec{SX}_y
\end{bmatrix}
,
\vec{SY}=
\begin{bmatrix}
\vec{SY}_x \\
\vec{SY}_y
\end{bmatrix}

\begin{bmatrix}
\vec{SX}_x & \vec{SY}_x & 0 & 0 \\
\vec{SX}_y & \vec{SY}_y & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}

setMatrix(
    mat,
    xx - sx, yx - sx, 0, 0, 0,
    xy - sy, yy - sy, 0, 0, 0,
    0, 0, 0, 0,
    0, 0, 0, 1);

終点の座標を任意の座標に配置することの出来る行列を定義する

最後に終点の座標を任意の座標に配置出来る行列を考えます。

これは終点以外の始点、右上の点、左下の点に影響を与えないように変形を行う必要があります。これにはベクトルの重みの要素を利用して少々難易度の高い変換を行わなければなりません。

終点以外の頂点の座標に影響を与えないように変形を行う行列を定義する

まずは、どのような形であれ始点、右上の点、左上の点を動かさないように終点のみを動かすことの出来る変換を行う行列を考えます。

基本的にはベクトルの重みに作用し、その結果終点が動くような行列を作り、終点以外に動いた点があればベクトルの重みの作用を打ち消すように行列の各要素を定義していきます。

これを考えると下記のような、重みの要素により終点の座標を変換し終点以外の座標の変化をスケール値で打ち消す行列が出来ます。

\begin{bmatrix}
\frac{1}{y} & 0 & 0 & 0 \\
0 & \frac{1}{x} & 0 & 0 \\
0 & 0 & 0 & 0 \\
\frac{1}{y} - 1 & \frac{1}{x} - 1 & 0 & 1 \\
\end{bmatrix}

move_e_x.png move_e_y.png
しかし、この定義した行列ではまだ不十分であり終点の座標をそのままこの行列に適用しても上手く座標変換を行うことが出来ないので更に考えを深堀りしていく必要があります。
move_with_weight.png
試しに単純に終点の指定の座標をこの行列に適用すると指定した終点の座標と実際に変換された終点の座標でズレが生じてしまいます。

指定の座標に変換後の終点の座標を配置出来るようにする

前項で始点、右上の点、左下の点に影響を与えることなく矩形の変形が出来たわけですが、任意の座標に終点を配置することは叶いませんでした。しかし、前項で作成した行列には下記のような特性があります。
move_with_weight_2.png
指定の数値を座標として置き、指定の座標からY軸と平行な線を引き、その線がY軸と平行な Y = 1 の線と交差する点をAとします。次に指定の数値を座標として置き、指定の座標からX軸と平行な線を引き、その線がX軸と並行な X = 1 交差する点を点Bとします。そして点Xと点Aの線と点Yと点Bの線の交点が変換後の終点となる特性があります。

つまり、この特性を利用して終点の指定から逆算を行いその値を前項の行列に代入することにより任意の座標に終点を配置することの出来る行列を定義することが出来ます。細かい計算過程は省きますが上記の特性を踏まえ計算式を組むと以下のような行列が得られます。

\begin{bmatrix}
\frac{\vec{es}×\vec{ey}}{\vec{ex}×\vec{ey}} & 0 & 0 & 0 \\
0 & \frac{\vec{ex}×\vec{es}}{\vec{ex}×\vec{ey}} & 0 & 0 \\
0 & 0 & 0 & 0 \\
\frac{\vec{es}×\vec{ey}}{\vec{ex}×\vec{ey}} - 1 & \frac{\vec{ex}×\vec{es}}{\vec{ex}×\vec{ey}} - 1 & 0 & 1 
\end{bmatrix}

let exx = xx - ex; // x - e
let exy = xy - ey;
let eyx = yx - ex; // y - e
let eyy = yy - ey;
let esx = sx - ex; // s - e
let esy = sy - ey;

// (x - e) × (y - e) 終点、点X、点Yの三角形の面積
let det = exx * eyy - exy * eyx; 
// (x - e) × (s - e) / ((x - e) × (y - e)) 始点、終点、点Xの三角形と終点、点X、点Yの面積比
let dx = (exx * esy - exy * esx) / det; 
// (s - e) × (y - e) / ((x - e) × (y - e)) 始点、終点、点Yの三角形と終点、点X、点Yの面積比
let dy = (esx * eyy - esy * eyx) / det;

mulMatrix(
    dst,
    dy, 0, 0, 0,
    0, dx, 0, 0,
    0, 0, 0, 0,
    dy - 1, dx - 1, 0, 1);

外積等を使うことはこの数式を作るときには意図はしてはいなかったのですが交点と求める計算を重ね、計算式をまとめていった結果、終点から右上の点のベクトルと終点から左下の点のベクトルとの外積、終点から始点からのベクトルと始点から右上のベクトルの外積、終点から始点へのベクトルと終点から左下のベクトルの外積、これらの各外積の比率がベクトルの重みを操作する行列の要素の式の比率となっているようです。

各4頂点の座標を任意で定義する

最後にこれらの始点移動、右上の点、左下の点の移動、終点移動の各行列を掛け合わせることにより最終的に矩形の各4頂点の座標を任意の座標に配置で設定出来る行列にまとめることが出来ました。
free_deformation.png

\begin{bmatrix}
1 & 0 & 0 & S_x \\
0 & 1 & 0 & S_y \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1 \\
\end{bmatrix}
\begin{bmatrix}
\vec{SX}_x & \vec{SY}_x & 0 & 0 \\
\vec{SX}_y & \vec{SY}_y & 0 & 0 \\
0 & 0 & 0 & 0 \\
0 & 0 & 0 & 1
\end{bmatrix}
\begin{bmatrix}
\frac{\vec{es}×\vec{ey}}{\vec{ex}×\vec{ey}} & 0 & 0 & 0 \\
0 & \frac{\vec{ex}×\vec{es}}{\vec{ex}×\vec{ey}} & 0 & 0 \\
0 & 0 & 0 & 0 \\
\frac{\vec{es}×\vec{ey}}{\vec{ex}×\vec{ey}} - 1 & \frac{\vec{ex}×\vec{es}}{\vec{ex}×\vec{ey}} - 1 & 0 & 1 
\end{bmatrix}

/**
 * (0, 0)を始点、(1, 1)を終点とする正方形に対し4頂点を任意座標に配置できる行列を設定する
 * @param mat 計算結果の出力先の行列
 * @param sx 始点のX座標
 * @param sy 始点のY座標
 * @param xx 右上の点のX座標
 * @param xy 右上の点のY座標
 * @param yx 左下の点のX座標
 * @param yy 左下の点のY座標
 * @param ex 終点のX座標
 * @param ey 終点のY座標
 */
function setDeformation(mat, sx, sy, xx, xy, yx, yy, ex, ey) {
    // 単位行列を設定
    setIdentity(mat);

    // 始点の座標を設定する行列を掛ける
    mulMatrix(
        mat,
        1, 0, 0, sx,
        0, 1, 0, sy,
        0, 0, 0, 0,
        0, 0, 0, 1);

    // 右上の点、左下の点の座標を設定する行列を掛ける
    mulMatrix(
        dst,
        xx - sx, yx - sx, 0, 0,
        xy - sy, yy - sy, 0, 0,
        0, 0, 0, 0,
        0, 0, 0, 1);

    // 終点の座標を設定する行列を掛ける
    let exx = xx - ex; // x - e
    let exy = xy - ey;
    let eyx = yx - ex; // y - e
    let eyy = yy - ey;
    let esx = sx - ex; // s - e
    let esy = sy - ey;

    // (x - e) × (y - e) 終点、点X、点Yの三角形の面積
    let det = exx * eyy - exy * eyx; 
    // (x - e) × (s - e) / ((x - e) × (y - e)) 始点、終点、点Xの三角形と終点、点X、点Yの面積比
    let dx = (exx * esy - exy * esx) / det; 
    // (s - e) × (y - e) / ((x - e) × (y - e)) 始点、終点、点Yの三角形と終点、点X、点Yの面積比
    let dy = (esx * eyy - esy * eyx) / det;

    mulMatrix(
        dst,
        dy, 0, 0, 0,
        0, dx, 0, 0,
        0, 0, 0, 0,
        dy - 1, dx - 1, 0, 1);
}

 注意

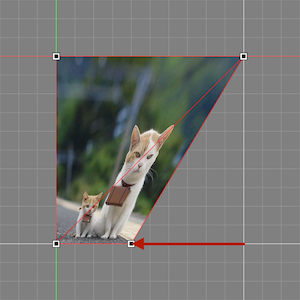
この行列による矩形の自由変形の実装は完全に万能というわけでもなく、ある特定の頂点の配置の仕方をすると計算が破綻することがあります。例えば頂点の内角のいずれかが180°を超えたり、辺と辺がクロスするように頂点を配置すると計算が破綻し変な場所に画像が表示されてしまうので、そこは注意点となります。
failure1.png failure2.png

成果物

使い方

各頂点をドラッグして移動、頂点以外をドラックした場合は全体移動します。

ライセンス

MIT Licence です。コピー、改変はご自由にどうぞ。

18
11
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
18
11