using System;
using System.Collections;
using System.Collections.Generic;
using System.Linq;
using UnityEngine;
using UnityEngine.UI;
using UnityEditor;
/// <summary>
/// カードを複数配置する際のLayoutGroup
/// </summary>
/// <remarks>
/// ヒエラルキー上で座標を同定するのが目的であり、Play中は重いので使わない
/// </remarks>
public class CardLayoutGroup : LayoutGroup
{
/// <summary>
/// 配置方法のパターン
/// </summary>
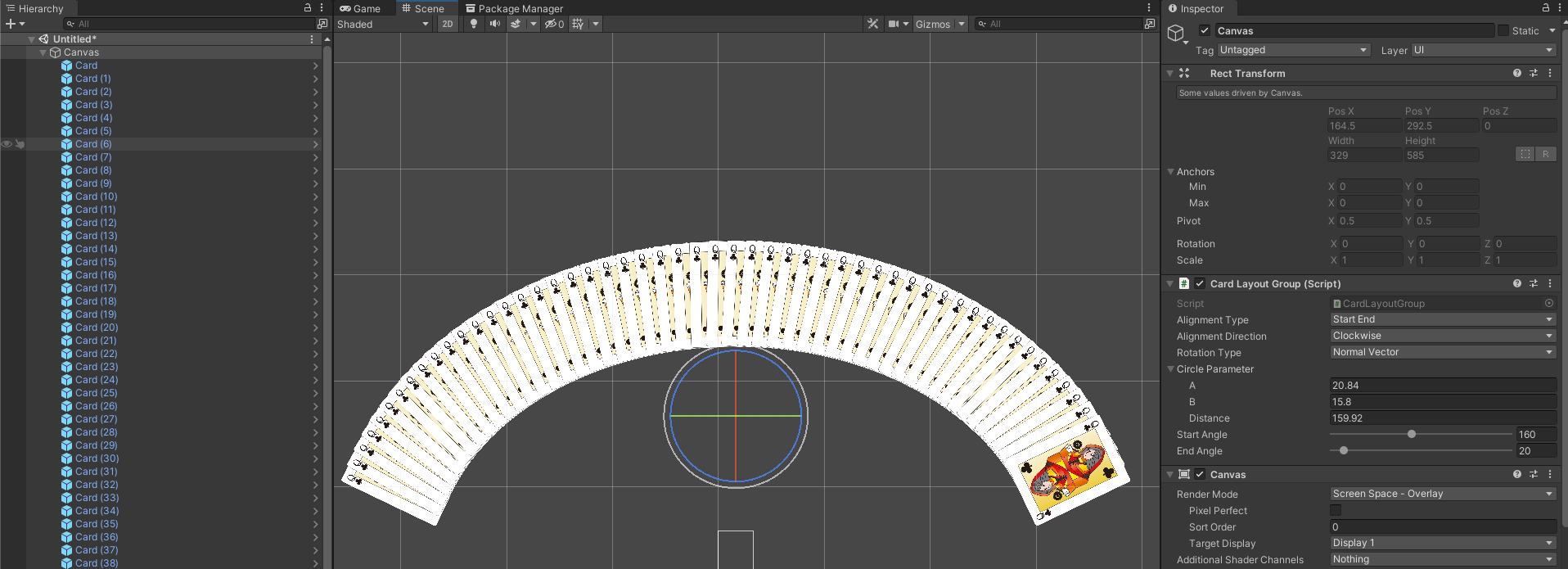
public enum AlignmentType
{
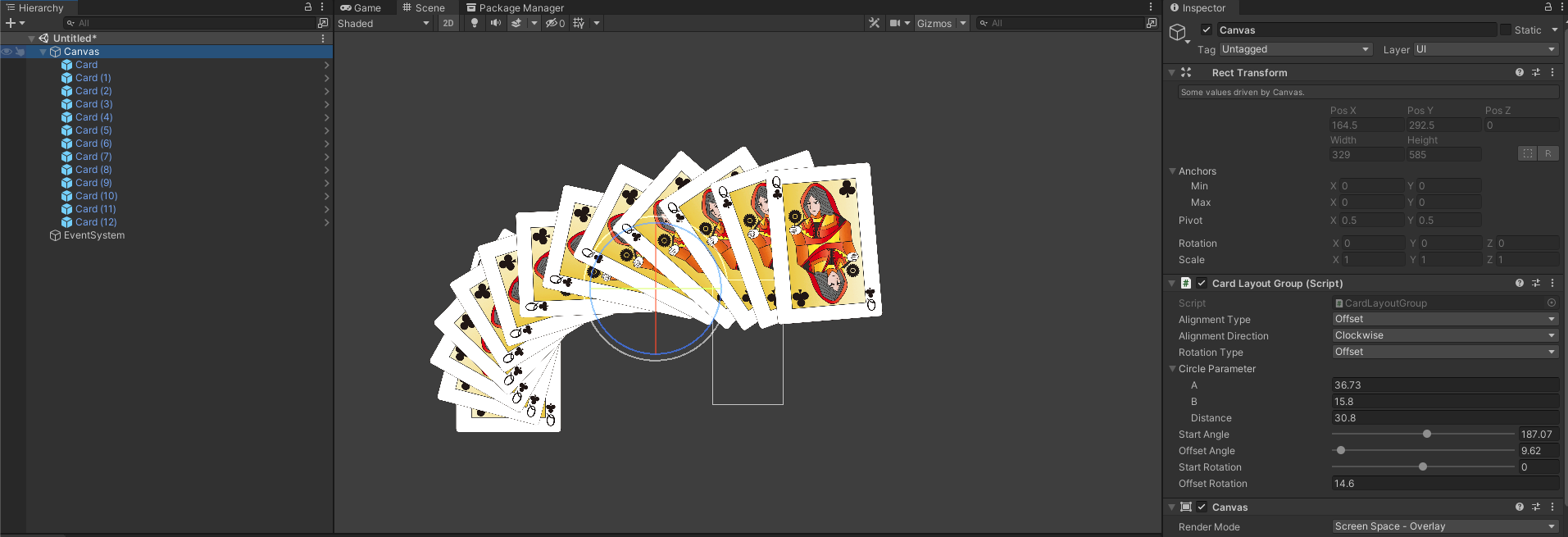
Offset, // 始点から順にOffsetAngleごとに等間隔で配置
StartEnd // 始点角度/終点角度を指定して、その中で按分された楕円上の座標に配置
}
/// <summary>
/// オブジェクトのRotationを変更する方法
/// </summary>
public enum RotationType
{
None, // オブジェクトのRotationは変更しない
NormalVector, // 法線ベクトル方向にRotationを変更
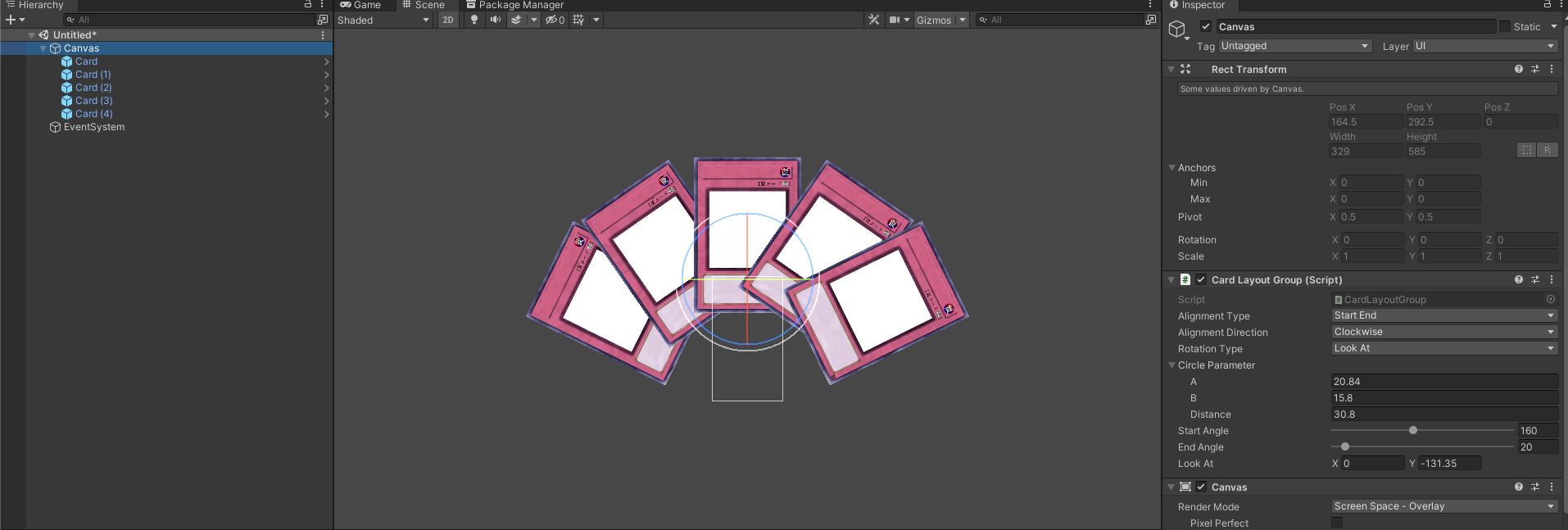
LookAt, // 要素のY座標下側が特定の座標を向くように変更
Offset, // 要素数に応じて特定の角度ずつRotationを変更
StartEnd // 始点Rotation/終点Rotationを指定して按分された角度で回転
}
/// <summary>
/// 要素の配置方向
/// </summary>
public enum Direction
{
Clockwise, // 時計回り
CounterClockwise // 反時計回り
}
/// <summary>
/// 楕円方程式を再現するためのパラメータ
/// </summary>
[Serializable]
private class CircleParameter
{
/// <summary>
/// 楕円方程式 x^2/a^2 + y^2/b^2 = 1のaの値
/// </summary>
[SerializeField]
private float a;
public float A { get => this.a; }
/// <summary>
/// 楕円方程式 x^2/a^2 + y^2/b^2 = 1のbの値
/// </summary>
[SerializeField]
private float b;
public float B { get => this.b; }
/// <summary>
/// 媒介変数座標(acosθ, bsinθ)にかける中心からの距離
/// </summary>
[SerializeField]
private float distance;
public float Distance { get => this.distance; }
}
[SerializeField]
private AlignmentType alignmentType;
public AlignmentType Alignment { get => this.alignmentType; }
[SerializeField]
private Direction alignmentDirection;
[SerializeField]
private RotationType rotationType;
public RotationType Rotation { get => this.rotationType; }
[SerializeField]
private CircleParameter circleParameter;
/// <summary>
/// 要素を配置する際の始点のオイラー角
/// </summary>
[SerializeField]
[Range(0f, 360f)]
private float startAngle;
/// <summary>
/// 要素を配置する際のオイラー角の差分
/// </summary>
[SerializeField]
[Range(0f, 360f)]
[HideInInspector]
private float offsetAngle;
/// <summary>
/// 要素を配置する際の終点のオイラー角
/// </summary>
[SerializeField]
[Range(0f, 360f)]
[HideInInspector]
private float endAngle;
/// <summary>
/// 配置された要素のRotationを向かせる方向
/// </summary>
[SerializeField]
[HideInInspector]
private Vector2 lookAt;
/// <summary>
/// 要素を回転させる場合のRotationの始点
/// </summary>
[SerializeField]
[HideInInspector]
[Range(-180f, 180f)]
private float startRotation;
/// <summary>
/// 要素を回転させる場合のRotationの差分
/// </summary>
[SerializeField]
[HideInInspector]
private float offsetRotation;
/// <summary>
/// 要素を回転させる場合のRotationの終点
/// </summary>
[SerializeField]
[HideInInspector]
[Range(-180f, 180f)]
private float endRotation;
private void Calclate()
{
m_Tracker.Clear();
var childs = this.transform.GetComponentsInChildren<RectTransform>()
.Where(x => this.gameObject != x.gameObject)
.Where(x => x.gameObject.activeSelf)
.ToList();
var childCount = childs.Count;
if (childCount == 0) return;
for (int i = 0; i < childCount; i++)
{
var child = childs[i];
m_Tracker.Add(this, child, DrivenTransformProperties.Anchors | DrivenTransformProperties.AnchoredPosition | DrivenTransformProperties.Pivot);
// 要素数に対する按分
var divide = (childCount > 1) ? (float)i / (float)(childCount - 1) : 0.0f;
// 配置開始位置からのoffsetを計算
var deltaAngle = this.alignmentType switch
{
AlignmentType.Offset => i * this.offsetAngle,
AlignmentType.StartEnd => Math.Abs(this.endAngle - this.startAngle) * divide,
};
// 要素n個目のオイラー角
var nAngle = this.startAngle + (this.alignmentDirection == Direction.Clockwise ? -deltaAngle : deltaAngle);
// 楕円状の座標 (acosθ, bsinθ)
var nPosition = new Vector2(this.circleParameter.A * Mathf.Cos(nAngle * Mathf.Deg2Rad), this.circleParameter.B * Mathf.Sin(nAngle * Mathf.Deg2Rad));
child.anchoredPosition = nPosition * this.circleParameter.Distance;
switch (this.rotationType)
{
case RotationType.None:
// オブジェクトの回転を行わない
child.rotation = Quaternion.identity;
break;
case RotationType.NormalVector:
// 楕円上の点の法線ベクトルは(bcosθ, asinθ)
var normalVector = new Vector2(this.circleParameter.B * Mathf.Cos(nAngle * Mathf.Deg2Rad), this.circleParameter.A * Mathf.Sin(nAngle * Mathf.Deg2Rad));
child.rotation = Quaternion.AngleAxis(Mathf.Atan2(normalVector.x, normalVector.y) * Mathf.Rad2Deg, Vector3.back);
break;
case RotationType.LookAt:
// カードのY座標下部を基準に回転させる
var lookVector = child.anchoredPosition - this.lookAt;
child.rotation = Quaternion.AngleAxis(Mathf.Atan2(lookVector.x, lookVector.y) * Mathf.Rad2Deg, Vector3.back);
break;
case RotationType.Offset:
// Rotationは左回転が正
var deltaRotation = i * this.offsetRotation;
child.rotation = Quaternion.Euler(0, 0, this.startRotation - deltaRotation);
break;
case RotationType.StartEnd:
// 按分でQuaternionを算出
child.rotation = Quaternion.Lerp(Quaternion.Euler(0, 0, this.startRotation), Quaternion.Euler(0, 0, this.endRotation), divide);
break;
}
child.anchorMin = child.anchorMax = child.pivot = new Vector2(0.5f, 0.5f);
}
}
protected override void OnEnable() { base.OnEnable(); Calclate(); }
public override void SetLayoutHorizontal()
{
}
public override void SetLayoutVertical()
{
}
public override void CalculateLayoutInputVertical()
{
Calclate();
}
public override void CalculateLayoutInputHorizontal()
{
Calclate();
}
#if UNITY_EDITOR
protected override void OnValidate()
{
base.OnValidate();
Calclate();
}
#endif
}
#if UNITY_EDITOR
[CustomEditor(typeof(CardLayoutGroup))]
public class CardLayoutGroupEditor : Editor
{
private CardLayoutGroup _target;
private SerializedProperty offsetAngle;
private SerializedProperty endAngle;
private SerializedProperty lookAt;
private SerializedProperty startRotation;
private SerializedProperty offsetRotation;
private SerializedProperty endRotation;
private void OnEnable()
{
_target = target as CardLayoutGroup;
this.offsetAngle = serializedObject.FindProperty("offsetAngle");
this.endAngle = serializedObject.FindProperty("endAngle");
this.lookAt = serializedObject.FindProperty("lookAt");
this.startRotation = serializedObject.FindProperty("startRotation");
this.offsetRotation = serializedObject.FindProperty("offsetRotation");
this.endRotation = serializedObject.FindProperty("endRotation");
}
public override void OnInspectorGUI()
{
this.serializedObject.UpdateIfRequiredOrScript();
var iterator = this.serializedObject.GetIterator();
for (var enterChildren = true; iterator.NextVisible(enterChildren); enterChildren = false)
{
if (iterator.propertyPath == "m_Padding" || iterator.propertyPath == "m_ChildAlignment") continue;
using (new EditorGUI.DisabledScope(iterator.propertyPath == "m_Script"))
{
EditorGUILayout.PropertyField(iterator, true);
}
}
switch(_target.Alignment)
{
case CardLayoutGroup.AlignmentType.Offset:
EditorGUILayout.PropertyField(this.offsetAngle);
break;
case CardLayoutGroup.AlignmentType.StartEnd:
EditorGUILayout.PropertyField(this.endAngle);
break;
}
switch(_target.Rotation)
{
case CardLayoutGroup.RotationType.LookAt:
EditorGUILayout.PropertyField(this.lookAt);
break;
case CardLayoutGroup.RotationType.Offset:
EditorGUILayout.PropertyField(this.startRotation);
EditorGUILayout.PropertyField(this.offsetRotation);
break;
case CardLayoutGroup.RotationType.StartEnd:
EditorGUILayout.PropertyField(this.startRotation);
EditorGUILayout.PropertyField(this.endRotation);
break;
}
serializedObject.ApplyModifiedProperties();
}
}
#endif