フレームワーク任せにせず、バックプロパゲーションを理解しておきたい理由 (原題:Yes you should understand backprop)

#訳注
ディープラーニングを理解するためには数学が必要、バックプロパゲーションは理解していなくてはならない。という話はよく聞くが、何故理解しておきべきだという事はあまり書かれない。
.back()すれば自動的に計算してくれるし頭いい人が実装してくれるじゃん。。と言われると確かにそうだなあ。と思う。

TeslaのAI責任者であるKarpahyのブログ記事がこの疑問への答えを実例を踏まえて解説していたので和訳を提供する。

始めに

スタンフォードでディープラーニングの授業CS231nを提供したとき、プログラム課題には学生は自分でバックプロパゲーションを一番低いレベルで実装するように設計した。学生はネットワークのフォワードパスとバックワードパスをそれぞれnumpyを使い実装する必要があった。想定どおり、複数の学生が掲示板でこのような文句を寄せた。

ディープラーニングフレームワーク(Tensorflowなど)は自動的に逆伝搬を計算してくれるのに何故バックプロパゲーションを実装しなければならないの？

これは実に理にかなった主張に見えるー実世界で逆伝搬処理を書く必要がないならば、何故実装する練習をしなければいけないのか？我々はいたずらに学生をいじめているのか？この質問へのよく見る回答として「フレームワークの動作原理を理解しておく事は知識として重要」または「自分でコアアルゴリズムを今後直したいかもしれないから」などがある。しかし、ここでは本記事を書くに至った強く実用的な主張を展開したい。

バックプロパゲーションは不十分な抽象表現に過ぎない。
The problem with Backpropagation is that it is a leaky abstraction.

過度な抽象化によって簡単にディープラーニングの学習の罠にハマってしまうー様々なレイヤーを単純に積み重ねるだけでバックプロパゲーションが魔法のように素敵なモデルを構築してくれるといつでもなるわけではない。
それではいくつかの実例でこの魔法が働かない例を見てみよう。

#シグモイド関数における勾配消失
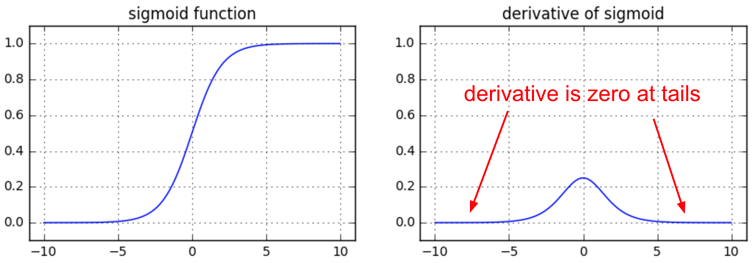
それでは単純な例から見ていこう。昔はシグモイド関数やtanhを全結合層で使うことが流行っていた。ここで逆伝搬を意識していない人がよく陥る罠は、もし重みの初期化やデータ前処理注意して行わないとこのような非線形関数は飽和し学習自体を止めてしまうー学習ロスがフラットになり下げ止まってしまうのだ。例えばこの処理はnumpyで以下のように書ける。

z = 1/(1 + np.exp(-np.dot(W, x))) # forward pass
dx = np.dot(W.T, z*(1-z)) # backward pass: local gradient for x
dW = np.outer(z*(1-z), x) # backward pass: local gradient for W

もし重み行列Wが大きい数に初期化されているとmatrix multiplyの出力レンジはとても広くなり(e.g. -400~400)、出力ベクトルzはほとんどバイナリ出力となってしまう(0か1しか取らない)。このようなケースではz*(1-z)、つまりシグモイド関数のローカル勾配はどのようなケースでもゼロ(消失)となってしまい、xとw両方の勾配もまたゼロになってしまう。また残りの逆伝搬もチェインルールにより全てこの時点からゼロとなってしまうことにも注意したい。

他に興味深い情報としてシグモイドのローカル勾配z(1-z)はz=0.5の時、最大値0.25をとる。これはつまりシグモイドを通るたびに勾配信号は最低でも1/4に減衰してしまう(時にはもっと)事を示している。もしsgdでネットワークを学習しているならば、そのためあなたの浅い層のレイヤは高層のものより(深い層より)ずっと遅く学習が進むことになるだろう。

TLDR

もしあなたがシグモイドやtanhを使っていてバックプロパゲーションを理解しているのならば、それらが飽和しないような初期化をちゃんとかけられているか注意するべきである。この事はcs231のビデオでも触れられているから観てね。
https://youtu.be/gYpoJMlgyXA?t=14m14s

死にゆくReLU

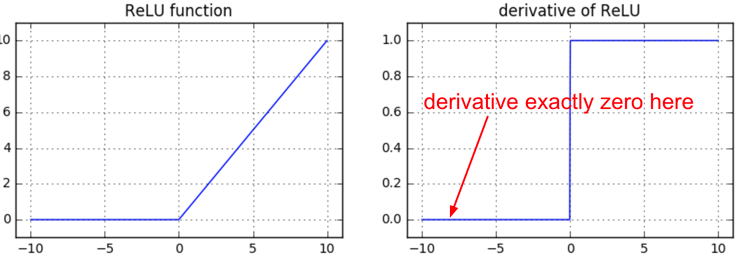
もう一つの楽しい非線形関数はReLUであり、それはゼロ以下の出力をシャットアウトする。ReLUを使う全結合層の順、逆伝搬はこのような記述を含む。

z = np.maximum(0, np.dot(W, x)) # forward pass
dW = np.outer(z > 0, x) # backward pass: local gradient for W

この記述をしばらく眺めると、もしニューロンが順伝搬時にゼロ以下が入力され出力がゼロに固定(クランプ)されると(z=0つまり発火しない)、それらの重みはゼロ勾配が与えられてしまうことがわかる。これが所謂“死んだReLU”問題を引き起こしてしまう。つまりもしreluニューロンが発火しないように初期化されてしまうと、または大きな値でアップデートされこのような状態に陥ってしまうとそのニューロンは永久に“死んで”しまう。まるで治ることのない脳損傷のように。時に順伝搬を試すとあなたのネットワークのほとんどの部分が(40%)が発火せず常にゼロを出力しているのを確認することができるだろう。(訳注:この問題を避けるために負でもゼロを取らないleaky reluが最近使われてきたのだろう)

TLDR

もしあなたがバックプロパゲーションを理解しネットワークがReLUを持つならば、いつも死んだReLUについて気にするべきだ。このようなニューロンはデータセット全体を走らせても一度も発火しない。またアグレッシブに学習率を変える事で途中でReLUが死ぬこともある。

#RNNにおける勾配爆発
バニラRNNでは多くの想定していないバックプロぱゲーションの効果を見ることができる。授業スライドからシンプルなRNNを引用する;入力を受けずに隠れ状態の循環のみ計算する(入力xは常にゼロで良い)。

このRNNをT時間分展開する。そして逆伝搬の処理を注意深く見てみると、勾配信号は全ての隠れ層を通り時間を遡っていき(going backwards in time)常に同じ行列で掛け合わされていく(行列whh)。

ある数値aに対して何度も数値bを掛け合わせるとどうなる(i.e. abbbbbb…)?
もしbが1より小さいならばゼロになり、bが1より大きいならば無限に爆発してしまう。同様のことがRNNの逆伝搬でも起こってしまう、ただbは行列のためその固有値に関して考慮する必要がある。

TLDR

もしあなたがバックプロパゲーションを理解しRNNを使っているなら勾配クリッピングをするかLSTMを使う必要がある。

Spotted in the Wild: DQN Clipping

もう一つ見てみようーこれが本記事を書く動機を与えてくれた。昨日他の研究者がどのようにDeepQ学習をTensorFlowでインプリしているか知りたくて調べていた。どやってQ[:,a]を実装しているのか、ここでaはinteger vectorでこの動作はtensorflowでサポートされていなかった。以下が見つけたインプリだ。

もしDQNに親しんでいたら target_q_tがあり、それは単に[reward * \gamma \argmax_a Q(s’,a)]であることがわかる。またq_acted, つまりQ(s,a)がある。著者は二つを変数デルタに差分を取り、これを行295のL2ロスにより最小化したい。これは良い。

問題は行291だ。著者らは例外に対し頑強にするため、デルタが大きい時はクリッピングをするようにしている。これは順伝搬時を考えると正しいのだが、逆伝搬時に重要なバグがある。クリッピング関数はレンジmin,maxを超えると勾配がゼロとなってしまい想定される動作から外れてしまう！qデルタをそのままクリッピングし逆伝搬も正しく実装したい場合はHuberロスを使うのが良い。
tfで書くとごちゃっとしているが、torchならもっとシンプルにかけるよ。

def clipped_error(x): 
  return tf.select(tf.abs(x) < 1.0, 
                   0.5 * tf.square(x), 
                   tf.abs(x) - 0.5) # condition, true, false

まとめ

バックプロパゲーションは不完全な抽象化に過ぎない;
もしあなたが“TensorFlowが勝手にやってくれるから”と理解を放棄してしまったら、バックプロパゲーションが引き起こす危険な事態に対処する用意ができていないかもしれない。理解が未熟だとニューラルネットをデバッグや実装するのに効率的な手段を取れないであろう。

良いニュースはバックプロパゲーションを理解するのは難しくないと言う点だ。(もしちゃんとプレゼンされたならだけど！)
自分は世の中のバックプロパゲーション説明資料の95%は間違えてプレゼンしている(ページ全体を数式で覆っていて)と強く思っている。自分はCS231nの講義でバックプロパゲーションを学ぶことをオススメする、何故ならば数式よりもどう動作するかなど直感を重要視して説明しているからだ(手前味噌でゴメンネ)。また授業課題を通し自分でバックプロパゲーションを記述することで理解も深まるだろう(訳注:ゼロから作るディープラーニングはcs231をモデルとしているので日本語でサンプルコード付きでバックプロパゲーション実装が学べていいですネ！)

これで終わりだ！この記事を読んだことでバックプロパゲーションにより注意深くなりどう動作しているか理解を深めてくれればと思う。また不覚にもCS231の宣伝ばかりしてごめんね！