前の記事で少し画像処理を齧って面白かったので、今回は論文を読んで簡単な画像処理を実装してみました。
(以下の画像の様な感じです。)
| src | dst |
|---|---|
 |
 |
今回読んだ論文は割と古め(2004年)でそこまで実装自体は難しそうではなかったのでやってみました。(ただ、論文に掲載されている結果ほどうまく行っていません・・・)
今回のソースコードはgithubに上げてあります。
https://github.com/aratakokubun/GraphBasedSegmentationWithUnionFind.git
画像処理の概要
今回実装したのは画像領域分割の処理で、輝度
結合の条件として、近傍の画素との境界(Edge)を小さい順番に判定して次々と領域を結合していきます。
アルゴリズム
以下の1-5を実行し、結果として独立したComponentのリストを得ます。このComponentが画素同士が結合された領域になります。
- 各画素の8近傍(grid)もしくは一定距離内(nearest-neighbor)の画素との境界(Edge)を全て抽出する。
初期状態では全ての画素が結合されていない状態であり、この各要素をComponentとして扱う。 - 各画素に関して、結合の基準として用いる値を計算する。
例えば、今回の場合は輝度値(luminance)を用いており、輝度の近い画素同士を同じ領域として結合する。 - 抽出した各Edgeの差(diff)を計し、diff値の小さい順にソートする。
- ステップ5をEdgeの小さい順に繰り返す
- Edgeの値が、境界の両側のComponentの内部差(MInt)より小さい場合、2つのComponentを結合して1つのComponentとする。
※ このステップはEdgeの結合条件で詳細を記載します。
Edgeの結合条件
ステップ5の結合に関して、Edgeの差diffと、2つのComponent C1, C2の内部差Mintに関して、以下の条件の場合に結合します。
diff <= MInt(C1, C2)
2つのComponentの内部差Mintは以下の様に定義します。
MInt(C1, C2) = min(Int(C1)+τ(C1), Int(C2)+τ(C2))
各Componentの内部差Intは、Componentに今までに結合された境界の最大値をとります。Componentが1画素要素の場合は0になります。(ただし、この記述は厳密には正しくないので、詳しく知りたい方は参考文献1を参照してください。)
また、τはComponentのサイズに応じた境界値関数で、以下の様に定義されます。
τ(C) = k/|C|
kは定数のパラメータで、kが大きいほどEdgeの結合が起きやすく、結果のComponentが大きくなりやすいです。
高速化のためのテクニック
処理を高速化するためにUnion-Findというアルゴリズムを用います。
Union-Findでは集合Sに対して互いに素なSの部分集合を考えます。今回の画像領域分割の処理では、集合Sが画素の集合である画像、部分集合がComponentに該当します。
これをDisjointSetと言い、union, findの操作を以下の様に定義します。
- union(C1, C2)
部分集合C1, C2を合併し、新たにC1とする。(Componentを結合するステップ5の処理に該当します。) - find(a)
要素a(画素)が属する部分集合を取得する。
このunion処理の際、各Componentの代表となる要素を1つずつ定義しておき、結合される側(C2)の各要素から結合する側(C1)の代表の要素へリンクを張る様にすることで1つの配列で簡易に処理が実装できます。
また、TreeによるUion-Findを利用することでさらに高速化が可能になります。
実装方法はここでは細かく記載しませんが、Union-Findに関してはかなり詳細な解説が参考文献2に記載されていますので、是非ご参照ください。また、参考文献3では計算量などの解説もありますので、併せてご参照ください。
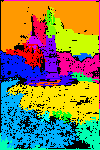
結果
今回pythonで実装した結果が以下になります。
全ての領域ではなく、領域サイズの大きい上位40を色付けしています。
| src | dst |
|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
今回のソースコードはgithubに上げてあります。
https://github.com/aratakokubun/GraphBasedSegmentationWithUnionFind.git
参考文献
- Efficient Graph-Based Image Segmentation
http://cs.brown.edu/~pff/papers/seg-ijcv.pdf - Union Findの実装
http://www.geocities.jp/m_hiroi/light/pyalgo61.html - Disjoint-Set Data Structures
http://ocw.mit.edu/courses/electrical-engineering-and-computer-science/6-046j-design-and-analysis-of-algorithms-spring-2012/lecture-notes/MIT6_046JS12_lec16.pdf