Hello, World! あーみーです.
この記事はLife is Tech! Tokai Mentors Advent Calendar 2018 1日目の記事です.今日から頑張っていきましょう.
はじめに
この記事ではコンピュータの世界で扱われる2進法を簡単な定義から色々な分野の話まで持っていこうと思います.
今回は論理演算を論理回路図とともに触れて,半加算器,全加算器で2進法の加算をします.
2進法とは
普段私達が日常で使っているのは10進法です.10進法では0~9までの10個の数字を使用します.そして0~9まで10個数えたら次の位に桁を上げて数を表現していきます.10進法で表された数字のことを10進数と呼びます.
00 -> 01 -> 02 -> 03 -> 04 -> 05 -> 06 -> 07 -> 08 -> 09 -> 10 -> ...
この場合だと「十の位」が0から1に上がっているのがわかります.(もちろん百の位,千の位,...は省略してあります.)
10進法では10個の数字を使用しましたが,2進法では「0」と「1」の2個の数字を使用します.そして0~1まで2個数えたら次の位に桁を上げて数を表現していきます.2進法で表された数字のことを2進数と呼びます.
0000 -> 0001 -> 0010 -> 0011 -> 0100 -> 0101 -> 0110 -> 0111 -> 1000 -> ...
10進法では10個数えたときに桁が上がりその位のことを「十の位」と呼びました.2進法でも同じように数えると,それぞれ右の桁から「一の位」「二の位」「四の位」「八の位」とここでは呼びます.
2進法,10進法どちらも桁上りする位が冪乗であることに気が付きます.面白いですね.
10進数を2進数へ変換
10進数を2進数に変換をしたい時は,その数字を2で割っていき余りを逆から読めば変換することができます.
例えば10進数の「11」を2進数に変換したい時,
\begin{align}
11\div2=5\cdots1\\
5\div2=2\cdots1\\
2\div2=1\cdots0\\
1\div2=0\cdots1
\end{align}
商が0になるまで割っていき逆から読むと「1011」となります.これが10進数の「11」を2進数で表した表記です.
2進数を10進数へ変換
逆に2進数を10進数に変換したい時は,桁の位の数に2進数で表された数字を重みとしてかけて総和を取ると変換することができます.
例えば先程の2進数の「1011」を10進数に変換したい時,
2^3\times1\quad+\quad2^2\times0\quad+\quad 2^1\times1\quad+\quad2^0\times1\\
「八の位」「二の位」「一の位」に重みとして1がかかっているので足し合わせると「11」となります.
論理演算
コンピュータは2進法で動いているというのはよく知られた話で,そのアーキテクチャの性質上電圧の高低などの2値で表現ができるからです.
さて,普段私達が日常で使っている基本的な演算は四則演算です.コンピュータの世界にも「論理演算」と呼ばれる演算があります.これは「0」と「1」だけで演算をします.種類としては「AND演算」「OR演算」「XOR演算」「NOT演算」の4種類があります.入力にx,yの値を取り,「0」または「1」の値を出力します.以下の表が4種類の演算結果です.
| x | y | x AND y | x OR y | x XOR y |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 |
| 0 | 1 | 0 | 1 | 1 |
| 1 | 0 | 0 | 1 | 1 |
| 1 | 1 | 1 | 1 | 0 |
| x | NOT x |
|---|---|
| 0 | 1 |
| 1 | 0 |
これはプログラムのif文の条件部も同じ概念です.「0」をFalse,「1」をTrueとすると,論理演算の出力がわかります.
# status1とstatus2が共にTrueの時do_something()が実行される
if status1 and status2:
do_something()
この4種類の論理演算は以下の論理回路図としても表されます.論理回路図は左側からx,yの入力を得て,右側へ結果を出力します.
2進数の加算
手計算の場合
2進数の加算を手計算で行う場合は筆算でやるのが簡単だと思います.
例えば10進数の「3」と「2」の足算を2進数で行う場合
{\Large{
\begin{array}{rr}
& 11 \\
+ & 10 \\ \hline
&101
\end{array}
}} \\
「二の位」が桁上りをして「101」となります.この数字を10進数に変換してみると,
2^2\times1\quad+\quad 2^1\times0\quad+\quad2^0\times1\\
「5」であるため,加算の結果は正しいです.
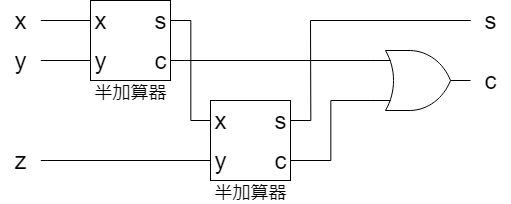
半加算器
コンピュータで2進数の加算をする場合はまずは半加算器という論理回路を使用します.以下の論理回路図が半加算器です.
この論理回路図の演算結果が以下の表になります.また,初めて見る人には複雑な論理回路図であるため,論理演算が行いやすいように,p地点とNOT c地点の演算結果も載せています.
|x|y||c|NOT c|p|s|出力結果cs|
|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|:-:|
|0|0||0|1|0|0|00|
|0|1||0|1|1|1|01|
|1|0||0|1|1|1|01|
|1|1||1|0|1|0|10|
入力にx,yを入れると出力「c,s」に結果が出てきます.半加算器では一桁と一桁の加算ができます.
sの結果を見て気がつく人もいると思いますが,sはXOR演算の結果と同じになっています.そのため,半加算器はAND回路とXOR回路でも実現ができます.
全加算器
半加算器だけでは,一桁と一桁の加算しかできませんでしたが,複数桁と複数桁の加算をするためには全加算器を使用します.以下の図が全加算器です.
全加算器には半加算器を2つ使います.zには下位の桁上げ出力を入力します.
この論理回路図の演算結果が以下の表になります.
| x | y | z | c | s | 出力結果cs | |
|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 00 | |
| 0 | 0 | 1 | 0 | 1 | 01 | |
| 0 | 1 | 0 | 0 | 1 | 01 | |
| 0 | 1 | 1 | 1 | 0 | 10 | |
| 1 | 0 | 0 | 0 | 1 | 01 | |
| 1 | 0 | 1 | 1 | 0 | 10 | |
| 1 | 1 | 0 | 1 | 0 | 10 | |
| 1 | 1 | 1 | 1 | 1 | 11 |
論理回路の場合
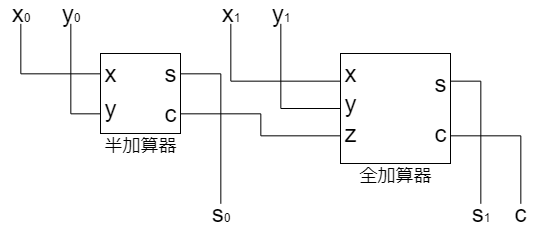
最下位桁用の半加算器とその桁上り出力cを全加算器のzと繋ぐと二桁と二桁の加算が可能になります.
以下の図が二桁と二桁の加算が可能な論理回路になります.$x_1x_0$と$y_1y_0$の加算が可能です.
また,演算結果が以下の表になります.
| $x_1$ | $x_0$ | $y_1$ | $y_0$ | $s_0$ | $s_1$ | c | $出力結果cs_1s_0$ | |
|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 000 | |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 001 | |
| 0 | 0 | 1 | 0 | 0 | 1 | 0 | 010 | |
| 0 | 0 | 1 | 1 | 1 | 1 | 0 | 011 | |
| 0 | 1 | 0 | 0 | 1 | 0 | 0 | 001 | |
| 0 | 1 | 0 | 1 | 0 | 1 | 0 | 010 | |
| 0 | 1 | 1 | 0 | 1 | 1 | 0 | 011 | |
| 0 | 1 | 1 | 1 | 0 | 0 | 1 | 100 | |
| 1 | 0 | 0 | 0 | 0 | 1 | 0 | 010 | |
| 1 | 0 | 0 | 1 | 1 | 1 | 0 | 011 | |
| 1 | 0 | 1 | 0 | 0 | 0 | 1 | 100 | |
| 1 | 0 | 1 | 1 | 1 | 0 | 1 | 101 | |
| 1 | 1 | 0 | 0 | 1 | 1 | 0 | 011 | |
| 1 | 1 | 0 | 1 | 0 | 0 | 1 | 100 | |
| 1 | 1 | 1 | 0 | 1 | 0 | 1 | 101 | |
| 1 | 1 | 1 | 1 | 0 | 1 | 1 | 110 |
二桁の2進数同士の加算なので,10進数だと「3+3=6」までとなります.
それ以上の桁を加算したい場合は最後の桁上り出力cを次の全加算器の入力zにどんどんつなげていけば良いだけです.
一見手計算のほうが簡単そうに見えますが,大きい数の計算や,膨大な量の計算を行う場合はコンピュータにやらせたほうがとても簡単です.しかも中身は単純な処理ですから.
終わりに
今日は2進法から始めて論理回路までを記事にしました.
「プログラマだからそんな低レイヤーなことうろ覚えでいい」ということはありません.プログラマだからこそコンピュータアーキテクチャと寄り添っていくべきです.
それでは,Happy Hacking! ![]()