こんにちは、arcadia13です。
15回目のMATLAB記事となる今回は、数値計算の手法の一つである「ルンゲ・クッタ法(古典的ルンゲ・クッタ法)」を説明します。
これはオイラー法を改良したもので、オイラー法で求めた近似解よりも真の解との誤差が小さくなります。
ここでは、広く用いられている「4次のルンゲ・クッタ法」を説明します。
実は、ode45() コマンドに使われているのがルンゲ・クッタ法です。
つまり、ルンゲ・クッタ法の実装は ode45() コマンドを自分で実装することだと思っていいです。
1. ルンゲクッタ法のアルゴリズム
ルンゲ・クッタ法のアルゴリズムは、14回で説明したオイラー法とほぼ同じです。ということで、まずはオイラー法のおさらい。
なお、オイラー法の詳細は14回をご覧ください。
オイラー法のアルゴリズム
-
微分方程式の初期値 $y_0=y(x_0)$ と、積分範囲 $a(=x_0) \leq x \leq b$ を決める。これによりオイラー法の出発点 $(x,y)=(x_0, y_0)$ が用意できる。
-
刻み幅 $h$ によって積分範囲を $n$ 分割する。すなわち $x_{k+1}=x_k + h\
(k=0,1,…,n−1), x_0=a, x_n=b$ である。 -
$y_k=y(x_k)$ とすると、$(x_k,y_k)$ を近似式 $y_{k+1}\approx y_k + hf(x_k,y_k)$ に代入して $y_{k+1}$ を求める。
-
3 の手順を $y_1$ から $y_n$ が求まるまで繰り返す。
では、オイラー法とルンゲ・クッタ法のどこが違うかというと、それは近似式です。
近似式 $y_{k+1}\approx y_k + hf(x_k,y_k)$ の $f(x_k, y_k)$ の部分を以下のように変更します。
ルンゲ・クッタ法における近似式
\begin{eqnarray}
y_{k+1} &\approx& y_k + h\cfrac{k_1 + 2k_2 + 2k_3 + k_4}{6}\\
k_1 &=& f(x_k,\ y_k)\\
k_2 &=& f(x_k + \frac{h}{2},\ y_k + \frac{h}{2}k_1)\\
k_3 &=& f(x_k + \frac{h}{2},\ y_k + \frac{h}{2}k_2)\\
k_4 &=& f(x_k + h,\ y_k + k_3)\\
\end{eqnarray}
見るのも嫌な状態になってないでしょうか...。
しかしよく見てください。やっていることは単純で、$f(x,y)$ に色々と代入して計算しているだけです。
代入して計算するという意味ではオイラー法と同じ事をしています。
実際、オイラー法も $(x_k, y_k)$ を $f(x,y)$ に代入して計算してましたよね。それに少し手を加えただけです。
後のアルゴリズムはオイラー法と全く同じ。オイラー法を実装できた時点でルンゲ・クッタ法の大半は実装できていたわけです。
2 ルンゲ・クッタ法の実装
それではルンゲ・クッタ法の実装に移ります。
せっかく(?)ルンゲ・クッタ法を実装するので、ここは私の好きな物理と絡めて運動方程式を解きましょう。
題材は高校物理の力学でお馴染みの「斜方投射」です。
簡単のために二次元平面上で運動を考えるとし、また空気抵抗は無視します。
平面の原点に置いた質点を、仰角 $45$ 度の方向へ打ち上げ、その軌道を描画してみます。
初速度は適当に $10\ \text{m/s}$ としました。
% 質点の斜方投射
clear; clc;
%% 物理パラメータと運動方程式の初期条件
% 手順1,2はここで行う
x0 = 0; y0 = 0; % 原点
g = 9.8; % 重力加速度
theta = (45/180)*pi; % 45度の方向へ投げる
v0 = 10; % 初速度 m/s
% 運動方程式の初期条件
Y0 = [y0; v0*sin(theta)];
% シミュレーション時間
h = 10^(-4); %刻み幅
t = 0:h:5;
%% 運動方程式を解いてボールの軌跡を描画
x = x0 + v0*cos(theta)*t;
y = ClassicalRungeKutta(@MotionEquation, t, Y0); % 近似解
yTrue = y0 + v0*sin(theta)*t - (g*t.^2)/2; % 真の解
plot(x, y(1,:), 'LineWidth', 1.3);
hold on
plot(x, yTrue, 'g--','LineWidth', 1.3)
title('斜方投射')
legend('質点の軌跡')
xlabel('x[m]')
ylabel('y[m]')
set(gca,'FontSize',13)
ylim([0 5])
grid on
%% 斜方投射(鉛直上向き)の運動方程式
function Ydot = MotionEquation(t, Y)
g = 9.8;
nrow = length(Y);
Ydot = zeros(nrow, 1);
Ydot(1,1) = Y(2);
Ydot(2,1) = -g;
end
%% ルンゲ・クッタ法
function Yout = ClassicalRungeKutta(func, t, Y0)
% func:微分方程式の関数ハンドル
% t:積分範囲(hで分割済み)
% Y0:初期値
nrow = length(Y0);
ncol = length(t);
Y = zeros(nrow, ncol);
Y(:,1) = Y0; % 初期値の代入
h = t(2) - t(1); % 刻み幅
% 手順3,4
for k = 1:ncol-1
k1 = feval(func, t(k), Y(:,k));
k2 = feval(func, t(k) + h/2, Y(:,k) + h*k1/2);
k3 = feval(func, t(k) + h/2, Y(:,k) + h*k2/2);
k4 = feval(func, t(k) +h, Y(:,k) + h*k3);
Y(:, k+1) = Y(:, k) + h*(k1 + 2*k2 + 2*k3 + k4)/6;
end
Yout = Y;
end
なお、for文の中身はこのように書くこともできます(@WolfMoon 様のコードを参考にいたしました)。
k1 = func(t(k), Y(:,k));
k2 = func(t(k) + h/2, Y(:,k) + h*k1/2);
k3 = func(t(k) + h/2, Y(:,k) + h*k2/2);
k4 = func(t(k) +h, Y(:,k) + h*k3);
Y(:, k+1) = Y(:, k) + h*(k1 + 2*k2 + 2*k3 + k4)/6;
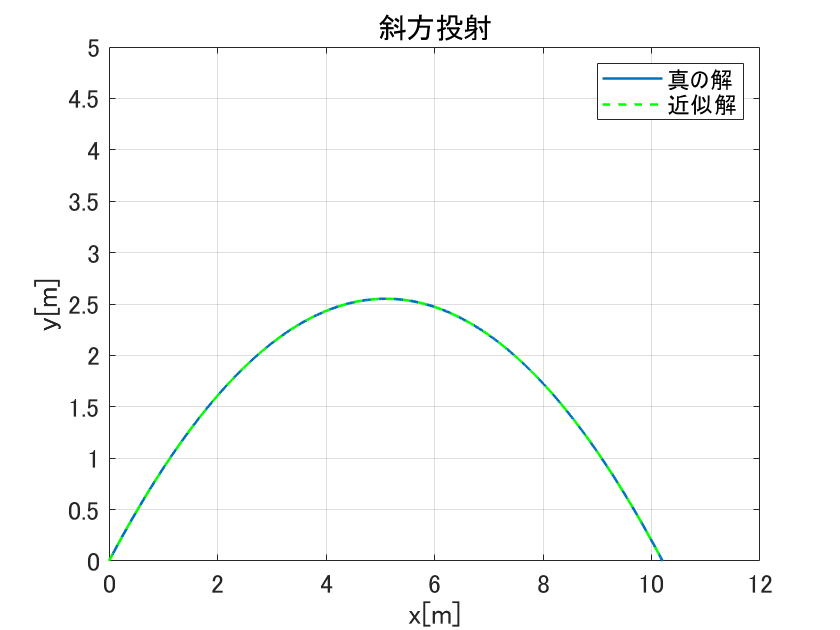
空気抵抗を無視した斜方投射には、高校物理の教科書にも掲載されているような、有名な公式(真の解)が存在します。
ちょうどいいので近似解と公式の軌跡を比較してみました。
題材が簡単とはいえ、完全一致していますね。素晴らしい。
本記事のメインは以上で終了です。
※ ルンゲ・クッタ法の深堀りを促すおまけ
ルンゲ・クッタ法のアルゴリズムを天下り的というか、こうなんだよと言い切った上でMATLABによる実装を行いました。
ここではおまけとして、興味ある方がルンゲ・クッタ法を深堀りできるように導く内容を書きます。
図による直感的理解
オイラー法にしろ、ルンゲ・クッタ法にしろ、直感的に何をやってるのか納得できないということはありませんか?
そのような方はぜひ、以下のHPをご覧ください。
ここでは近似式の意味を図で説明してくれています。やはり直感的理解には、視覚に訴える図が一番です。
数式とにらめっこして、どうしても分からない時は図に置き換えてみると、すんなり理解できる事がありますよ。
ルンゲ・クッタ法の近似式の導出
ルンゲ・クッタ法の一番の謎は、やはり近似式ですよね。あれは一体どこから出てきたのか。
その答えは「テイラー展開」です。多変数関数のテイラー展開を考えることで、結果的にあの近似式を導くことができます。
また、冒頭で4次のルンゲ・クッタ法と書きましたが、4次という理由がこのテイラー展開にあって、4回微分の項まで考慮するから4次のルンゲ・クッタ法と言われているのです。
参考になりそうなHPを以下にまとめ、ご紹介します。
まとめ
今回はオイラー法の改良版であるルンゲ・クッタ法を実装しました。
ルンゲ・クッタ法は非常に有名で、仮に自分で実装しなくても知識として知っておいて損はありません。
終わりに
常微分方程式を手計算で解く方法の一つに「解をテイラー級数だとみなす」という方法があります。
実は、あらゆる一変数関数はテイラー級数で表せることが知られています。解は関数ですから、テイラー級数で表せるはずだ、と考えて常微分方程式を解くのです。
ルンゲ・クッタ法をはじめ、数値計算アルゴリズムにテイラー展開が関係するのは、ある意味必然だったのかもしれません。
よろしければ次回の記事も読んでくださると大変嬉しいです。
※本記事に対する改善点や修正点、またはこんな事が知りたいといったご意見がありましたらぜひご連絡ください。
参考HP
[1] らい・ぶらり, 数値計算を使って常微分方程式を解く~ルンゲクッタ法の解説~, 2020/01/19公開, 2020/03/06更新, 2022/10/7閲覧
[2] MONOist, オイラー法とルンゲ・クッタ法を使って微分方程式を解こう, 2015/1/28公開, 2022/10/4閲覧