12回目のMATLAB記事です。
前回申し上げた通り、11回目の続きとなります。
後半となる本記事で扱うのは「二階微分方程式」です。
ファン・デル・ポール方程式
題材とするのは「Van der Pol(ファン・デル・ポール)方程式」という有名な微分方程式です。
以下にそれを示します。
\begin{equation}
\frac{d^2 x}{dt^2} - \mu (1-x^2)\frac{dx}{dt} + x = 0\ (\mu \in \mathbb{R})
\end{equation}
ファン・デル・ポール方程式は、時間 $t$ の関数 $x=x(t)$ についての「二階非線形微分方程式」です。
したがって求める解は $x(t)$ となります。
ファン・デル・ポール方程式は電気回路やバネに関する物理現象を表現できるのですが、その詳細は割愛します。
なお、物理学の世界では時間 $t$ の微分を表す記号としてドット記号を使うことが許されています。
すなわち
\dot{x} \equiv \frac{dx}{dt}
と表現することができます。
これを使ってファン・デル・ポール方程式を書き換えると
\begin{equation}
\ddot{x} - \mu (1-x^2)\dot{x} + x = 0
\end{equation}
となります。
ファン・デル・ポール方程式の実装
方程式の書き換え
さて、ファン・デル・ポール方程式をMATLABで実装します。
ここで、二階(あるいは二階以上)の微分方程式の実装には工夫が必要で、連立一階微分方程式に書き換える必要があります。
その方法は以下の通りです。
二階微分方程式を連立一階微分方程式へ書き換える方法
- $y_1 = x,\ y_2 = \dot{x}$ とおく
- $\dot{y_1},\ \dot{y_2}$を求める
あれこれ説明する前に、まずはこれをファン・デル・ポール方程式に適用してみましょう。
$y_1 = x,\ y_2 = \dot{x}$ とおくと、$\dot{y_1},\ \dot{y_2}$ はぞれぞれ両辺を時間 $t$ で微分することで
\dot{y_1} = \dot{x}=y_2,\ \dot{y_2} = \ddot{x}=\mu (1-{y_1}^2)y_2 - y_1
と求めることができます。
後は両者を連立すれば
\begin{equation}
\left\{ \,
\begin{aligned}
& \dot{y_1} = y_2\\
& \dot{y_2} = \mu (1-{y_1}^2)y_2 - y_1
\end{aligned}
\right.
\end{equation}
となります。
書き換えはこれで終わりです。
続いて、これが何をやっているのか説明しましょう。
繰り返しですが、ファン・デル・ポール方程式は、時間 $t$ の関数 $x=x(t)$ について二階の非線形微分方程式です。
これに対し
y_1 = x,\ y_2 = \dot{x}
なる「変数変換」を考えました。
$y_1$ は $x(t)$ そのものであり、また $y_2$ は $x(t)$ の一次導関数 $\dot{x(t)}$ です1。
本来、$x(t)$ と $\dot{x(t)}$ は微分積分の関係にあるので密接に関係しています。
しかし、そこを敢えて $x(t)$ と $\dot{x(t)}$ が全く別の変数どうしだと考えるのです2。
このような考えに基づき、$x(t)$ に関する一本の微分方程式
\begin{equation}
\ddot{x} - \mu (1-x^2)\dot{x} + x = 0
\end{equation}
を、先ほどの変数変換によって相異なる二つの変数 $y_1,\ y_2$ が混在した二つの微分方程式
\begin{equation}
\left\{ \,
\begin{aligned}
& \dot{y_1} = y_2\\
& \dot{y_2} = \mu (1-{y_1}^2)y_2 - y_1
\end{aligned}
\right.
\end{equation}
に書き換えたのです。
このように、相異なる変数が混在している一階微分方程式を連立したものを、微分方程式の世界で連立一階微分方程式といいます。
これで書き換えの説明は以上です。
プログラムでの実装
さて、本題のMATLABでの実装にうつります。
書き換えた後のファン・デル・ポール方程式を、関数によって次のように実装します。
function Ydot = func(t, Y)
Ydot = zeros(2,1);
mu = 2;
Ydot(1,1) = Y(2);
Ydot(2,1) = mu*(1-Y(1)^2)*Y(2) - Y(1);
end
これは引数 t, Y を受け取って戻り値 Ydot を返す関数です。
まず、戻り値 Ydot を zeros() を使い2行1列の配列として初期化します。
Ydot の第一要素(上側)が $\dot{y_1}$、第二要素(下側)が $\dot{y_2}$ です。
つまり Ydot とは $[\dot{y_1},\dot{y_2}]^T$ を表しています。
引数 Y は $[y_1,\ y_2]^T$ を表しています。
後は変換後の方程式を見ながら間違いなく実装するだけです。
引数 t は時間 $t$ のことです。
関数の中では一度も使ってないのにこれが必要なのかと思うかもしれませんが、必ず要ります。
もし書かない場合はエラーが出るので、試しにやってみてください。
ファン・デル・ポール方程式を解く
それでは解いてみましょう。
t = 0:0.1:20; % 積分範囲
X0 = [1;0]; % 初期値 [x(0); dx(0)/dt]
[t, Y] = ode45(@func, t, X0); % 微分方程式を解く
% グラフの描画
plot(t, Y(:,1), 'b-', 'LineWidth', 1.3) % y1の描画
hold on
plot(t, Y(:,2), 'r-', 'LineWidth', 1.3) % y2の描画
title('Van der Pol')
legend('y1', 'y2')
xlabel('t')
ylabel('y1, y2')
grid on
set(gca, 'FontSize', 14)
function Ydot = func(t, Y)
Ydot = zeros(2,1);
mu = 2;
Ydot(1,1) = Y(2);
Ydot(2,1) = mu*(1-Y(1)^2)*Y(2) - Y(1);
end
解く微分方程式が変わっただけで、前回からの大きな変更点はありません(強いて言えばグラフをちゃんと整えました)。
以下、補足です。
二行目は初期値を設定していますが値が二つありますね。
これは左から $x(0)$ と $\dot{x}(0)$ のことです。
前回は一階微分方程式だったため、初期値として $y(0)$(前回は $x(t)$ を $y(t)$ としていたので $y(0)$)のみを準備すれば良かったのですが、今回は二階です。
二階を解く場合は $x(0)$ だけでなく $\dot{x}(0)$ も必要なのです3。
また、ode45() の戻り値を受け取る配列 Y ですが、ここに $y_1,\ y_2$ が格納されます。
2列の縦長な配列になっていて、1列目が $y_1$ で2列目が $y_2$ です。
補足は以上です。
先ほどのプログラムの実行結果のグラフは次の通りです。
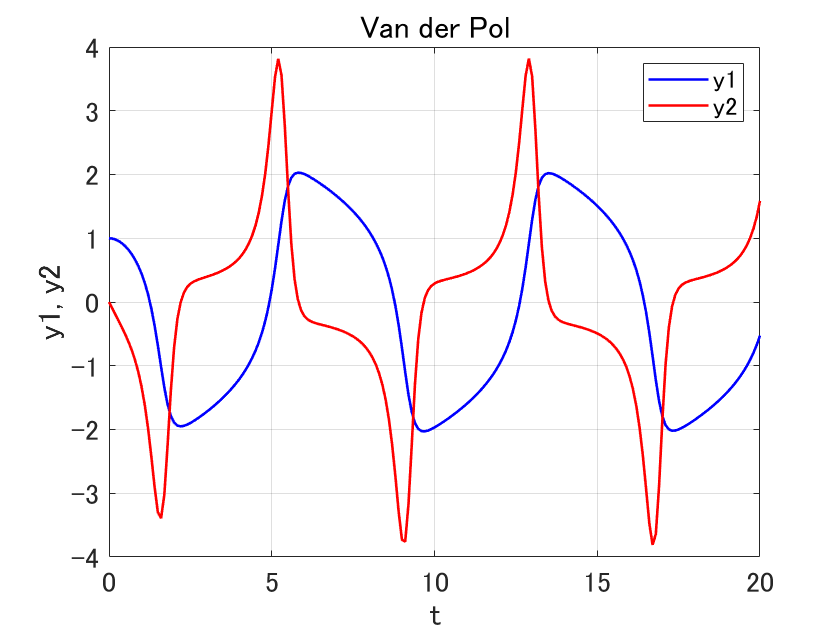
$y_1,\ y_2$ を同時に描画しています。
元々、知りたかったのは $x(t)$ ですので、これだけ知りたければ $y_1$ のグラフのみを見ましょう。
高階微分方程式を解くには
世の中には二階よりもっと大きな階数を持つ微分方程式が存在し、これを高階微分方程式といいます。
これをMATLABで解くにはどうすればいいのか。
勘のいい人は気づいたかもしれませんが、実は二階の時と同じ方法で解けます。
変数の個数は多くなりますが、さっきと同じ方法で連立微分方程式に変換すれば後は簡単です。
$n$ 階微分方程式を連立一階微分方程式へ書き換える方法
- $y_1 = x,\ y_2 = \dot{x},\ \dots,\ y_n=x^{(n-1)}$ とおく
- $\dot{y_1},\ \dot{y_2},\ \dots,\ \dot{y_n}$ を求める
例えば、三階微分方程式であれば $y_1=x,\ y_2=\dot{x},\ y_3=\ddot{x}$ として元の微分方程式を書き換えればOKです。
まとめ
今回は前回からの続きで、二階微分方程式を解きました。
本当に時代の最先端をいく研究ならともかく、大学および大学院での講義や研究レベルであれば問題なく、微分方程式をMATLABで解くことができると思います。
解けないものがあるとすれば、よほど特殊なものか、もしくは「偏微分方程式」でしょう。
終わりに
連立微分方程式への書き換えについて、あれは制御理論を専攻している人にとってはかなり馴染み深いものです。
現代制御論という枠組みの中に状態空間表現というものがあって、これは今回と全く同じ方法で微分方程式を書き換えたものです。
つまり今回実装した連立微分方程式が、まさに状態空間表現なのです。
という制御理論専攻からの豆知識でした。
よろしければ次回の記事も読んでくださると大変嬉しいです。
※本記事に対する改善点や修正点、またはこんな事が知りたいといったご意見がありましたらぜひご連絡ください。