4回目のMATLAB記事です。
今回の内容は3回目の続きにあたります。
前回、最低限の2次元グラフの描き方を説明しました。最低限といっても、あの内容
身に付ければ人に見せられるグラフを十分に作成可能です。
今回は痒い所に手が届くような図の作成技術を4つご紹介します。
複数のグラフを1枚の図に重ねて描画する
前回の記事では $y=\text{sin}x\ (0 \leq x \leq 2\pi)$ の図を作成しました。
そのプログラムと作成した図を以下に示します。
x = 0:pi/100:2*pi;
y = sin(x);
plot(x,y, 'LineWidth', 2)
title('y = sinx')
xlabel('x')
ylabel('y')
legend('sin')
xlim([0, 2*pi])
ylim([-1.5, 1.5])
grid
set(gca, 'FontSize', 13)
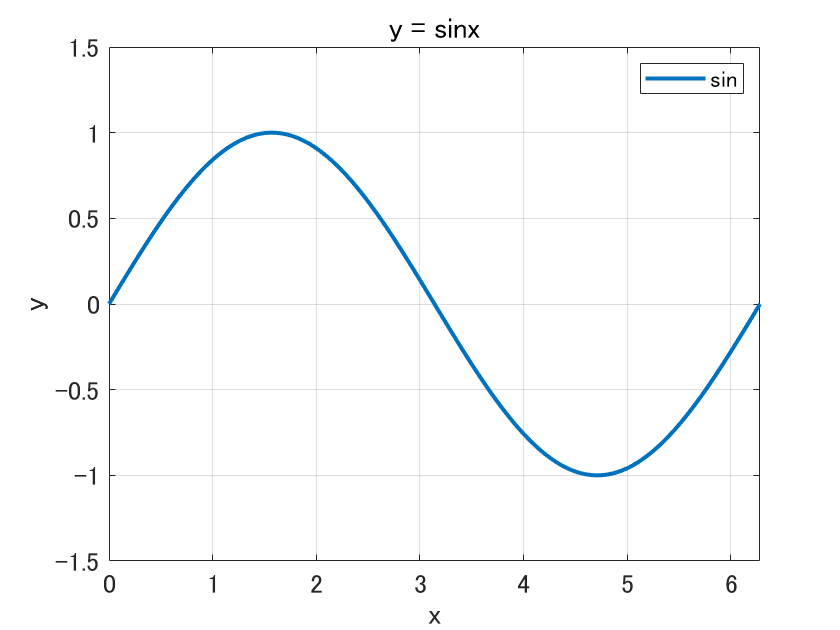
ここへさらに $y=\text{cos}x\ (0 \leq x \leq 2\pi)$ のグラフを重ねて描画してみましょう。
x = 0:pi/100:2*pi;
y1 = sin(x); %変更
y2 = cos(x); %追加
plot(x,y1, 'LineWidth', 2)
hold on %追加
plot(x,y2, 'LineWidth', 2) %追加
title('sinx, cosx') %変更
xlabel('x')
ylabel('y')
legend('sin','cos') %変更
xlim([0, 2*pi])
ylim([-1.5, 1.5])
grid
set(gca, 'FontSize', 13)
前回の記事を見ていただけた人ならば、なんとなく意味が分かるのではと期待します。
1行目の x を用意して x の各値に対する $\text{sin}x$ と $\text{cos}x$ をそれぞれ y1 と y2 に格納します。
ここで新しく「hold on」というものが出てきました。これは描画したグラフをそのまま残してくださいという指示になります。もしこれを書かない場合 $\text{sin}x$ と $\text{cos}x$ が重ねて描画されません。
このように、複数個のグラフを1枚の図に重ねたい時は hold on を使いましょう。
後は大きな変更点はありません(強いて言えば legend() と title() の中身を変えましたが)。
それでは実行してみましょう。
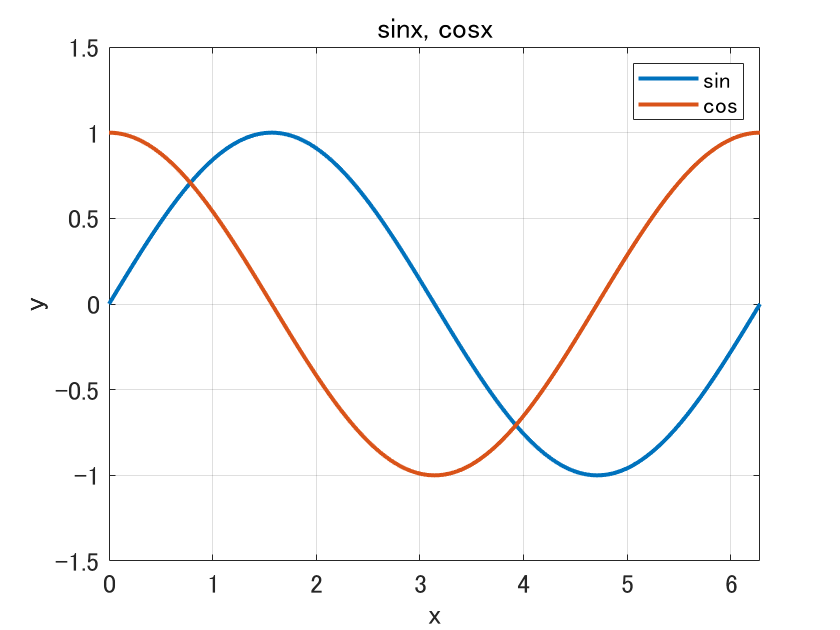
ちゃんと重ねて描画されましたね。
グラフの線の種類を変える
2つのグラフは実線で描かれています。しかし点線など、実線以外でグラフを描きたい場合もあるでしょう。
その時は plot() 内で指定しましょう。
x = 0:pi/100:2*pi;
y1 = sin(x);
y2 = cos(x);
plot(x,y1, ':', 'LineWidth', 2) %点線に変更
hold on
plot(x,y2, '-.', 'LineWidth', 2) %一点鎖線に変更
title('sinx, cosx')
xlabel('x')
ylabel('y')
legend('sin','cos')
xlim([0, 2*pi])
ylim([-1.5, 1.5])
grid
set(gca, 'FontSize', 13)
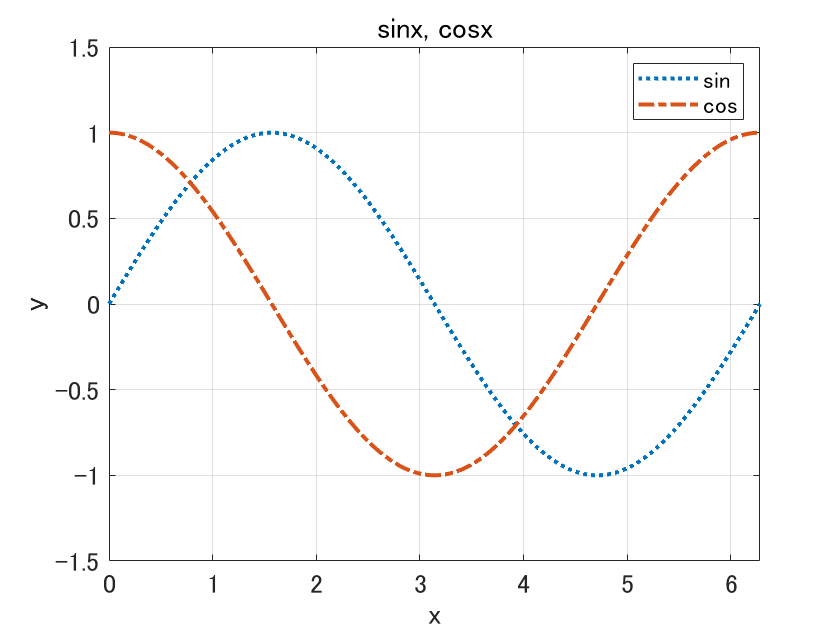
「:」は点線に、「-.」は一点鎖線にしてくださいという意味になります。ちゃんと実線から変更されていますね。
線の種類については以下の参考にしてください。
グラフの線の色を変える
自分の都合に合わせてグラフを色分けしたい時があります。
その時も plot() 内で指定しましょう。
x = 0:pi/100:2*pi;
y1 = sin(x);
y2 = cos(x);
plot(x,y1, 'r:', 'LineWidth', 2) %赤色の点線に変更
hold on
plot(x,y2, 'b-.', 'LineWidth', 2) %青色の一点鎖線に変更
title('sinx, cosx')
xlabel('x')
ylabel('y')
legend('sin','cos')
xlim([0, 2*pi])
ylim([-1.5, 1.5])
grid
set(gca, 'FontSize', 13)

線の種類を変えた部分と同じ個所に変更を加えます。
rは赤(red)、bは青(blue)を表しています。これ以外にも色がある上、RGB値による指定や16進数カラーコードも使用できます。
ここでは色を変更できることを説明するために、何も考えず色を選びました。
実際にプレゼンなどで見てもらう時は、きちんと色合いを考えた方がいいです。見やすさや見栄えは大切です。
なお、色の変更と線の種類の変更は同時に行えます。例えば「r:」は赤色の点線という意味になります。色だけを変えて実線のままでいい時は色だけを指定してください。
色の指定に関する詳細は以下を参考にしてください。
変数の中身を凡例にする
num2str()を使えばこれが可能です。これは変数の型をint型、double型からString型に変えるコマンドです。
x = 0:pi/100:2*pi;
y1 = sin(x);
y2 = cos(x);
a=1; %追加
b=2; %追加
plot(x,y1, 'r:', 'LineWidth', 2,...
'DisplayName',[num2str(a),'つめのグラフ:sin']) %変更
hold on
plot(x,y2, 'b-.', 'LineWidth', 2,...
'DisplayName',[num2str(b),'つめのグラフ:cos']) %変更
title('sinx, cosx')
xlabel('x')
ylabel('y')
legend %変更
xlim([0, 2*pi])
ylim([-1.5, 1.5])
grid
set(gca, 'FontSize', 13)

ここでは legend() の中ではなく、敢えて DisplayName で凡例を書きました。
[]で囲むと文字を連結して一つの長い凡例を作り出すことができます。長すぎる凡例は好まれませんけどね。
MATLABでは「...」を文の末尾に書いた場合、その部分と改行した直下の部分とがプログラムとしてつながっていると判断します。
私の経験上、num2str() と DisplayName を使った凡例の書き方は知っておくと便利です。
例えば、4個以上をグラフを重ねて描画する時にfor文を組み合わせると思いますが、その時にループ用の変数(例えば i や j)を凡例にするんです。簡単なプログラム例を示すと
for i = 1:4
plot(x(i,:), y(i,:), 'r:', 'LineWidth', 2,...
'DisplayName',[num2str(i),'つめのグラフ'])
end
という書き方ができます。つまりfor文の中「1つめのグラフ」、「2つめのグラフ」...という凡例を作ってくれるわけです。
これについてはfor文の記事を出すので、その中で詳しく説明したいと思います。
凡例の位置を変える
凡例の位置は自由に変えることができます。
一番手っ取り早いのは凡例をドラッグ&ドロップすることです。
プログラムを実行して図を表示させ、その凡例をドラッグ&ドロップしてみてください。図の枠内であれば自由に動かせると思います。
また legend() を以下のように変更して、凡例の位置を指定することもできます。
x = 0:pi/100:2*pi;
y1 = sin(x);
y2 = cos(x);
plot(x,y1, 'r:', 'LineWidth', 2)
hold on
plot(x,y2, 'b-.', 'LineWidth', 2)
title('sinx, cosx')
xlabel('x')
ylabel('y')
legend('sin','cos','Location','south')
xlim([0, 2*pi])
ylim([-1.5, 1.5])
grid
set(gca, 'FontSize', 13)
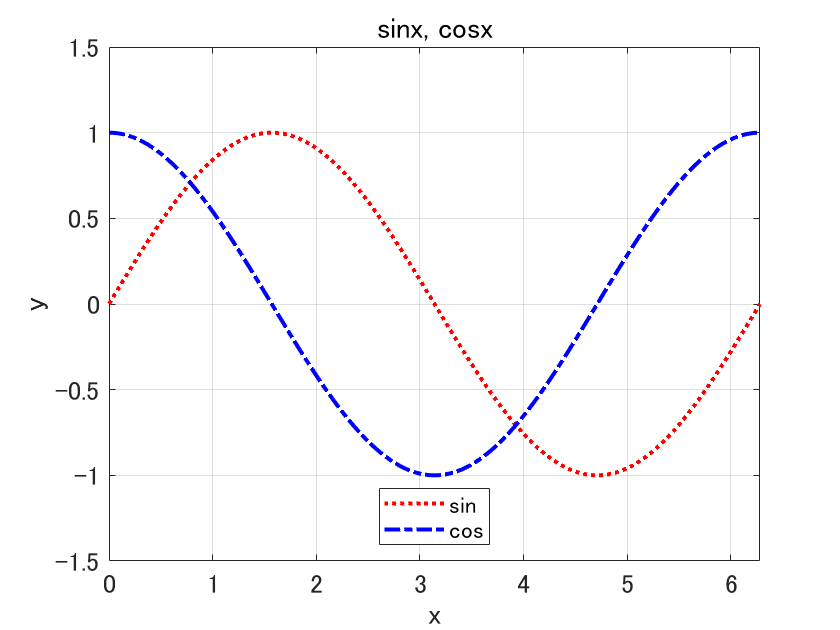
Location というプロパティがあって、その値を south にしました。凡例が図の南側に表示されましたね。
詳しくは以下を参考にしてください。
まとめ
今回は3回目の補完として以下の内容を説明しました。
- 複数のグラフを1枚の図に重ねて描画する
- グラフの線の色を変える
- 変数の中身を凡例にする
- 凡例の位置を変える
これだけ身に付ければ、2次元グラフの図の作成で不自由を感じることはほぼないと思います。
終わりに
前回、生物である人間は数字や数式よりも五感を扱う方が得意だというお話をしました。それで一つ思い出したことがあります。
Youtubeで数か月前に、面白い内容の動画を見つけたのでその概要を紹介します。(本来はその動画のURLを記載したいのですが、見つからなくて...。本当にすみません。)
それは、ある男性が観衆に向けて講演(もしくは講義)を行っている動画でした。
$x=3$ (ただし数式はうろ覚えです)
という等式があったとします。"$x$"という記号と"3"という記号がイコール、すなわち同じであると主張しています。
世の中にはこの等式に疑問を持ち、また理解できない方がいるそうなのです。$x$ と3が同じなんてありえない、おかしいと。
念のために書きますが、この文章に馬鹿にする意図は一切ありません。また、勉強したくてもできない方がいる、のような社会問題を言及しているわけでもありません。
では、なぜ疑問を持つのでしょうか。その理由は簡単で見た目が全然違うからです。
$x$ と3はどちらも記号であり、見た目が全然違います。だから両者が同じだという主張に疑問を持つわけです。
しかし両者を「=」で結ぶと、一般的には両者が同じだと通じると思います。
実は、人類が開発したこの「=(イコール)」という記号はかなり特別だというお話でした。
初めてこの動画を見た時に思わず、はぁ~なるほどな~、と呟いてしまいました。私にとっては色々と思考を巡らす価値のある内容でしたね。
※本記事に対する改善点や修正点、またはこんな事が知りたいといったご意見がありましたらぜひご連絡ください。