9回目のMATLAB記事です。
今回から専門的な内容をやっていこうと思います。
私は「制御理論」と「機械学習」を専攻していまして、MATLABもそのためのツールとして利用しています。特に前者はMATLABの真価を発揮できる分野の一つです。
そのこともあって、私の記事では両者に焦点を当て、主に初心者向けの記事を作って(内容を展開して)いきたいと考えています。
MATLABでは、この二つ以外にも信号処理や数値計算といった様々な事が行えます。しかし私はそれらの分野に関して全くの専門外ですので、悪しからず...。
さて、今回の主役は「固有値分解」です。
固有値分解は制御理論では必ず登場します。また機械学習(や統計学)では主成分分析で活躍しています。
本記事はある程度の線形代数の知識を前提にしています。
固有値と固有ベクトル
ある $n$ 次元の正方行列 $A$ に対して
A\boldsymbol{p}=\lambda \boldsymbol{p}\ (\boldsymbol{p} \in \mathbb{C}^n,\ \boldsymbol{p} \neq \boldsymbol{0},\ \lambda \in \mathbb{C})
を満たすスカラ $\lambda$ を固有値といい、$\boldsymbol{p}$ のことを固有ベクトルといいます。
$A$ が $n$ 次元ですので、その固有値 $\lambda$ は重複を含めて $n$ 個あります。しかし、ここでは簡単のため $n$ 個全てが異なる値だとします。
また、それに伴って固有ベクトル $\boldsymbol{p}$ も $n$ 個あります。
つまり、固有値が $\lambda_{1},\ \lambda_{2},\ \dots,\ \lambda_{n}$ とすれば、それぞれに対応する固有ベクトルが $\boldsymbol{p}_1,\ \boldsymbol{p}_2,\ \dots,\ \boldsymbol{p}_n$ となるわけです。
固有値と固有ベクトルの直感的意味
固有値と固有ベクトルの求め方は、今や分かりやすい線形代数の書籍やインターネットページがたくさんあります1。
また、私は記事のメインとなる部分をMATLABのプログラミングにしたいと考えています。
そこで、ここでは固有値と固有ベクトルの求め方を割愛して、両者とあの式の直感的な意味を与えたいと思います。
例として、以下の二次元正方行列の固有値と固有ベクトルを考えます。
\begin{equation}
A=
\begin{pmatrix}
8 & 1\\
4 & 5
\end{pmatrix}
\end{equation}
固有値は二つあって、$\lambda_1=4,\ \lambda_2 = 9$ です。また、各固有値に対する固有ベクトルは $\boldsymbol{p}_1=(-1,4)^T,\ \boldsymbol{p}_2=(1,1)^T$ です。
固有ベクトルを図示すると以下のようになります。スケールは全く関係ありません。
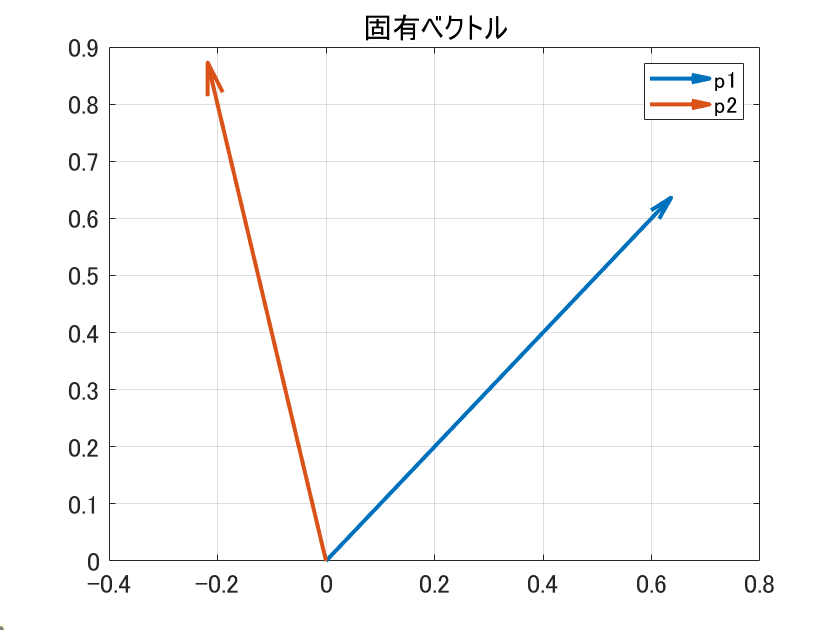
この二つの固有ベクトルに行列 $A$ をかけると、それは固有ベクトルにそれぞれ対応する固有値をかけたものと同じである、というのがあの式を図形的に考えた際の意味となります。
つまり、行列 $A$ を固有ベクトル $\boldsymbol{p}$ に掛けると、その固有ベクトルは $\lambda$ 倍されるということです。
実際に計算してみると
\begin{equation}
A\boldsymbol{p}_1=
\begin{pmatrix}
8 & 1\\
4 & 5
\end{pmatrix}
\begin{pmatrix}
-1\\
4
\end{pmatrix}
=
\begin{pmatrix}
-4\\
16
\end{pmatrix}
\end{equation}
\begin{equation}
A\boldsymbol{p}_2=
\begin{pmatrix}
8 & 1\\
4 & 5
\end{pmatrix}
\begin{pmatrix}
1\\
1
\end{pmatrix}
=
\begin{pmatrix}
9\\
9
\end{pmatrix}
\end{equation}
となり、確かに固有ベクトルが固有値倍されていることが分かります2。
数式が出てきて「うえー...」と思うかもしれませんが、主張したいことはこんなに単純なのです。
さらに、固有値と固有ベクトルは行列ごとに異なっていて、両者はその行列の特徴を反映した存在だといえます。
固有値分解
求めた固有ベクトルを
\begin{equation}
P=
\begin{pmatrix}
\boldsymbol{p}_1 & \boldsymbol{p}_2 & \dots & \boldsymbol{p}_n
\end{pmatrix}
\end{equation}
のように一つの行列 $P$ としてまとめあげます。$P$ とその逆行列 $P^{-1}$ を用いると行列 $A$ を
\begin{equation}
P^{-1}AP=\begin{pmatrix}
\lambda_1 & 0 & \dots & 0\\
0 & \lambda_2 & \dots & 0\\
\vdots & \vdots & \ddots & \vdots\\
0 & 0 & \dots & \lambda_n
\end{pmatrix}
\end{equation}
のように、$A$ の固有値が対角に並び、それ以外の要素が全て$0$ の対角行列を作ることができます。
こうすることで、行列 $A$ の特徴を表す固有値を全て抜き出しているのです。
これを行列 $A$ の対角化といいます。
さらに、$P^{-1}$を両辺右側から、$P$を左側からかけることで
\begin{equation}
A=P\begin{pmatrix}
\lambda_1 & 0 & \dots & 0\\
0 & \lambda_2 & \dots & 0\\
\vdots & \vdots & \ddots & \vdots\\
0 & 0 & \dots & \lambda_n
\end{pmatrix}P^{-1}
\end{equation}
とできます。これを行列 $A$ の固有値分解といいます。
固有値分解の実装
MATLABでの固有値分解の実装はものすごく簡単です。
A=[8, 1; 4, 5];
[P, lambda] = eig(A); %固有値と固有ベクトルを求める
lambda % 対角化した行列
P % 固有ベクトルをまとめた行列
P*lambda*P^(-1) % 固有値分解
lambda =
9 0
0 4
P =
0.7071 -0.2425
0.7071 0.9701
ans =
8 1
4 5
2行目のeig() コマンドが、固有値と固有ベクトルを求めるコマンドです。
変数 P が固有ベクトルを横に並べ、まとめあげた配列です。lambda が固有値を対角化した状態で格納した配列です。
固有値と固有ベクトルは対応した形になっています。
例えば、lambda(1,1) は固有値 $9$ で、その固有ベクトルが P の一列目になっています。同様に、lambda(2,2) は固有値 $4$ で、その固有ベクトルが P の二列目になっています
P に格納された固有ベクトルは、先に示したものと随分見た目が違いますが、心配ありません。ちゃんと元の固有ベクトル(のスカラ倍)と同じものです。
5行目は固有値分解を実装しています。変数 ans に元の行列 $A$ が格納されています。
固有ベクトルの図示の実装
先ほどの固有ベクトルの図示は、以下のようなプログラムで描画できます。
ただし、固有値が全て異なる二次正方行列でないと使用できません。
A=[8, 1; 4, 5];
[P, lambda]=eig(A);
p1 = P(:,1); %p1
p2 = P(:,2); %p2
quiver(0,0,p1(1),p1(2),'LineWidth',2) %p1の描画
hold on
quiver(0,0,p1(1),p2(2),'LineWidth',2) %p2の描画
title('固有ベクトル')
legend('p1','p2')
set(gca,'FontSize',13)
grid on
MATLABで二次元ユークリッド空間に矢印やベクトルを描画するには quiver() コマンドを使います。
第一引数と第二引数に、それぞれベクトルの始点のx座標、y座標を指定します。今回は原点を指定したので0としています。
第三引数と第四引数に、ベクトルの向き(傾き)を表すx座標、y座標を指定します。例えば $y=2x$ と同じ向きになってほしければ1、2を指定すればOKです。
今回は矢印の向きが固有ベクトルに一致してほしいので、x座標=p1(1), y座標=p1(2)と指定しました。
まとめ
今回は固有値分解を説明しました。
固有値分解は、線形代数の一つのゴールであるジョルダン標準形の入門編のような存在です。
入門編でありながら非常に実用的で、色んな学問で応用されています。冒頭でも述べた通り、私の専攻である制御理論と機械学習でも活躍しています。
そのため、個人的に線形代数で一番印象に残っている部分です。
終わりに
人間は個性という名の固有値の集合体だと、私は考えています。
名前、性格、特技、好み、得手不得手など無数の固有値がその個人を作り上げているのです。
名前といえば、近年、キラキラネームが色々と議論されていますね。
名前はその人の個性の一つであり、品詞でいえば固有名詞です。固有名詞は名付けられたその事物を特定する働きを持っています。例えば「富士山」と聞いたら、思い浮かべるのはあの山だけですよね?
ただ、人間の名前とは特別で不思議なものです。
その人にとって名前は生涯使い続けるものですし、なにより親からの最初の贈り物です。また「名は体を表す」という言葉があるように、名前に込められた意味の通りにその人が育っていく、という主張もあるくらいです。
名前には、単なる固有名詞としての役割だけでなく、科学では説明の付かないパワーを秘めているような気がします。
で、キラキラネームが名付けられた個人にとって、それらの役目を果たせればいいのですが、基本的に私はそう思えないです。
また、繰り返しですが人間は個性(固有値)の集合体。名前はその一つであり、それだけが個人を作り上げるわけではありません。
例えば、元プロ野球選手の鈴木一朗氏なんて、書類の記入例に出てきそうなほど一般的な名前です。にもかかわらず「鈴木一朗」という名前を聞けば、誰もがあの人を思い浮かべることでしょう。
子どもには、その生き様を良い意味で支えるような名前を付けてあげたいものです。
よろしければ次回の記事も読んでくださると大変嬉しいです。
※本記事に対する改善点や修正点、またはこんな事が知りたいといったご意見がありましたらぜひご連絡ください。
参考HP
[1] HEADBOOST, プログラマーのための線形代数 | 行列の分解 | 固有値分解, 運営責任者:MORIYAMA, 2021年11月27日更新, 2022/08/02閲覧.
[2] 同志社大学, オープンコースウェア, 線形代数 13 固有値, 浦部治一郎, 2022/08/02閲覧.