5回目のMATLAB記事です。
今回は「3次元グラフの描き方」を説明します。2次元グラフの描き方をマスターした方なら、難なく理解できるでしょう。
また、今回は行列の演算に関して初心者の引っかかりやすいところが登場します。
曲線の描画
まずは、3次元空間に曲線を描いてみましょう。
それには plot() の3次元版といえる plot3() を使います。
t = 0:pi/100:6*pi; %媒介変数
x = cos(t);
y = sin(t);
z = t;
plot3(x,y,z,'LineWidth',2)
title('らせん')
xlabel('x')
ylabel('y')
zlabel('z') %z軸の名前
grid on
set(gca, 'FontSize',13)

手っ取り早く螺旋を描いてみました。
2次元グラフの描き方と非常に似ているため、プログラムについて多くを語る必要はないでしょう。
plot3() にx、y、z座標の値(の配列)を渡せば曲線を描画してくれます。
曲面の描画
次は3次元空間に曲面を描いてみましょう。題材とする数式は以下の通りです。
\begin{equation}
z = \frac{x^4}{32} + \frac{y^4}{28} - x^2 - y^2 + x + y + 30
\end{equation}
描く方法として surface() や meshc() など複数の方法があります。
surface()
まずは surface() を使ってみます。
[x, y] = meshgrid(-6:0.25:5.5);
z = (x.^4)/32 + (y.^4)/28 - x.^2 - y.^2 + x + y + 30;
surface(x, y, z)
xlabel('x')
ylabel('y')
zlabel('z')
title('surface()を使った曲面の描画')
set(gca, 'FontSize', 13)
view(3) %カメラの目線を設定
grid on
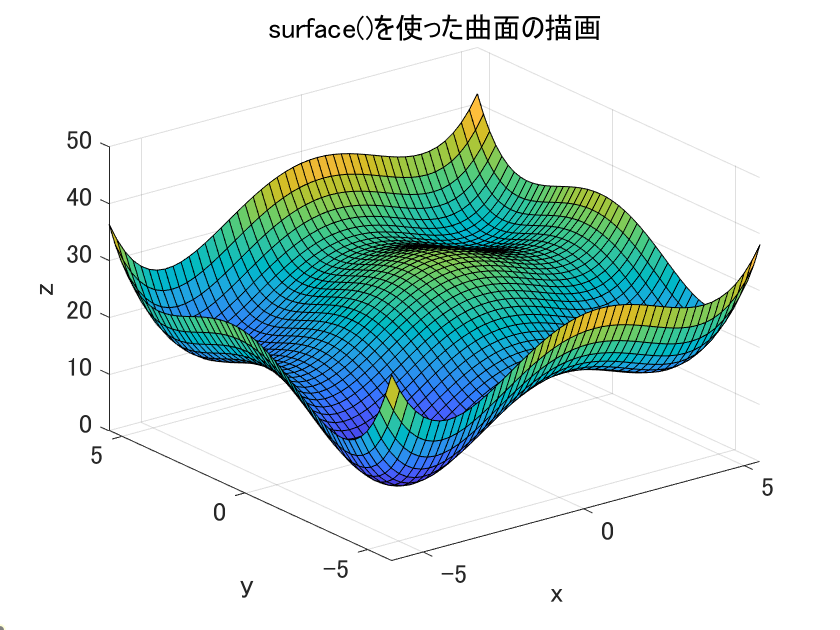
曲面の概形についてはこんなものだと思ってください。ここではプログラムの説明をします。
まず1行目ですが、これは
\begin{equation}
D = \{(x,y) | -6 \leq x \leq 5.5,\ -6\leq y \leq 5.5\}
\end{equation}
なる領域 $D$ の全ての $(x,y)$ を用意してくださいという意味です。
(※ただし $x,y$ の範囲を0.25刻みにしてるので厳密な表現ではありません。)
ピンとこない方のために以下の図を用意しました。

これは描画した曲面を真上から見た図です。曲面は上から見ると2次元グラフになりますね。
格子みたいになってますが、交差したところと境界線上の座標を用意してくださいということです。
なお、この図は先ほどのプログラムでview(3)のところをview(2)にするだけで描画できます。
これはグラフを眺めるカメラの目線を設定するコマンドです。
view(3)の場合、3次元グラフとして眺めるということになります。view(2)の場合、2次元グラフとして眺めることになります。
view()については以下を参考にしてください。
次に2行目です。用意した $(x,y)$ に対する $z$ の値を求めます。
ここで気になる所がありますよね? 行列の累乗のところに「.(ピリオド)」が付いています。
実はこれがMATLAB初心者が引っかかりやすいところです!
累乗にしろ積にしろ、ベクトルや行列の演算子の前に「.」を付けると要素ごとに演算してくださいという意味になります。
百聞は一見に如かず。適当なベクトルや行列を用意してその違いを見てみましょう。今回は
\begin{equation}
A=\begin{bmatrix}
1 & 2 & 3\\
4 & 5 & 6\\
7 & 8 & 9
\end{bmatrix}
\end{equation}
という3次正方行列 $A$ を用意します。
まずは「.」を付けなかった場合です。
>> A = [1 2 3; 4 5 6; 7 8 9];
>> A^4
ans =
7560 9288 11016
17118 21033 24948
26676 32778 38880
単純に行列 $A$ を4回かけた結果となります。
続いて付けた場合です。
>> A.^4
ans =
1 16 81
256 625 1296
2401 4096 6561
結果が各要素の4乗になってますね。
このように「.」を付けて要素ごとに4乗してもらわないと $z$ の値を正しく求められません。ここで初心者が引っかかり「.」をつけ忘れてしまうんですよね。
長くなりましたがプログラムの説明は以上です。
surface() については以下の参考にしてください。
meshc()
続いて meshc() を使ってみます。
[x, y] = meshgrid(-6:0.25:5.5);
z = (x.^4)/20 + (y.^4)/28 - x.^2 - y.^2 + x + y + 30;
meshc(x, y, z)
xlabel('x')
ylabel('y')
zlabel('z')
set(gca, 'FontSize', 13)

ほぼ、先ほどのプログラムと変わりません。
なんとなくこっちの方が明るくて見やすいですね。私だけかもしれませんが。
meshc() については以下の参考にしてください。
等高線の描画
義務教育の時に社会科で習ったと思いますが、ある山の同じ高さの部分を線で結んだものを等高線といいます。
ここでは先ほどの数式に対する等高線を描画したいと思います。
それには contour() を使います。
[x, y] = meshgrid(-6:0.25:5.5);
z = (x.^4)/20 + (y.^4)/28 - x.^2 - y.^2 + x + y + 30;
figure
meshc(x, y, z)
xlabel('x')
ylabel('y')
zlabel('z')
title('meshc()を用いた曲面の描画')
set(gca, 'FontSize', 13)
figure
contour(x, y, z, 25)
xlabel('x')
ylabel('y')
set(gca, 'FontSize', 13)
title('等高線')

二つのグラフが出てくると思います。一つ目が meshc() の時と同じもの、二つ目が等高線の図です。前者はここでは割愛します。
等高線を書くと2次元平面を見るだけである程度、3次元の曲面の特徴(凹凸具合など)が分かります。
私の知る限り、等高線は主に連続関数の最適化にて活躍します。
contour() については以下を参考にしてください。
まとめ
今回は3次元グラフの描き方を説明しました。使う関数が変わっただけで本質は2次元の時と変わりません。
今回の主なコマンドをまとめます。
- plot3():曲線の描画
- surface(), meshc():曲面の描画
- contour():等高線の描画
また、今回説明した「.(ピリオド)」は引っかかりやすいので要注意です!
終わりに
我々の生活するこの世界は4次元空間です。3次元空間に時間軸を足して3+1=4次元です。
某ネコ型ロボットの秘密道具「時門」が存在すれば、それを使って世界の時を止めることでこの世界を3次元グラフとして眺めることができるわけです。
我々は4次元世界にいるのでそれより大きな次元、つまり5次元以上の世界を観測することができません。
5次元というのは、例えば我々の住む宇宙を「宇宙A」とすると「宇宙B」「宇宙C」...と、我々の知らない宇宙がたくさん存在するということです。
世の中には6次元以上の世界について考える方もいるみたいで、私には色々な意味で想像できない世界です(笑)。
よろしければ次回の記事も読んでくださると大変嬉しいです。
※本記事に対する改善点や修正点、またはこんな事が知りたいといったご意見がありましたらぜひご連絡ください。