概要
初学者向けのPythonの参考書を学習後、AIや機械学習に興味を持ち、オンラインプログラミングスクールの「Aidemy」でデータ分析講座6ヶ月コースを受講しました。
本記事では、講座の成果物として株価予測に挑戦した結果をまとめています。
- 「データ分析に興味があるけど、Aidmeyで本当にスキルを身に着けられるのか不安を感じる、、」
- 「Aidmeyを受講するとどういったことが出来るようになるのか、イメージを知りたい!」
といった方々の一助になれば幸いです。
結論としましては、私自身Aidmeyを受講したことで主に次のことを学ぶことが出来ました。
- Pythonの基本的な使い方
- AI、機械学習の概要
- 一般的に利用される機械学習モデルの種類、利用先
- Pythonを用いたデータの前処理
- Pythonで機械学習を行う方法
- Kaggleの利用方法と進め方(タイタニックの生存者予測モデルを作成)
講座終了後、私も含めて未経験から転職に成功している方も多数いらっしゃるため、初心者が初めに学ぶこととしては十分な内容であると思いました。
ただし、機械学習モデルや分析結果の理解・考察をより詳細に行うためには、自身で補完が必要な場面もありました。
特にKaggleの課題では、学んだことの活用方法を確認することができ、記憶の定着とスキルアップにとても効果的でした。
「なぜこの前処理をするのか」、「与えれたデータのどこを確認すればよいか」といった点について詳細な説明があるため、「なにをどういった手順で」分析しているのかがわかりやすかったです。
わからない点はチャットやオンライン自習室上で講師の方に質問することが出来るため、安心して進めることが出来ます。
それでは株価の変動予測に挑戦した結果を下記に示します。
1. 背景・目的
1.1 背景
株価は日々変動し、予測が困難です。将来の株価の予測には、テクニカル分析のように過去の値動き等から予測する手法や、過去の財務諸表、業績等を基に、企業の本質的な価値に対して現在の株価が割安であるか否かを分析するファンダメンタルズ分析といった手法が用いられます。
データ分析講座の中では、テクニカル分析の一環として過去のニュース記事のネガポジ分析結果と株価データから、将来の株価の変動を予測するモデルを作成しました。
成果物ではS&P500を対象に、データ分析講座で用いた過去のニュース記事の代わりに、アメリカの株式市場に関する情報を発信するTwitterアカウントから取得したツイートを使用しました。
各ツイートをネガポジ分析した結果、及び過去のS&P500のデータを基に機械学習を用いた予測モデルを構築し、将来の株価変動を予測可能であるかを確認しました。
原理的には株価が未来で上昇するのであれば、現時点で購入しておくことで株価が上がった際の上昇分をキャピタルゲインとして得ることが出来ます。
逆に未来において株価が下落するのであれば、現時点で売却することにより、損失を回避することが出来ます。
本来S&P500は長期投資を目的にインデックスファンドの形式で購入され、短期の値動きに一喜一憂する類のものではありません。S&P500の場合、ホールドする期間が長くなるほど損をする確率は減少することが過去の知見からわかっています。
今回作成した予測モデルは、成果物の一環としてあえてS&P500を短期間で売買するケースを想定しています。
1.2 目的
Twitterのネガポジ分析結果、及び株価データを基に構築した株価変動予測モデルを用いてS&P500の価格変動を予測可能であるかを評価する。
2. 予測モデル構築に係る諸条件
- 対象とした株価指数は、アメリカの主要500社に投資するS&P500指数
- 取引が行われている日のツイート、株価のみを使用
- データ(ツイート、株価)の取得期間は2022年10月から2023年1月の4か月間
- 極性辞書には、高村らの単語感情極性対応表(高村ほか, 2006; Takamura et.al, 2005)を使用
- 実行環境にはGoogle Colaboratoryを使用。
3. データの取得
3.1 TwiterAPIの申請方法
Twitterアカウントからツイートを取得するための方法はいくつかあります。
その中でも今回はTweepyというモジュールを使用しました。
Tweepyを使用するためには、事前にTwitterAPIの利用登録が必要となります。
TwitterAPIには執筆時点(2023年2月22日時点)で以下の2種類のバージョンがあり、V2が最新です。
- API V1.1
- API V2
さらに、TwitterAPI V2は以下のアクセスレベルに分かれています。
- Essential
- Elevated
- Academic Research
Essentialは、月に50万ツイートまで取得することが出来、利用登録後にすぐに使用を開始することが出来ます。
Elevatedは申請が必要となりますが、月に200万ツイートまで取得することが可能です。
今回は「TwitterAPI V2 Essential」を利用しました。このAPIグレードでは、1つのアカウントから3200件までしかツイートを取得することが出来ないため、アカウントを選定する際は最低でも4カ月分のツイートを取得できるよう、1日のツイート数が35ツイート前後であることを確認しました。
TwitterAPIの利用については、度々ニュースにもなっている通り使用条件が今後更新される可能性があるため、利用する際は最新の情報をご確認ください。
以下にTwitterAPI利用時に参考としたサイトを示します。
【参考サイト】
- 【2022年度最新版】Twitter API 申請方法(Twitter v1.1 v2対応)
- Twitter API v2 の Essential Access ができた手順メモ
- 【Python】Tweepyを使用して、Twitterからツイート取得、自動投稿(画像付き) – V1.1、V2 両方対応 –
利用登録後、API KEY、API KEY SECRET、ACCESS TOKEN、ACCESS TOKEN SECRET、BEARER TOKENといったコードを取得してください。
これらは再取得することも可能です。
3.2 対象としたTwitterアカウント
予測モデルの構築に用いた各アカウントのリンクとプロフィール欄の記載を示します。どのアカウントもアメリカの株式市場に関するニュースや考察を日々発信しています。
当初はニュースサイトやアメリカの著名な投資家、経営者のツイートも含める計画でしたが、ツイート数が多く、数カ月に渡って取得することが困難であったり、そもそもツイート数が少なすぎるため止めました。
実際にデータを取得して内容を確認すると、計画と照らして情報量が十分でないこともありました。
こういったケースにも柔軟に対応できるよう、工程上のマージンを確保しておくことが必要であることを学びました。
Breaking news, smart analysis and in-depth features on global markets and finance from The Wall Street Journal.
Guiding investors of all experience levels through the stock market using time-tested strategies and actionable insights.
Finance News & Media. Twitter Delayed. Latest News + Active community
Sharper Insight. Smarter Investing.
次にツイートを取得するためのコードを示します。
ツイートは2つのプロセスに分けて取得しました。はじめにコード1を実行し、最初の100件を取得します。次にコード2を実行し、コード1の最後のツイートのツイートidを基に残りのツイートを連続で取得しました。
この「100件取得→残りの期間分を取得」を、対象としたアカウントのすべてに実行しました。
<コード1>
今回のモデルではリツイートは含めていません。
※Google Colaboratoryでモジュールをインストールする場合、pipの前に「!」を付けます。
APIキーには、利用申請時に取得したものを入力します。
.get_user()の引数の説明は次の通りです。
- user.data.id:ユーザーごとに割り当てられる識別idを意味します。「@xxx」といったアカウントidとは別物です。
- max_results:1回の実行で取得するツイート数を意味します。最大100件です。
- exclude:取得する情報のうち、必要のない情報を指定することが出来ます。ここでリツイートは含めない設定をしています。
- tweet_fields:["created_at", ]とすることで、ツイートされた日時を取得することが出来ます。
- untiil_id:ツイートごとに割り振れるidです。2回目の実行では、最初に取得した100件目のidを入力することで、そのidよりも過去のツイートを取得することが出来ます。
- user_auth:TwitterAPIの認証情報に関する引数です。
# tweepyのインストール
!pip install tweepy --upgrade
import csv
import tweepy
API_KEY = ""
API_KEY_SECRET = ""
ACCESS_TOKEN = ""
ACCESS_TOKEN_SECRET = ""
BEARER_TOKEN = ""
client = tweepy.Client(BEARER_TOKEN)
api = tweepy.Client(None, API_KEY, API_KEY_SECRET, ACCESS_TOKEN, ACCESS_TOKEN_SECRET)
person_list = ["WSJMarkets","IBDinvestors","benzinga","Investopedia"]
# 取得するアカウントを指定
person_name = person_list[5]
user=api.get_user(username=person_name,
user_fields=['description','protected','name','username','public_metrics','profile_image_url']
,user_auth=True)
tweets = api.get_users_tweets(user.data.id, max_results=100,exclude=['retweets', ],\
tweet_fields=['created_at', ],until_id = None, user_auth=True,)
# ファイルを保存
with open(f'ディレクトリ/tweet_{person_name}_1.csv', 'w', newline='') as f:
writer = csv.writer(f)
for tweet in tweets.data:
writer.writerow([tweet.created_at, tweet.text, tweet.id])
<コード2>
1回目の実行で取得した100件目のツイートidを基に、残りの過去の期間のツイートを取得していきます。
※取得したツイートが3200件を超えるとエラーが出ます。
# 対象アカウントの決定
person_list = ["WSJMarkets","IBDinvestors","benzinga", "Investopedia"]
person_name = person_list[3]
user=api.get_user(username=person_name,
user_fields=['description','protected','name','username','public_metrics','profile_image_url']
,user_auth=True)
# 次のuntil_idを取り出す関数の定義
def road_csv(df):
next_id = df.iloc[-1, 2]
return (next_id)
# ツイートを取得する関数を定義
def get_tweets(next_id):
tweets = api.get_users_tweets(user.data.id, max_results=100,exclude=['retweets', ],\
tweet_fields=['created_at', ],until_id = next_id, user_auth=True,)
return tweets
# ツイートをCSVに書き込む関数の定義
def save_csv(tweets, i):
with open(f'ディレクトリ/tweet_{person_name}_{i+1}.csv', 'w', newline='') as f:
writer = csv.writer(f)
for tweet in tweets.data:
writer.writerow([tweet.created_at, tweet.text, tweet.id])
return
# 連続で過去のツイートを取得する
for i in range(1,31):
df_tweet = pd.read_csv(f"ディレクトリ/tweet_{person_name}_{i}.csv")
next_id = road_csv(df_tweet)
tweets = get_tweets(next_id)
save = save_csv(tweets, i)
取得したツイートの一部を下記に示します。
A列がツイート日時、B列がツイート本文、C列がツイートidを表しています。
ファイルはcsv形式で保存しました。

4. データの前処理
4.1 ツイートの加工
学習データを作成するために、以下の手順で取得したツイートに対するネガポジ分析を行い、日付けごとのPN値の平均値を求めます。
ネガポジ分析を行うことで、ツイートが前向きか後ろ向きな発言なのかを定量的に判定することが可能となります。
※PN値:Positive Negative Valueの略。-1に近いほどnegative、+1に近いほどpositiveであることを示します。
出展:単語感情極性対応表
<コード3>
必要なモジュールをインストールします。
ネガポジ分析を行うためには、ツイート(文章)に対して形態素解析を行い、個々の品詞に分割します。
それぞれの品詞を単語感情極性対応表と照らし、該当する語句のPN値を取得します。
日本語の形態素解析には一般的に「MeCab」といったモジュールが使用されますが、今回対象とする言語が英語のため、多言語の自然言語処理を実施可能なPolyglotを使用することとしました。以下にpolyglotに関する情報と使用したデータセットを示します。
- Polyglot:約70言語の自然言語処理を実行可能。ここでは英文の形態素解析に使用する。
- pycld2:Googleが提供する、Python向けの言語検出ライブラリ。与えられたテキストの言語を判定する。
- embeddings2.en:英語の単語埋め込み辞書。単語を数値ベクトルで表現するために必要となるデータセット。
- pos2.en:英語の品詞タグ付けリソース。各英単語に対応する品詞をまとめている。
!pip install polyglot
!pip install pycld2
!polyglot download embeddings2.en
!polyglot download pos2.en
※Google Colaboratolyでは一定時間が経過すると接続が切れるため、その度にモジュールのインストールを実行する必要があります。
<コード4>
使用するモジュールをインポートします。
from pandas.core.tools.datetimes import to_datetime
from datetime import datetime as dt
from polyglot.text import Text
import pandas as pd
import numpy as np
import glob
import pytz
import pycld2
<コード5>
極性辞書を読み込み、各単語に対応するPN値を辞書型リストに格納します。
※Word:単語、POS:品詞、PN:PN値
# 極性辞書の読み込み、及び単語ごとの極性情報の整理
pn_df = pd.read_csv("ディレクトリ/pn_en.dic",\
sep=":",
encoding="utf-8",
names = ("Word","POS","PN"))
word_list = list(pn_df["Word"])
pn_list = list(pn_df["PN"])
pn_dict = dict(zip(word_list, pn_list))
POS(品詞)は略称で示されています。
こちらのサイトから略称と品詞の対応関係を確認することができます。
pandasの.head()を使用することで、上記のようにデータフレームの先頭5行のみを抽出することが出来ます。
<コード6>
取得したツイートに対してネガポジ分析を実施します。ツイートは同じ日にち内で複数存在するため、その日の各ツイートのPN値の平均値を使用することとしました。
ツイートに英語以外の言語が含まれることでエラーが生じたため、pycld2でツイートが英語の時のみに形態素解析を行うように工夫しました。
# 形態素解析を行い、文書中からBaseFormを取り出す関数を定義
def get_diclist(text):
diclist = [] # {"BaseForm":取得した単語}を格納するリスト
# ツイート中のhttps以降は不要のため削除
if "https" in text:
pos = text.find("https")
text = text[:pos]
# 入力言語が英語であれば形態素解析を実施
is_reliable, text_bytesFound, details = pycld2.detect(text)
if "en" == details[0][1]:
# 形態素解析を実施
tokens = Text(text)
parsed = tokens.pos_tags
# BaseFormを抽出
for i in parsed:
d = {"BaseForm": i[0]}
diclist.append(d)
# 対象テキストが英語でない場合は"None"を入力
else:
diclist.append({"BaseForm":"0"})
return diclist
# BaseFormごとのPN値を求める関数を定義
def add_pnvalue(diclist_old, pn_dict):
diclist_new = [] # {"BaseForm":word, "PN値":pn_value}を格納する
for word in diclist_old:
base = word["BaseForm"]
if base in pn_dict:
pn = float(pn_dict[base])
else:
pn = "notfound"
word["PN"] = pn
diclist_new.append(word)
return diclist_new
# 1ツイートのPN値の平均値を求める
def get_mean(diclist_new):
pn_list = []
for word in diclist_new:
pn = word["PN"]
if pn != "notfound":
pn_list.append(pn)
if len(pn_list) > 0:
pnmean = np.mean(pn_list)
else:
pnmean = 0
return pnmean
# 日付けを文字列からdatetimeオブジェクト(datetime.datetime)に変換する関数を定義
def change_date(dates):
dates = pd.to_datetime(dates)
dates_r = dates.dt.tz_convert("America/New_York")
return dates_r
df_list = [] # 各データフレームを格納するリスト
# GooglDriveからツイートが格納されたファイルを読み込み、df_listにまとめる
tweets_list = ["WSJMarkets", "IBDinvestors", "benzinga", "Investopedia"] # 他のアカウントのツイートを追加可能
for acount in tweets_list:
files = glob.glob(f"ディレクトリ/tweet_{acount}_*.csv")
for file in files:
df_tweet_file = pd.read_csv(file, header=None) # 元データにカラム名が設定されていないためNoneを指定
# カラム名を設定
labels = ["Day", "tweet", "tweet_id"]
labels_dict = {num: label for num, label in enumerate(labels)}
df_tweet_file = df_tweet_file.rename(columns=labels_dict)
df_tweet_file = df_tweet_file.drop("tweet_id", axis=1) # tweet_idは使用しないため削除
# グリニッジ標準時をニューヨークの時間に補正する(時差は約5時間。アメリカが遅れている。)
dates = df_tweet_file["Day"]
df_tweet_file["Day"] = change_date(dates)
# df_listに取得したDFを追加する
df_list.append(df_tweet_file)
# df_list中の各DFを一つに統合する
df_all = pd.concat(df_list, axis=0)
# df_allの1tweetごとのPN値を求める
pn_mean_list = []
for i in range(0,len(df_all.axes[0])):
tweet = df_all.iloc[i, 1]
diclist = get_diclist(tweet)
diclist_new = add_pnvalue(diclist, pn_dict)
pnmean = get_mean(diclist_new)
pn_mean_list.append(pnmean)
df_all["pn"] = pn_mean_list # df_allにツイートのPN値を追加
df_all = df_all.drop("tweet",axis=1) # df_allからツイートカラムを削除
df_all = df_all.sort_values(by="Day", ascending=True) # 日付けで昇順に並び替える
# 使用するデータ範囲を設定
dates = {"date":[dt(2022,10,1), dt(2023,1,31)]}
df_dates = pd.DataFrame(dates)
tz = pytz.timezone('America/New_York')
df_dates["date"] = pd.to_datetime(df_dates["date"]).dt.tz_localize(tz)
start = df_dates.iloc[0,0] # データ取得開始日
end = df_dates.iloc[1,0] # データ取得終了日
# 指定した期間のデータのみを抽出
mask = (df_all["Day"] >= start) & (df_all["Day"] <= end)
df_all = df_all.loc[mask]
# 日付けをインデックスに設定
df_all = df_all.set_index("Day")
# 日ごとのPN値の平均値を求める
df_all = df_all.resample("1D").mean()
df_allの中身は以下の通りです。
4.2 株価データの加工
株価としてはS&P500指数を採用しました。
ファイルは次ような表形式で整理されているため、学習に用いる終値のみを取得します。

株価データは以下のサイトからcsv方式でダウンロードすることが出来ます。
出展:Investing.com
<コード7>
前日とのPN値、及び株価の変動をグラフにして両者の傾向を確認します。
株価データの日付けのデータ型をdf_allと整合させるためにタイムスタンプ型に変換します。
# 株価データの読み込み
df_chart = pd.read_csv("ディレクトリ/S&P 500 Historical Data.csv")
# .to_datetime()により、日付けのデータ型をタイムスタンプ型に変更する。
tz = pytz.timezone('America/New_York')
df_chart["Date"] = pd.to_datetime(df_chart["Date"]).dt.tz_localize(tz)
df_chart = df_chart.drop(["Open","High","Low","Vol.","Change %"],axis=1)
df_chart = df_chart.sort_values(by="Date", ascending=True) # 日付けで昇順に並び替える
# 使用するデータ範囲を設定
dates = {"date":[dt(2022,10,1), dt(2023,1,31)]}
df_dates = pd.DataFrame(dates)
df_dates["date"] = pd.to_datetime(df_dates["date"]).dt.tz_localize(tz)
# 任意の期間のデータのみを抽出
start = df_dates.iloc[0,0] # データ取得開始日
end = df_dates.iloc[1,0] # データ取得終了日
mask_2 = (df_chart["Date"] >= start) & (df_chart["Date"] <= end)
df_chart = df_chart.loc[mask_2]
# 日付けをインデックスに設定
df_chart = df_chart.set_index("Date")
# 株価データとPN値を内部結合する
df_table = df_all.join(df_chart, how="inner")
# Dateをカラムとして再設定
df_table.reset_index(inplace=True)
df_table = df_table.rename(columns={"index":"Date"})
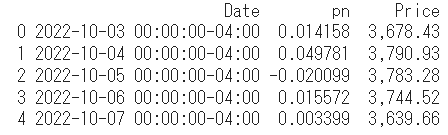
以下に作成したdf_tableを示します。
無事に日付けごとのPN値と株価を整理することが出来ました。
※pn:PN値、Price:終値
4.3 訓練用データと検証用データの作成
4.2で作成したdf_tableを基に、機械学習モデル作成のための訓練データ、及び検証用のデータを作成していきます。
流れを以下に示します。
1. データを8:2で分割し、訓練用データと検証用データを作る。
2. 訓練用データ→検証用データの順で、前日と次の日のPN値、株価の差分を求める。
3. PN値、株価それぞれの差分をグラフとして可視化する。
4. 両者の差分を3日間ごとにまとめる。対応するラベルデータとして、株価が前日と比べて上がった場合は「1」、下がった場合は「0」を充てる。
<コード8>
それでは、最初に全データを訓練用と検証用に分割します。
x = df_table.values[:,1] # pn値を説明変数とする
y = df_table.values[:,2] # 株価を教師データ
# データを学習用と検証に8:2に分割
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.2, random_state=0, shuffle=False)
# pn値データを標準化する
x_train_std = (x_train - x_train.mean()) / x_train.std()
x_test_std = (x_test - x_test.mean()) / x_test.std()
# 訓練データとテストデータの作成
df_train = pd.DataFrame({"pn":x_train_std, "Price":y_train}, columns=["pn", "Price"],\
index=df_table["Date"][:len(x_train_std)])
df_test = pd.DataFrame({"pn":x_test_std, "Price":y_test}, columns=["pn", "Price"],\
index=df_table["Date"][len(x_train_std):])
訓練用、検証用データを標準化し、それぞれ以下の形式で整理することが出来ました。
なお、訓練用データは65日分、検証用データは17日分あります。
機械学習では、65日分のデータを基に予測モデルを構築し、残りの17日分のデータを使って、モデルの性能としての正答率を確認します。

<コード9>
訓練用データと検証用データを学習用にさらに加工していきます。
コード8では、PN値、株価を時系列で並べていました。
コード9では、前日と当日のPN値、株価の差分を求めグラフで対応関係を確認します。
"""
訓練用データの加工
"""
exchange_dates = [] # 日付けを格納するリストを用意
pn_rates = []
pn_rates_diff = [] # 1日ごとのPN値の差分を格納するリストを用意
exchange_rates = []
exchange_rates_diff = [] # 1日ごとの株価を格納するリストを用意
prev_pn = df_train["pn"][0] # PN値カラムの最初の値を指定
prev_exch = float(df_train["Price"][0].replace(",","")) # 株価カラムの最初の値を指定
# 訓練データの個数分、PN値と株価の変化を算出し、exchange_dates, pn_rates_diff, exchange_rates_diffに追加していく
for i in range(len(x_train_std)):
# 日にちごとのPN値、株価を順番に抽出する
time = df_train.index[i]
pn_val = df_train["pn"][i]
exch_val = float(df_train["Price"][i].replace(",",""))
# 上記で抽出した日にちごとのPN値と株価の値それぞれの差分、及び対応する日付けをそれぞれのリストに追加する
exchange_dates.append(time)
pn_rates_diff.append(pn_val - prev_pn) # 1日前のPN値と現在のPN値の差分を求める
exchange_rates_diff.append(exch_val - prev_exch) # 1日前の株価と現在の株価の差分を求める
# 次の差分を求めるために、prev_pnとprev_exchを更新する
prev_pn = pn_val
prev_exch = exch_val
# 横軸を時間として、PN値、株価のそれぞれをグラフで可視化する
fig = plt.figure(figsize=(6,8))
ax1 = fig.add_subplot(2,1,1)
ax2 = fig.add_subplot(2,1,2)
x_val = exchange_dates # 横軸の時間を設定
y_val = pn_rates_diff # 縦時期のPN値の差分を設定
y_val_ex = exchange_rates_diff
# ax1のグラフの作成(PN値の差分の時系列)
ax1.set_title("PN Value (diff)")
ax1.plot(x_val, y_val)
ax1.grid(True)
plt.setp(ax1.get_xticklabels(), rotation=30)
# ax2のグラフの作成(株価の差分の時系列)
ax2.set_title("Price Valus(diff)")
ax2.plot(x_val, y_val_ex)
ax2.grid(True)
plt.setp(ax2.get_xticklabels(), rotation=30)
plt.show()
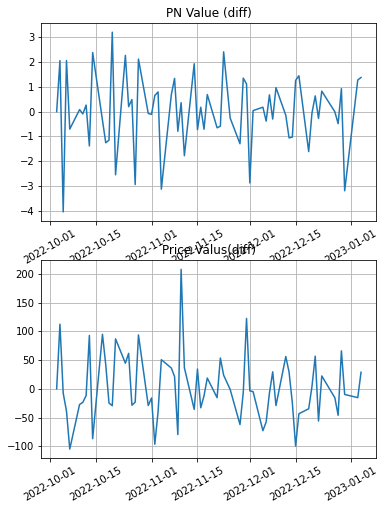
PN値、株価について、前日との差分を示したグラフを下記に示します。
<コード10>
次に、PN値、株価の前日の差分データ(pn_rates_diff、exchange_rates_diff)を3日間ごとにまとめます。
整理した後の一部を以下に示します。
[ 6.60600000e+01 9.29394997e-01 -9.78000000e+00 -3.19313034e+00 -1.53600000e+01 1.27811787e+00]
コード10を実行すると、上記リストの「0番目に株価差分、1番目にPN値差分」と交互に計6つのデータ(株価3日分、PN値3日分)が1つのリストに挿入されます。
これを説明変数とします。
目的変数である株価についても整理します。
株価の場合は、前日と当日の差分が0以上の場合は「1」、そうでない場合は「0」として変換します。これを目的変数とします。
下記はtrain_label_arrの中身です。
[0 0 0 0 0 1 0 1 1 0 0 1 1 1 0 0 1 0 0 0 0 1 1 1 0 1 1 0 1 0 0 1 0 1 1 0 0 0 1 0 0 0 0 0 1 0 1 1 0 0 0 0 1 1 0 1 0 0 1 0 0 1]
データは全部で62個あり、1の個数が25個で全体の4割程度、0の個数が37個で全体の6割程度を占めています。
なお、検証用データは14個あり、1が6つ、0が8つ含まれています。
"""
訓練用データの加工(続き)
"""
# 次に、3日間ごとにデータをまとめていく
INPUT_LEN = 3
data_len = len(pn_rates_diff) # pn_rates_diffのデータの個数
tr_input_mat = [] # 学習データを格納するリスト
tr_angle_mat = [] # 教師データを格納するリスト
# データを1つずつずらして、3日間ごとにまとめていく
# 3日間ごとの株価とPN値の変化に対応した株価の上下(上がったら1、下がったら0)を作成する
for i in range(INPUT_LEN, data_len):
tmp_arr = [] # 3日間ごとの値を格納するリスト
# PN値も株価も同じリストに追加していく
for j in range(INPUT_LEN):
tmp_arr.append(exchange_rates_diff[i - INPUT_LEN + j]) # (1,2,3), (4,5,6)のようなまとまりが作られる
tmp_arr.append(pn_rates_diff[i - INPUT_LEN + j]) #i=3の時、(1,2,3), i=4の時、(2,3,4)
tr_input_mat.append(tmp_arr) # [[e1,p1,e2,p2,e3,p3],[e2,p2,e3,p3,e4,p4],,, ]のようなリスト形式になる
# 前日との株価の変化を格納したリストexchange_rates_diffについて、プラスなら1,マイナスなら0を出力する
if exchange_rates_diff[i] >= 0:
tr_angle_mat.append(1)
else:
tr_angle_mat.append(0)
# 訓練用データ
train_feature_arr = np.array(tr_input_mat) #作成した学習データ
train_label_arr = np.array(tr_angle_mat) #作成した教師データ
検証用データについても、上記と同様に説明変数、目的変数のそれぞれを整理していきます。
<コード11>
"""
検証用データの加工
"""
prev_pn_test = df_test["pn"][0]
prev_exch_test = float(df_test["Price"][0].replace(",",""))
exchange_dates_test = [] # 日付けを格納するリスト
pn_rates_test = []
pn_rates_diff_test = []
exchange_rates_test = []
exchange_rates_diff_test = []
for i in range(len(x_test_std)):
time = df_test.index[i]
pn_val = df_test["pn"][i]
exch_val = float(df_test["Price"][i].replace(",",""))
exchange_dates_test.append(time)
pn_rates_diff_test.append(pn_val - prev_pn_test)
exchange_rates_diff_test.append(exch_val - prev_exch_test)
prev_pn_test = pn_val
prev_exch_test = exch_val
data_len = len(pn_rates_diff_test)
test_input_mat = []
test_angle_mat = []
for i in range(INPUT_LEN, data_len):
test_arr = []
for j in range(INPUT_LEN):
test_arr.append(exchange_rates_diff_test[i - INPUT_LEN + j])
test_arr.append(pn_rates_diff_test[i - INPUT_LEN + j])
test_input_mat.append(test_arr)
if exchange_rates_diff[i] >= 0:
test_angle_mat.append(1)
else:
test_angle_mat.append(0)
# 検証用データ
test_feature_arr = np.array(test_input_mat)
test_label_arr = np.array(test_angle_mat)
5. 機械学習モデルの実装と予測結果の評価
上記の操作により、訓練データとして「train_feature_arr、train_label_arr」、検証用データとして「test_feature_arr、test_label_arr」をnumpy配列形式で得ることが出来ました。
これらのデータを使用して予測モデルを構築していきます。
今回は、データ分析講座で学習したモデルのうち、以下のモデルを使用しました。
- k近傍法(k-NN)
- ロジスティック回帰
- 線形SVM
- 非線形SVM
- 決定木
- ランダムフォレスト
はじめに、パラメータを調整しない場合の正答率を確認します。
<コード12>
パラメータとしてランダムに変化する値を含む場合、計算を実行するごとに結果が変化しないよう、random_state=42で乱数を固定しました。
線形SVMモデルについては、デフォルトのパラメータセットでは計算が収束しない旨を知らせるメッセージが表示されたため、メッセージを回避するために(C=0.01,max_iter=10000, random_state=42)を用いました。
from sklearn.neighbors import KNeighborsClassifier # k近傍法(k-NN)
from sklearn.linear_model import LogisticRegression # ロジスティック回帰
from sklearn.svm import LinearSVC # 線形SVM
from sklearn.svm import SVC # 非線形SVM
from sklearn.tree import DecisionTreeClassifier # 決定木
from sklearn.ensemble import RandomForestClassifier # ランダムフォレスト
models = [KNeighborsClassifier(), LogisticRegression(random_state=42), LinearSVC(C=0.01,max_iter=10000, random_state=42),\
SVC(random_state=42), DecisionTreeClassifier(random_state=42), RandomForestClassifier(random_state=42)]
num = [0,1,2,3,4,5]
model_diclist = dict(zip(num, models))
accuracy = {} # 正答率を格納する辞書型リスト
for i, model in enumerate(models):
model.fit(train_feature_arr, train_label_arr)
score = model.score(test_feature_arr, test_label_arr)
model_name = model.__class__.__name__
accuracy[model_name] = score
print("--Method:", model_name, "--")
print("Test score:{}".format(score))
print()
# 正答率の高い順にモデルを並び替える
accuracy = dict(sorted(accuracy.items(), key=lambda x:x[1], reverse=True))
keys_list = list(accuracy.keys())
values_list = list(accuracy.values())
# 棒グラフを出力
fig, ax = plt.subplots()
bars = ax.bar(keys_list, values_list)
# 棒グラフ上部に正答率を表示する
for bar in bars:
height = bar.get_height()
ax.text(bar.get_x() + bar.get_width()/2., height, float(round(height, 2)), ha="center", va="bottom")
# 正答率を可視化
plt.xlabel("model_number")
plt.xticks(rotation = 80)
plt.ylabel("accuracy")
plt.title("accuracy of each model_rev1")
plt.ylim(0,1)
plt.show()
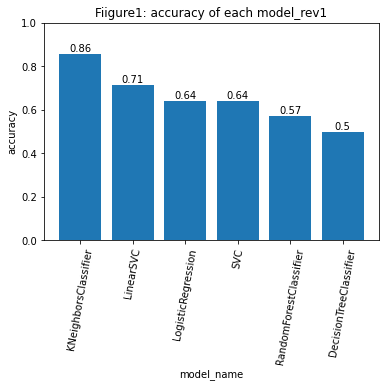
パラメータを調整しない場合の正答率はFigure1に示す値となりました。
計算の結果、k近傍法が最も高い正答率を示す結果となりました。
Figure1では、線形SVMを除いて各パラメータについてデフォルト値を使用しました。
次に、パラメータの最適化手法の一つであるグリッドサーチを使用し、正答率の向上を試みます。
グリッドサーチでは、パラメータに対して任意の幅を与え、一つずつパラメータの組み合わせを作り、組み合わせごとに計算を行います。
複数の計算結果の中から、最終的に評価指標として選定した値が最も高い組み合わせを選ぶことが出来ます。
今回は正答率を指標として選びました。
他にパラメータの最適化手法にはランダムサーチと呼ばれる手法があります。こちらは任意のパラメータの幅から確率的に値を取り出し、パラメータの組み合わせを決定します。
パラメータの最適化手法と合わせて交差検証も実装します。
交差検証を使用することで、特定の訓練データに過剰にモデルが適合する過学習の影響を小さくできます。今回使用するデータは時系列データのため、時系列交差検証を使用しました。
交差検証の詳細については下記のサイトをご確認ください。
交差検証(Python実装)を徹底解説!図解・サンプル実装コードあり
<コード13>
コード13では、モデルをより詳細に評価するために、正答率が最も高かった時の適合率(precision)、再現率(recall)、F1値(F1-score)、そして混同行列も求めます。
from sklearn.neighbors import KNeighborsClassifier # k近傍法(k-NN)
from sklearn.linear_model import LogisticRegression # ロジスティック回帰
from sklearn.svm import LinearSVC # 線形SVM
from sklearn.svm import SVC # 非線形SVM
from sklearn.tree import DecisionTreeClassifier # 決定木
from sklearn.ensemble import RandomForestClassifier # ランダムフォレスト
from sklearn.model_selection import GridSearchCV, TimeSeriesSplit
from sklearn.metrics import accuracy_score
from sklearn.metrics import precision_score
from sklearn.metrics import recall_score
from sklearn.metrics import f1_score
from sklearn.metrics import confusion_matrix
# 使用モデル一覧
KNN = KNeighborsClassifier()
LR = LogisticRegression()
LSVC = LinearSVC()
SVC = SVC()
DTC = DecisionTreeClassifier()
RFC = RandomForestClassifier()
models = [KNN, LR, LSVC,SVC, DTC, RFC]
# モデルごとのパラメータセット
KNN_model_param = {KNN: {"n_neighbors": list(range(1, 8)), "leaf_size": [i for i in range(10, 51)]}}
LR_model_param = {LR:{ "C": [10 ** i for i in range(-4, 5)], "random_state": [42]}}
LSVC_model_param = {LSVC: {"loss": ["hinge","squared_hinge"], "C": [10 ** i for i in range(-4, -2)],"max_iter":[10000] , "random_state": [42]}}
SVC_model_param = {SVC: {"kernel": ["linear", "poly", "rbf", "sigmoid"], "C": [10 ** i for i in range(-3, 1)], "random_state": [42]}}
DT_model_param = {DTC: {"max_depth": [i for i in range(1, 50)], "random_state": [42]}}
RF_model_param = {RFC: {"n_estimators": [i for i in range(1, 21)], "max_depth": [i for i in range(1, 10)], "random_state": [42]}}
# モデル・パラメータセット
param_set = [KNN_model_param, LR_model_param, LSVC_model_param, \
SVC_model_param, DT_model_param, RF_model_param]
accuracy_dic_3 = {} # モデルごとに正答率の最大値を格納するリスト
precision_dic_3 = {} # 適合率を格納するリスト
recall_dic_3 = {} # 再現率を格納するリスト
f1_dic_3 = {} # F1値を格納するリスト
param_dic_3 = {} # 最も正答率が高かった時のパラメータを格納するリスト
# 時系列交差検証のための分割数を設定
tscv = TimeSeriesSplit(n_splits=15, max_train_size = None)
# グリッドリサーチの実施
for model_param_set_grid in param_set:
max_accuracy = 0
max_precision = 0
max_recall = 0
max_f1 = 0
best_param = None
# 混同行列用に予測結果を格納するリスト
pred = []
pred_dic = {}
for model, param in model_param_set_grid.items():
clf = GridSearchCV(model, param, cv=tscv)
clf.fit(train_feature_arr, train_label_arr)
pred_y = clf.predict(test_feature_arr)
model_name = model.__class__.__name__
accuracy = accuracy_score(test_label_arr, pred_y)
precision = precision_score(test_label_arr, pred_y)
recall = recall_score(test_label_arr, pred_y)
f1 = f1_score(test_label_arr, pred_y)
# 正答率が最も高かった時のprecision, recall, f1を確認する。
if max_accuracy < accuracy:
max_accuracy = accuracy
max_precision = precision
max_recall = recall
max_f1 = f1
# 正答率が最も高かった時の予測結果
pred = pred_y
# 正答率が最も高かった時のパラメータセット
best_param = clf.best_params_
# 各モデルについて、グリッドサーチで最も正答率が良かった時の各評価指標を辞書に格納
accuracy_dic_3[model_name] = max_accuracy
precision_dic_3[model_name] = max_precision
recall_dic_3[model_name] = max_recall
f1_dic_3[model_name] = max_f1
param_dic_3[model_name] = best_param
pred_dic[model_name] = pred
# 混同行列の可視化
cm = confusion_matrix(test_label_arr, pred) # 正答率が最も高かった時の混同行列
print(f"confusion_matrix_{model_name}")
print(cm)
print("---accuracy---")
print(accuracy_dic_3)
print("---precision---")
print(precision_dic_3)
print("---racall---")
print(recall_dic_3)
print("---f1---")
print(f1_dic_3)
print("parameter_set")
print(param_dic_3)
実行の結果から求めた正答率をFigure2に、適合率、再現率、F1値をFigure3~5に示します。k近傍法が最も高い正答率を示しました。
他のモデルの正答率を確認すると、線形SVM、ロジスティック回帰、決定木の正答率はFigure1の結果と変わりませんでしたが、ランダムフォレストは0.57から0.71まで正答率を上げることが出来ました。
一方で、SVMの正答率は、0.64から0.57まで減少する結果となりました。
これは、SVMにおいて過学習が生じてしまったことが要因として考えられます。
SVMには”gamma”というパラメータが存在しますが、グリッドサーチに多くの時間を要するため、今回は外しています。gammaをグリッドサーチ時に考慮することで、正答率を向上させることが出来るかもしれません。
正答率のみを見れば、k-NNが最も良いモデルと判断できるかもしれませんが、正答率が高いからと言って良いモデルとは限らないため注意が必要です。作成したモデルが目的に見合ったものであるかを評価する必要があります。
目的に見合ったモデルであるかは、正答率を含めた次の4つの指標を基に考察することが出来ます。
1. 正答率(accuracy)
2. 適合率(precision)
3. 再現率(recall)
4. F1値(F1-score)
これらの指標を理解するためには、はじめに混合行列を理解する必要があります。
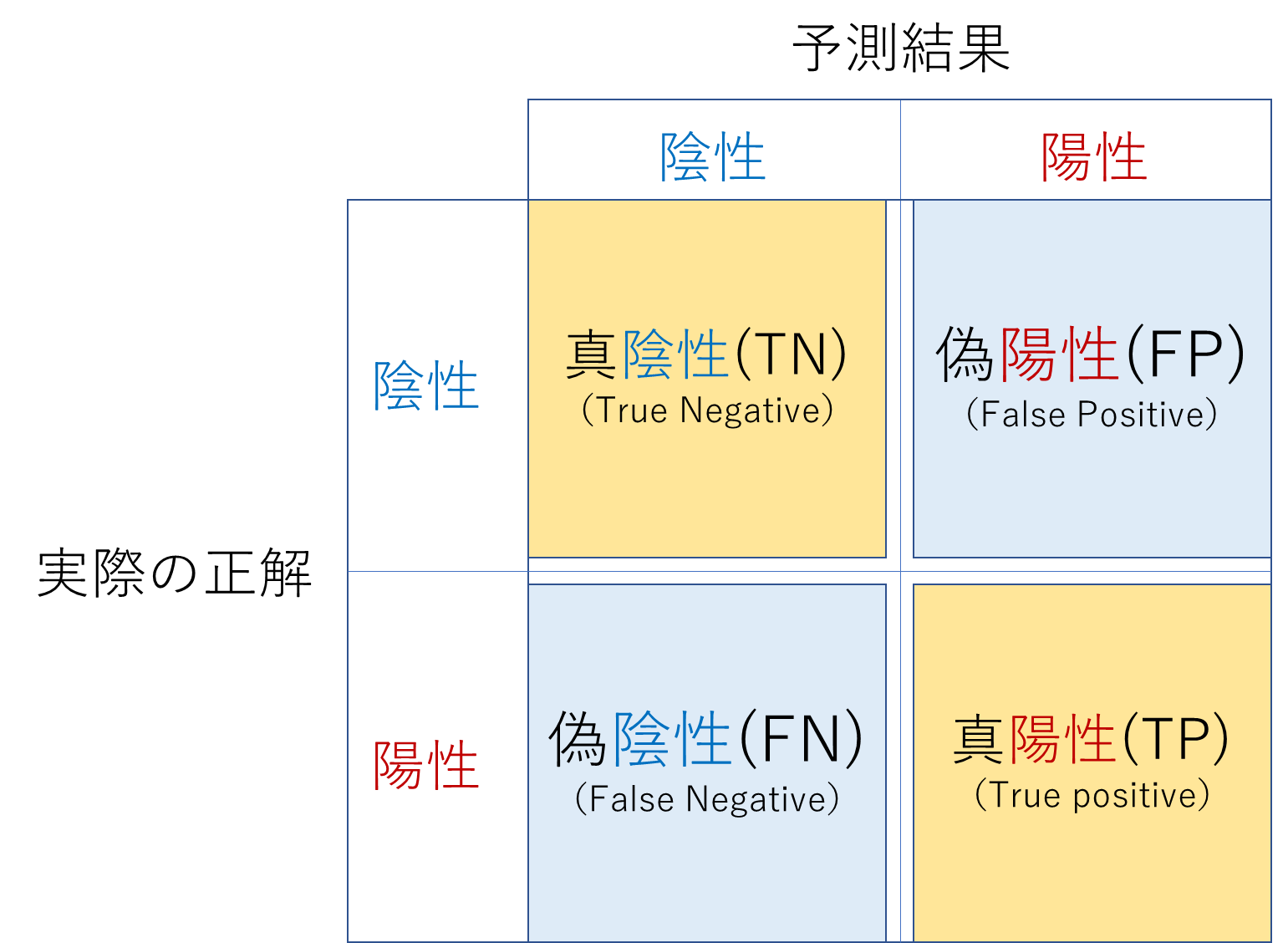
今回のように「株価が上がる(1)か、それとも下がる(0)のか」といった二値の分類問題においては、以下の図のように結果を整理することが出来ます。順番に見ていきます。ここでは陽性が株価の上昇(1)、陰性が株価の下落(0)を示しています。
- 真陽性(TP):真陽性は、実際に株価が上がり、かつ予測でも上昇を当てることができた状態です。
- 偽陽性(FP):偽陽性は、株価が上昇すると予測したものの、実際には株価が下落した状態です。
- 真陰性(TN):真陰性は、実際に株価が下がり、かつ予測でも下落を当てることが出来た状態です。
- 偽陰性(FN):偽陰性は、株価が下落すると予測したものの、実際には株価が上昇した状態です。
正答率、適合率、再現率、F1値は混同行列の上記の4つの要素から計算されます。
混同行列の概要を確認したところで、次にそれぞれの評価指標を確認していきます。
1. 正答率(accuracy)
正答率は、全体の要素の合計のうち、何回正しく株価の上昇と下落を予測できたのかを割合で示しています。
計算式は、次の通りです。この値が1に近づくほど、株価の上昇と下落を正しく予測できた回数が多いことになります。
accuracy = (TP+TN) / (TP+FP+TN+FN)
正答率が高かったとしても、真陰性の数が真陽性の数よりも多い場合、株価変動の予測に当てはめるとそのモデルは株価が下落するケースをより正確に判定できるモデルのため、株価上昇の予測には適していない可能性があります。
真陽性と真陰性の内訳は混同行列で確認することが出来ます。
グリッドサーチ後の各モデルの混同行列は次の通りです。

例えば、正答率が最も高かったk近傍法の真陽性は5つ、真陰性は7つ、検証用データの内訳は1が6つ、0が8つのため、比較的バランスの取れた予測を行うことが出来るモデルであると考えられます。
2. 適合率(precision)
適合率は、陽性、つまり株価が上昇すると予測したもののうち、実際に何回が正解であったかを割合で示しています。計算式は次の通りです。この値が1に近づくほど、株価が上昇すると予測した際に、それが正解であった割合が増えます。一方で、適合率が高い場合は再現率が低下するため、株価が上昇していたにもかかわらず、それを予測することが出来なかった割合(機会損失)が増える可能性が高くなります。ただし偽陰性が少ない場合はその限りではありません。
precision = TP / (TP+FP)
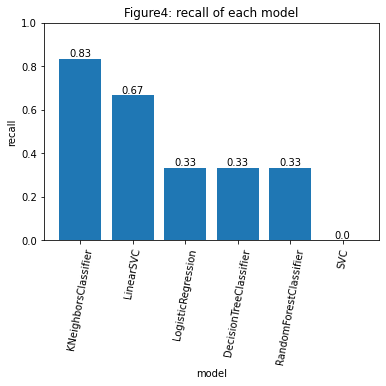
3. 再現率(recall)
再現率は、実際に株価が上昇した結果のうち、予測モデルで何回当てることが出来たのか割合で示しています。
計算式は次の通りです。この値が1に近づくほど、実際の株価の上昇を漏れなく予測できていることになります。一方で、再現率が高い場合は適合率が低下するため、株価の上昇を見逃す機会が減るものの、実際に上昇していなかった割合(誤検出)が増える可能性があります。ただし偽陽性が少ない場合はその限りではありません。
recall = TP / (TP+FN)
一般的に適合率と再現率はトレードオフの関係にあります。
株価の上昇を予測する場合、予測モデルの評価指標として再現率を用いてしまうと、株価の上昇を漏れなく捉えることのできる割合が増えます。その一方で、誤検出(予測で上昇すると予測したものの、実際には上昇しなかった割合)を増やすことになり、株価が下落するにもかかわらず新たに株式を購入してしまうケースが増えるかもしれません。
できるだけ損失を小さくし手堅く利益を得たい場合、今回構築した予測モデルの中では、株価の上昇を誤検出少なく予測可能なランダムフォレストを採用することが望ましいと考えられます。理由は適合度が1であるためです。
しかし、他社と利益を競っているような場面では利益を最大化することが目的となるため、再現率も重視しなければなりません。
その理由は、適合率のみを高めると株価が上昇した場面を見逃す機会が多くなる可能性があるためです。
実際に利益を最大化する場面でランダムフォレストを使用すると、ランダムフォレストの再現率は0.33であることから機会損失が多くなり、他社に総合的な利益で負ける可能性が高いです。
適合率と再現率の両方を重視する必要がある場合は、次のF1値が良い指標となります。
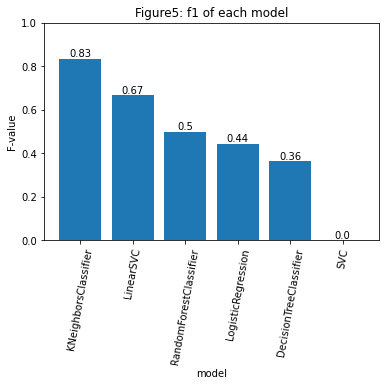
4. F1値(F1-score)
F1値は、適合率と再現率の両方をバランスよく考慮したい場合に用いる指標です。計算式は以下の通りで、適合率と再現率の調和平均をとっています。この値が1に近いほど、適合率と再現率の両方は高い値を示します。
F1score = 2 \times(precisoin\times recall) \div (precision + recall)
今回最も高いF1値を示したモデルは0.83でk近傍法でした。
そのため、機会損失をある程度回避し、利益を最大化するような場面ではk近傍法を用いることが良いと考えられます。
k近傍法の良さは教師データの状態からも判断できます。
Figure6は教師データの株価の上昇/下落の内訳を示したものです。

Figure6によると、株価の下落を示す教師データは上昇を示すデータよりも2割程度多くなっています。
通常このように教師データに偏りがある場合、モデルは割合の多い方を判定する回数が多くなります。
しかしk近傍法のF1値は0.83であり、適合率、再現率ともにバランスの取れたモデルとなっているため、実際に使用する場面で他のモデルよりもロバスト性を発揮できると考えられます。
6. まとめ
Aidemyの成果物として株価変動の予測モデル構築にチャレンジしました。
株価としてはS&P500を対象とし、学習データには米国の株式市場に関する情報を発信するTwitterアカウントと過去のS&P500のデータ約4カ月分を使用しました。
予測モデルの内容は、直近3日間のツイートのPN値と株価の変動から、次の日の株価の変動を予測するというものです。
機械学習モデルとしては、k近傍法、ロジスティック回帰、線形SVM,SVM,決定木、ランダムフォレストの5種類を使用しました。正答率、適合度、再現度、F1値のそれぞれを比較した結果、適合率ではランダムフォレスト、再現率とF1値ではk近傍法が最も高い値を示す結果となりました。
このことから、可能な限り損失を抑え、手堅く利益を得たい場合には適合率の高いランダムフォレスト、機会損失を減らし、利益の最大化を目指す場合にはf1値の大きいk近傍法をそれぞれ用いることが望ましいと考えました。
今後、Kaggleといったコンテストでも頻繁に使われるLightGBMやXGboostといった他のモデル、及び今回グリッドサーチの対象としなかった他のパラメータをパラメータ最適化に含めることで、より実用性のあるモデルに変えていきたいと思います。
合わせて、他のTwitterアカウントのツイートも含めた場合の挙動の変化も確認をしてみたいと思います。
最後まで御覧いただきありがとうございました。
7. 参考文献・サイト
【初心者向け】 機械学習におけるクラス分類の評価指標の解説
[評価指標]適合率(Precision、精度)とは?
[評価指標]再現率(Recall)/感度(Sensitivity)とは?
[評価指標]F値(F-measure、F-score)/F1スコア(F1-score)とは?
高村大也, 乾孝司, 奥村学
"スピンモデルによる単語の感情極性抽出", 情報処理学会論文誌ジャーナル, Vol.47 No.02 pp. 627--637, 2006.
Hiroya Takamura, Takashi Inui, Manabu Okumura,
"Extracting Semantic Orientations of Words using Spin Model", In Proceedings of the 43rd Annual Meeting of the Association for Computational Linguistics (ACL2005) , pages 133--140, 2005.