はじめに
直線や曲線を動かして領域を作成するという問題がある。高校数学のにおいて、これらの問題に対応するアプローチとして逆像法という解き方がある。そこで、今回はプログラミングを用いてそのような問題を解いたとき、どのような領域を図示することができるのか考察する。
問題
$x^2+y^2\le 1$を満たしてx,yが動くとき、(X,Y)=(x+y,xy)の動く領域を図示せよ。
解法1 逆像法
$X=x+y,Y=xy$としたとき、x,yを解に持つAの二次方程式は以下のように表すことができる。
A^2-XA+Y=0
ゆえに、この二次方程式が実数解を持つ条件は、
X^2-4Y\ge 0
一方で、$x^2+y^2=1$と対称式$x^2+y^2=(x+y)^2-2xy$から、
X^2-2Y\le1
ゆえに、
\frac{1}{2}X^2-\frac{1}{2} \le Y \le \frac{1}{4}X^2
解法2 三角関数と逆像法
$0\le r \le 1,0\le \theta \le 2\pi $としたとき、
\begin{equation}
\left\{ \,
\begin{aligned}
& x=r cos\theta \\
& y=r sin\theta \\
\end{aligned}
\right.
\end{equation}
となるx,yを設定する。
このとき、
\begin{equation}
\left\{ \,
\begin{aligned}
& X=x+y=r(cos\theta+sin\theta) \\
& Y=r^2 sin\theta cos\theta \\
\end{aligned}
\right.
\end{equation}
ここで、$\theta$を消去すると、
X^2=r^2+2Y
となる。
Y=\frac{1}{2}X^2-\frac{1}{2}r^2
したがって、
\frac{1}{2} X^2 -\frac{1}{2} \le Y \le \frac{1}{2}X^2 \tag{1}
ただし、三角関数において$\theta$を消去する過程において二乗の操作を行っているので、同値性が崩れてしまっている。そこで、$r=0$の場合と$r>0$の場合において$\theta$が存在するかを議論する必要性がある。
(1)$r=0$のとき
(X,Y)=(0,0)で$\theta$はすべての実数で条件を満たす。
(2)$r>0$のとき
\begin{equation}
\left\{ \,
\begin{aligned}
& cos\theta+sin\theta=\frac{X}{r} \\
& sin\theta cos\theta =\frac{Y}{r^2} \\
\end{aligned}
\right.
\end{equation}
これにおいて、実数$\theta$が存在する条件は、
t^2-(\frac{X}{r})t+(\frac{Y}{r^2})=0
のt解が$-1\le t\le 1$の範囲において存在することである。
f(t)=t^2-(\frac{X}{r})t+(\frac{Y}{r^2})
とおくと、これを満たすためには、判別式をDとおくと
\begin{equation}
\left\{ \,
\begin{aligned}
& D\ge 0 \\
& f(1)\ge 0 \\
& f(-1)\ge 0 \\
\end{aligned}
\right.
\end{equation}
ゆえに、
\begin{equation}
\left\{ \,
\begin{aligned}
& Y\le \frac{1}{4}X^2 \\
& Y\ge rX-r^2 \\
& Y\ge -rX-r^2 \\
\end{aligned}
\right.
\end{equation}
したがって、
\begin{equation}
\left\{ \,
\begin{aligned}
& Y\le \frac{1}{4}X^2 \\
& \frac{1}{4}X^2 \ge Y\ge rX-r^2 \\
&\frac{1}{4}X^2 \ge Y\ge -rX-r^2 \\
\end{aligned}
\right.
\end{equation}
ここで、
\frac{1}{4}X^2-(rX-r^2)=(\frac{1}{2}X-r)^2\ge 0
\frac{1}{4}X^2-(-rX-r^2)=(\frac{1}{2}X-r)^2 \ge 0
となるので、
Y\le \frac{1}{4}X^2 \tag{2}
さえ満たせば、同値性はクリアすることができる。また、(X,Y)=(0,0)も満たすので、$r=0$のときも内包している。
したがって、(1),(2)より
\frac{1}{2}X^2-\frac{1}{2} \le Y \le \frac{1}{4}X^2
プログラミング
以下のプログラムを作成した。
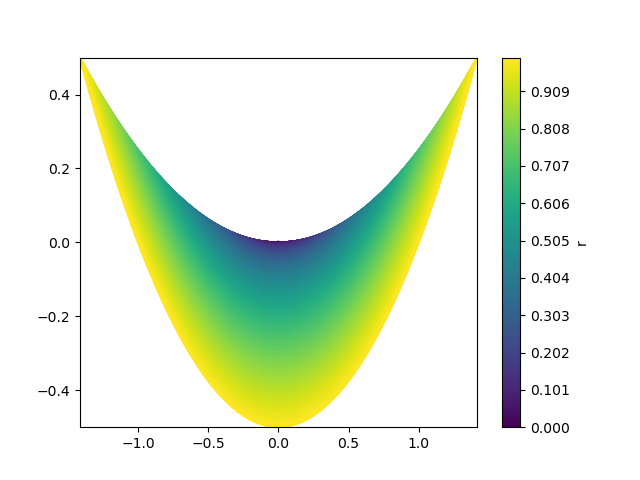
これは、解法2が元のアルゴリズムになっている。まずは、$r$に注目してみた
import numpy as np
import matplotlib.pyplot as plt
import math
n=1000
r=np.linspace(0,1,n)
theta=np.linspace(0,2*math.pi,n)
r,theta = np.meshgrid(r,theta)
x=r*np.cos(theta)
y=r*np.sin(theta)
X=x+y
Y=x*y
plt.contour(X,Y,r,n)
plt.colorbar(label="r")
plt.savefig("逆像法_r.png")
plt.show()
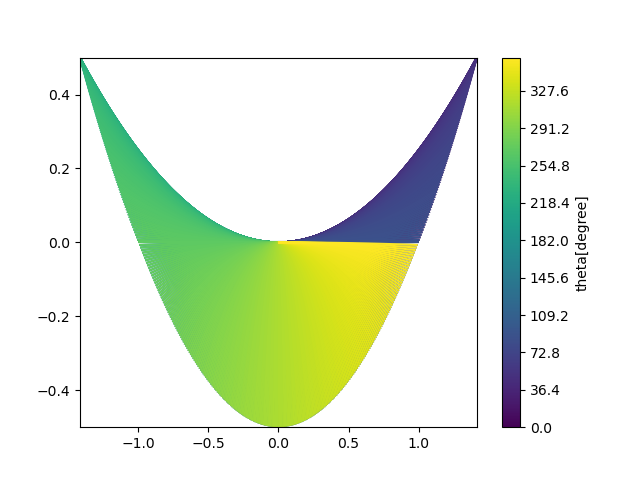
次に、$\theta$に注目してみた。
import numpy as np
import matplotlib.pyplot as plt
import math
n=1000
r=np.linspace(0,1,n)
theta=np.linspace(0,2*math.pi,n)
r,theta = np.meshgrid(r,theta)
x=r*np.cos(theta)
y=r*np.sin(theta)
X=x+y
Y=x*y
plt.contour(X,Y,theta*180/math.pi,n)
plt.colorbar(label="theta[degree]")
plt.savefig("逆像法_theta.png")
plt.show()
これを実行すると以下のような画像が出力される。
まとめ
逆像法を用いるときは、実数の存在条件をまずは考慮する必要がある。また、プログラムを用いて領域を図示することも直感的なアルゴリズムのプログラムを用いて作成可能であるということが分かった。
参考文献