はじめに
系統に並列接続される電力用コンデンサと高調波について考察する。パワエレ機器を接続すると系統に高調波電流が流れる。その場合、コンデンサのような高周波数領域でインピーダンスが激減する機器に高調波電流が流れる。そうするとコンデンサが熱により破損してしまう可能性がある。ゆえに、コンデンサに直列リアクトルを接続させることでコンデンサの破損を防ぐ。一方で、コンデンサ外部の系統に高調波電流をあまり流出させないといった効果も直列リアクトルは保持している。ここで、第五調波,第七調波に反応しやすいのは、6%リアクトルと13%リアクトルである。今回は、2つの直列リアクトルが系統に高調波を流出するのをどのように防いでいるのかを調査した。結果、以下のようなグラフになった。このグラフよりターゲットとなる高調波が外部に流出するのを直列リアクトルが防止してくれているということがわかる。
回路設定
単線結線図
以下に、今回調査する系統の単線結線図を載せる。
これから分かるように、高調波の発生源となる電流源から系統側と電力コンデンサ側に電流が分流していることが分かる。なので、配電系統側に流出する高調波電流を小さくするためには、分流比を上手く制御すればよいことが分かる。
等価回路
上記の考察により、以下のような等価回路を書くことが可能になる。
したがって、系統に流出してしまう高調波電流$I$は$I_{total}$を用いて以下のように表すことができる。(分流の式)
\dot{I}=\frac{jnX_L-\frac{1}{n}jX_C}{jX_1+(jnX_L-\frac{1}{n}jX_C)}I_{total}
プログラム
さて、$I$の式においてn(高調波の次数)を変化させた場合、どのような挙動を示すのか、プログラムによって解析したい。したがって、以下のようなプログラムを書いた。これは、6%と13%リアクトルの場合をそれぞれ示している。
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import math
m=10
f=50
omega = 2*math.pi*f
I_total=10
n=np.linspace(1,10,m)
#負荷側
X_1=10
X_C0=100
X_L1=X_C0*0.13
X_L2=X_C0*0.06
#電力用コンデンサ
X_C1= n*X_L1-(1/n)*X_C0
X_C2= n*X_L2-(1/n)*X_C0
I_1=abs((1j*X_C1)/(1j*X_1+1j*X_C1)*I_total)
I_2=abs((1j*X_C2)/(1j*X_1+1j*X_C2)*I_total)
plt.xlabel("高調波の次数")
plt.ylabel("負荷に流れる高調波電流")
plt.plot(n,I_1,color="red", label="13%")
plt.plot(n,I_2,color="blue", label="6%")
# 凡例表示
plt.legend(loc = 'upper right')
plt.savefig("高調波と電力用コンデンサと直列リアクトル.png")
plt.show()
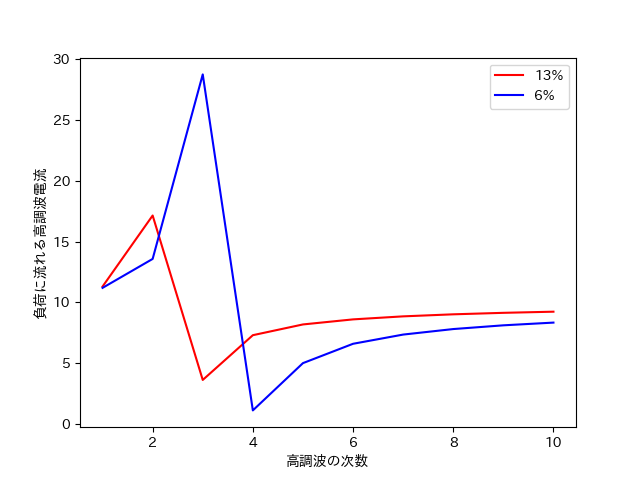
これを実行すると、以下のようなグラフが出力される。
このグラフから、ターゲットとなる次数周辺で系統に流出する高調波は減少するということが分かる。
まとめ
今回は、電力コンデンサに付随する直列リアクトルについて述べた。
直列リアクトルには、コンデンサの破損を防ぐ役割と外部系統にターゲット次数の高調波を流出させないという目的がある。今回は、後者の目的について、プログラムを用いることで検証した。結果、ターゲット次数の周辺では、系統に流出する高調波は減少するということが分かった。
参考文献