変圧器の規約効率と最大値について

はじめに

変圧器といった電気機器の運用効率を運転中に計測するのは難しい。そこで、あらかじめ変圧器の損失（負荷損、無負荷損）を別の手段で求めておいて、理論計算により効率を推定するという方法が多用される。このようにして求めた効率を規約効率といい、出力/入力=出力/(出力+入力)によって求めることができる。今回は、規約効率が最大になるときの条件を理論計算により求めた上でPythonを用いてグラフ化することを試みる。

規約効率の定義

導入

まず、変圧器とは入力された電力の電圧と電流を変成して出力する装置である。しかしもちろんのことながら、その変換過程において損失が生じてしまう。それは、ジュール熱による損失であり負荷に流れる電流の二乗に比例する負荷損と負荷に依存しない損失である無負荷損と大別することができる。

定義

そこで、全負荷時の負荷に流れる電流を$I$とし、負荷率$\alpha$,変圧器の銅線の抵抗成分を$r$とすると、銅損である負荷損は以下のように表すことができる。

P_c(\alpha)=(\alpha I)^2 r =\alpha^2I^2

ここで、出力を力率角$\theta$、系統電圧$V$で表すと、最大出力$P_{max}$は、以下のように表すことができる。

P_{max}=VIcos\theta

したがって、負荷率$\alpha$の時の出力$P(\alpha)$は以下のように表すことができる。

P(\alpha)=V(\alpha I)cos\theta =\alpha P_{max}=\alpha VIcos\theta

ゆえに、規約効率$\eta$は以下のように表すことができる。ただし$P_i$は固定損である無負荷損である。

\eta(\alpha)=\frac{\alpha VI cos\theta}{\alpha VI cos \theta +(\alpha I)^2 r +P_i}

規約効率の最大値

これの分子と分母を$\alpha$で除して、相加・相乗平均を用いると以下のようになる。

\eta(\alpha)=\frac{VIcos\theta}{VI cos\theta+\alpha I^2 r+P_i/\alpha}\le\frac{VIcos\theta}{VI cos\theta+2\sqrt{P_c P_i}}(\because{P_i=P_c})

このことから、銅損(負荷損)と鉄損(無負荷損)が等しいとき規約効率は最大になることが分かった。

プログラム

さて、このことについてPythonを用いてグラフ化してみよう。
負荷率を0から1まで変化させた時の効率[%]を求めるプログラムを書いた。

python efficient.py

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
fig, ax = plt.subplots()

I = 10
theta = 0
alpha = np.linspace(0,1,100)
V= 100
r=1.0

P_c = (alpha*I)**2*r
P_i = 10+0*alpha#定数配列と認識させるため

eta = (alpha*V*I*np.cos(theta)/(alpha*V*I*np.cos(theta)+P_c+P_i))*100

c1,c2,c3, = "blue","green","red",      # 各プロットの色
l1,l2,l3, = "効率","鉄損","銅損",   # 各ラベル

ax.set_xlabel('負荷率')  # x軸ラベル
ax.set_ylabel('効率・損失')  # y軸ラベル
ax.set_title("変圧器の効率[%]") # グラフタイトル
# ax.set_aspect('equal') # スケールを揃える
ax.grid()            # 罫線
#ax.set_xlim([-10, 10]) # x方向の描画範囲を指定
#ax.set_ylim([0, 1])    # y方向の描画範囲を指定
ax.plot(alpha, eta, color=c1, label=l1)
ax.plot(alpha, P_i, color=c2, label=l2)
ax.plot(alpha, P_c, color=c3, label=l3)

ax.legend(loc=0)    # 凡例
fig.tight_layout()  # レイアウトの設定
plt.savefig('変圧器の効率.png') # 画像の保存
plt.show()

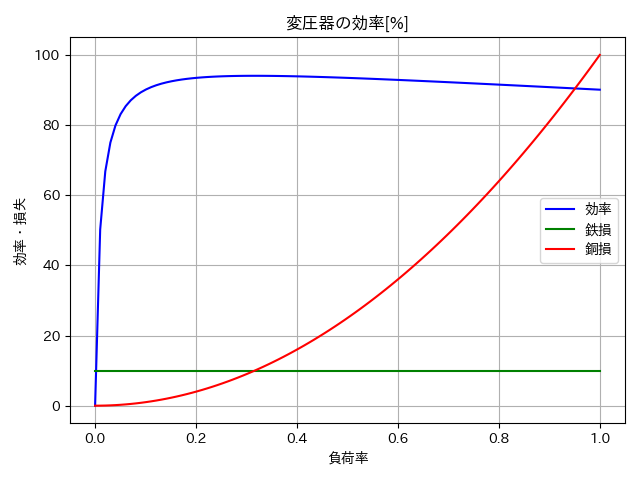
これを実行すると以下のような画像が出力される。確かに、無負荷損と負荷損が同じ大きさであるとき、効率が最大になるようである。

まとめ

今回は、変圧器の規約効率について定義を確認して、最大値を求めた。ただし、負荷損は、ジュール熱より負荷電流の2乗に比例する一方で、無負荷損は負荷電流に依存しないことを注意した。また、最大値を求めるためには、一般に微分法を用いるが、今回のような場合は、相加・相乗平均を用いて最大値を求めた。それにより、規約効率が最大になるのは、負荷損と無負荷損が等しくなるときであるということが分かった。また、負荷率を変化させていったとき、規約効率がどのように変化するのかをグラフ化するためにPythonを用いた。このような、最大・最小をグラフから求める問題は電気工学では頻出なので、しっかりと押さえておきたいところである。

参考文献