はじめに
数学において$sin(\frac{\pi}{7})$を求めることは、難しい。というのは、三角関数の加法定理を用いて計算を行おうとした場合、7次方程式を解く必要があるからである。ただし、手計算の工夫によっては3次方程式を解くだけでよい場合もある。そこで今回は、加法定理と二分法を用いることで7次方程式と同等の問題の解の近似値を推定する。これによって、$sin(\frac{\pi}{7})$の近似値を求める。
問題設定
以下のような方程式を考える。
x= sin(\frac{\pi}{7})
これの数値解析解を求めたい。三角関数の加法定理を用いて、
sin(\frac{7\pi}{7})(=f(x))
を$x$の式で表す。これは、7次多項式に相当する。
ここで、
f(x)=0
が成立する。これは7次方程式である。その解を遺伝的アルゴリズムを用いて推定する。ただし、上記方程式は$x=0$も解になってしまうことから、それを除外する。具体的には二分法の解の探索の範囲を$0.3<x<0.8$のような0よりも大きい範囲の探索に指定する。
三角関数の加法定理
概要
三角関数の加法定理は以下のように表すことができる。
sin(X+Y)=sin(X)cos(Y)+cos(X)sin(Y)
したがって、
x_n=sin(\frac{\pi n}{7})
という漸化式を考えると、
$\frac{n\pi}{7}<\frac{\pi}{2}$のとき、
x_{n+1}=x_n \sqrt{1-x^2}+ x_1 \sqrt{1-x_n^2}
もしくは、
$\frac{\pi}{2}<\frac{n\pi}{7}<\pi$のとき、
x_{n+1}=x_n \sqrt{1-x^2}+ x_1 (-\sqrt{1-x_n^2})
と表すことができる。ちなみにこれは、$cos$の正負のことを考慮している。
漸化式の妥当性(プログラム)
そこで、漸化式の妥当性を調査するべく以下のようなプログラムを書いた。
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import math
n=7
theta_1=math.pi/n
s_1=np.sin(math.pi/n)
c_1=(1-s_1**2)**0.5
theta_ary=[]
s_ary=[]
theta_ary.append(theta_1)
s_ary.append(s_1)
s=s_1
for i in range(1, n):
if theta_ary[i-1]<math.pi/2:
c_n=(1-s**2)**0.5
else:
c_n=-(1-s**2)**0.5
s = s*c_1+s_1*c_n
theta_ary.append(math.pi*(i+1)/n)
s_ary.append(s)
#print(s_ary[n-1])
plt.plot(theta_ary, s_ary)
plt.xlabel('θ')
plt.ylabel('sin(θ)')
plt.savefig('サインカーブの概形.png')
plt.show()
このプログラムを実行すると以下のようなサインカーブのような概形を描くことができる。
これは、
x_1=sin(\frac{\pi}{7})
の真の値(numpy)を用いて$x_7$までプロットした場合のグラフであるので、それがサインカーブに近い形をしているということは、漸化式が正しいということを示唆している。
二分法
7次方程式の定義
さて、
x_1=sin(\frac{\pi}{7})
とした場合、
f(x)=x_7=sin(\frac{7\pi}{7})=0
という7次方程式が成立することから、この方程式の『0よりも大きな』解を求めさえすれば、それが$sin(\frac{\pi}{7})$の値になるはずである。
二分法の概要
そこで、上記の7次方程式を二分法を用いて解くことを考える。
細かいアルゴリズムは以下のサイトを参照したい。
二分法では、2つの初期解$a,b$を用いて解を推定する。
以下簡単に概要を説明する。
まず、常識的に$a<x_{ex}<b$になりそうな$a,b$を経験的に定める。そうすると、その区間で関数$f(x)$が単調増加もしくは単調減少の関数と仮定した場合、
f(a)\times f(b)<0
が成立する。そこで、$c=\frac{a+b}{2}$となる中点を定める。
もし、
f(a)\times f(c)<0
ならば、解は区間[a,c]の間に存在する。一方で、
f(a)\times f(c)>0
ならば、解は[c,b]の間に存在する。このような操作を繰り返して解の存在範囲を限定していく方法を二分法という。
プログラム
以下のようなプログラムを作成した。
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import math
# sin(π/n)を求めたい
n=7
#解が存在していると思われる範囲の指定(0解を探索してしまうことを除外するため)
a=0.3
b=0.9
theta_1=math.pi/n
def sin_7_nibun(s_1):
#s_1=np.sin(math.pi/n)
c_1=(1-s_1**2)**0.5
theta_ary=[]
s_ary=[]
theta_ary.append(theta_1)
s_ary.append(s_1)
s=s_1
for i in range(1, n):
if theta_ary[i-1]<math.pi/2:
c_n=(1-s**2)**0.5
else:
c_n=-(1-s**2)**0.5
s = s*c_1+s_1*c_n
theta_ary.append(math.pi*(i+1)/n)
s_ary.append(s)
#print(s_ary[n-1])
return s_ary[n-1]
# 二分法
while True:
# 二分法の解の範囲指定
c=(a+b)/2
if sin_7_nibun(a)*sin_7_nibun(c)<0:
b=c
else:
a=c
# 終了条件
if abs(sin_7_nibun(c))<1.0*10**-5:
break
# sin(π/n)の推定値を表示
print(c)
# sin(π/n)の真値を表示
print(np.sin(math.pi/n))
# 誤差を計算
err= (abs(c-np.sin(math.pi/n))/np.sin(math.pi/n))*100
# 誤差のパーセントを表示
print(err)
これを実行すると、以下のような結果になる。
0.43388442993164067
0.4338837391175581
0.0001592164029825131
したがって、かなり高い精度で三角関数の値を求めていることが分かる。
誤差の推移
さて、推定値と真値の差より定義される誤差が、試行回数によってどのように変化するのかを調査するために、以下のようなプログラムを作成した。
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import math
# sin(π/n)を求めたい
n=7
#解が存在していると思われる範囲の指定(0解を探索してしまうことを除外するため)
a=0.3
b=0.9
theta_1=math.pi/n
err_ary=[]
i_ary=[]
i=0
def sin_7_nibun(s_1):
#s_1=np.sin(math.pi/n)
c_1=(1-s_1**2)**0.5
theta_ary=[]
s_ary=[]
theta_ary.append(theta_1)
s_ary.append(s_1)
s=s_1
for i in range(1, n):
if theta_ary[i-1]<math.pi/2:
c_n=(1-s**2)**0.5
else:
c_n=-(1-s**2)**0.5
s = s*c_1+s_1*c_n
theta_ary.append(math.pi*(i+1)/n)
s_ary.append(s)
#print(s_ary[n-1])
return s_ary[n-1]
# 二分法
while True:
i=i+1
# 二分法の解の範囲指定
c=(a+b)/2
if sin_7_nibun(a)*sin_7_nibun(c)<0:
b=c
else:
a=c
# 終了条件
if abs(sin_7_nibun(c))<1.0*10**-5:
break
# sin(π/n)の推定値を表示
##print(c)
# sin(π/n)の真値を表示
##print(np.sin(math.pi/n))
# 誤差を計算
err= (abs(c-np.sin(math.pi/n))/np.sin(math.pi/n))*100
# 誤差のパーセントを表示
##print(err)
err_ary.append(err)
i_ary.append(i)
# 誤差のグラフを表示
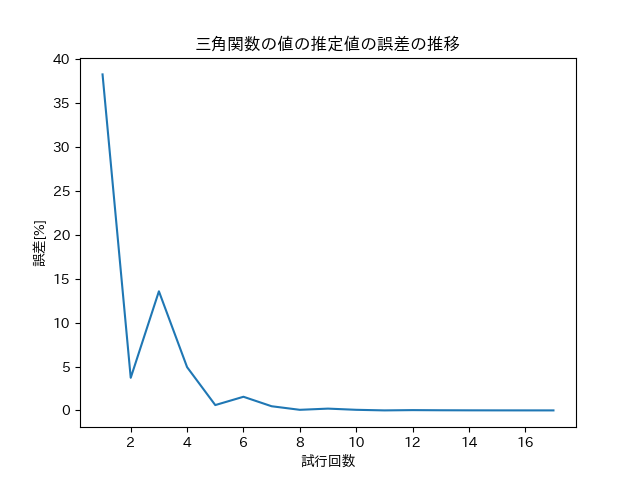
plt.title('三角関数の値の推定値の誤差の推移')
plt.plot(i_ary, err_ary)
plt.xlabel('試行回数')
plt.ylabel('誤差[%]')
plt.savefig('三角関数の値の推定値の誤差の推移.png')
plt.show()
このように、多少は振動するが試行回数を増加させるほどに誤差は小さくなっていくということが分かる。
まとめ
今回は、手計算では求めるのが難しい三角関数の値の近似値を高次方程式(漸化式)の近似解を求めることで推定した。具体的には、7次方程式の0よりも大きな解を二分法を用いることで推定した。二分法を用いるメリットは、推定解の範囲を人為的に指定することができるという点である。