はじめに
Pythonでは、matplotlibというライブラリが存在していて、それを用いることで2次元や3次元のグラフを描写することができる。ベクトルを描写するためにはquiver(x,y,u,v)という関数(x,y,u,vはベクトルを生成するためのパラメータ)を用いることでベクトルを1本ずつ描写することができる。一方で、streamplot(x,y,u,v)という関数を使えば、敷居は高いが、流れの場を描写することができる。今回は2つの関数を比較することによって、それぞれのメリットやデメリット、使用方法などを学習する。
また、補足として最後に電場を求める際に用いる微分の数値計算をプログラムによってできないかを考察した。そして、ライブラリの有無によって場合分けをした。
準備
まず、準備として、2次元のベクトル場、流れの場を描くためには、格子状の点の集合を用意する必要がある。したがって以下のようなプログラムをまずは書かなければならない。これは、等高線やコンター図のような曲面を描くときも同様である。
import matplotlib.pyplot as plt
import math
import numpy as np
import japanize_matplotlib
n=10
x=np.linspace(-1,1,n)
y=np.linspace(-1,1,n)
X,Y = np.meshgrid(x,y)
plt.scatter(X,Y)
plt.savefig("格子状の点.png")
plt.show()
これに、高さの情報が加わると三次元情報を内包するコンター図や等高線図を描写することができるようになる。
点電荷の電場と電位の描写
電位分布の描写
試しに、正の電荷をおいたときのその周りに生じる電位分布を描くプログラムを以下のようにして作成することを考える。
ただし、点電荷における電位は二次元空間内だと以下のように表すことができる。
V(r) = k\frac{Q}{r}
$r$は、点電荷からの距離で$Q$は電荷で$k$はクーロン定数である。
したがって、これをxy座標系で表すと以下のようになる。
V(x,y) = k\frac{Q}{\sqrt{x^2+y^2}}
contourf(x,y,z)を用いた描写
これをもとにして以下のようなプログラムを作成する。
import matplotlib.pyplot as plt
import math
import numpy as np
import japanize_matplotlib
n=10
x=np.linspace(-1,1,n)
y=np.linspace(-1,1,n)
X,Y = np.meshgrid(x,y)
R=(X**2+Y**2)**0.5
Q=1
k=9.0*10**9
V= k*Q/R
plt.contourf(X,Y,V)
plt.colorbar()
plt.savefig("点電荷の電位分布.png")
plt.show()
電場分布の描写
一方で、電場ベクトルは、
\textbf{E}=-\frac{dV}{dr}
より、
\textbf{E}=\frac{kQ}{r^2}\frac{\textbf{r}}{r}
したがって、xy直交座標系では、電場は以下のように表すことができる。
E_x = \frac{kQ}{\sqrt{x^2+y^2}^3}x,E_y=\frac{kQ}{\sqrt{x^2+y^2}^3}y
quiver(x,y,u,v)での描写
これをquiver(x,y,u,v)を用いて、矢印一本ずつ描写すると以下のようになる。
import matplotlib.pyplot as plt
import math
import numpy as np
import japanize_matplotlib
n=10
x=np.linspace(-1,1,n)
y=np.linspace(-1,1,n)
X,Y = np.meshgrid(x,y)
R=(X**2+Y**2)**0.5
Q=1
k=9.0*10**9
E= k*Q/R**2
Ex=E*X/R
Ey=E*Y/R
plt.quiver(X,Y,Ex,Ey)
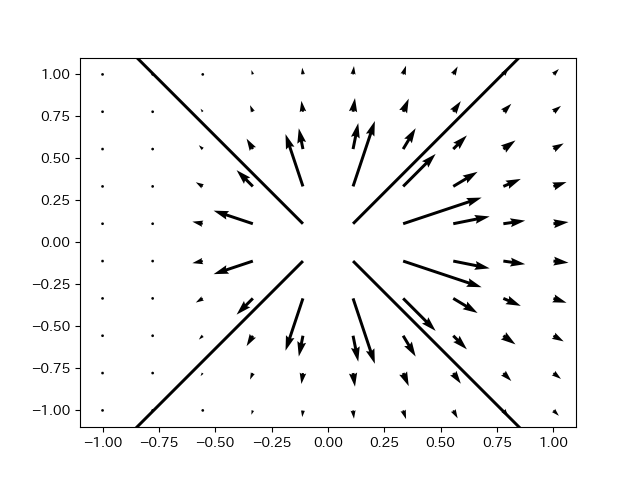
plt.savefig("点電荷の電場分布.png")
plt.show()
これを実行すると以下のような画像が出力される。

この画像から分かるように$r=0$付近で矢印の大きさが発散してしまうことが分かる。また、ベクトル場描写もあまり見やすいとは言えない。
streamplot(x,y,u,v)での描写
一方で、streamplot(x,y,u,v)で描写すると以下のようになる。ただし、streamplot(x,y,u,v)では、x,yが直交座標系でないとエラーがでてしまい上手く描写することができないので注意すること。
import matplotlib.pyplot as plt
import math
import numpy as np
import japanize_matplotlib
n=10
x=np.linspace(-1,1,n)
y=np.linspace(-1,1,n)
X,Y = np.meshgrid(x,y)
R=(X**2+Y**2)**0.5
Q=1
k=9.0*10**9
E= k*Q/R**2
Ex=E*X/R
Ey=E*Y/R
plt.streamplot(X,Y,Ex,Ey)
plt.savefig("点電荷の電場分布_流れ.png")
plt.show()
streamplot(x,y,u,v)では、quiver(x,y,u,v)よりも描写できる制限が厳しい一方で、このように上手く流れの場を表現することができる。このような流れの場を表現することができるので、以下のようなソレノイドコイルに生じる磁場の流れも表現することが可能になる。
本題から外れるが、ソレノイドのプログラムが欲しい方は、以下のリンクを辿って欲しい。
微分操作の演算
先ほどの計算は、電場は電位の微分にマイナスを付けたものだという定義を人間が計算してその結果を用いたとも言える。しかし、実際の演算ではそのようにいかない複雑な場合も多い。そこで、微分の演算もコンピュータに行ってもらおう。
微分の原理を用いてライブラリに依存せず考察した場合とライブラリ(numpy.gradient)を用いた場合について考える。
ライブラリなし
まずは、微分操作をコーディングで表すことができるかを考える。
\frac{\Delta y}{\Delta x}= \frac{y(x+h)-y(x)}{(x+h)-x}= \frac{y(x+h)-y(x)}{h}
という微分の定義を上手く活用する。ただし$h$は微小変化分である。
import matplotlib.pyplot as plt
import math
import numpy as np
import japanize_matplotlib
n=10
x=np.linspace(-1,1,n)
y=np.linspace(-1,1,n)
X,Y = np.meshgrid(x,y)
#R=(X**2+Y**2)**0.5
Q=1
k=9.0*10**9
#V=k*Q/R
# 電位関数定義
def deni(x,y):
r=(x**2+y**2)**0.5
v=k*Q/r
return v
#微分操作
## 変数宣言
diff_x=np.zeros((n,n))
diff_y=np.zeros((n,n))
## 微小変化分
h=1.0*10**(-6)
for i in range(n):
for k in range(n):
diff_x[i][k]=(deni(X[i][k]+h,Y[i][k])-deni(X[i][k],Y[i][k]))/h
diff_y[i][k]=(deni(X[i][k],Y[i][k]+h)-deni(X[i][k],Y[i][k]))/h
##電場の符号合わせ
Ex=-diff_x
Ey=-diff_y
plt.quiver(X,Y,Ex,Ey)
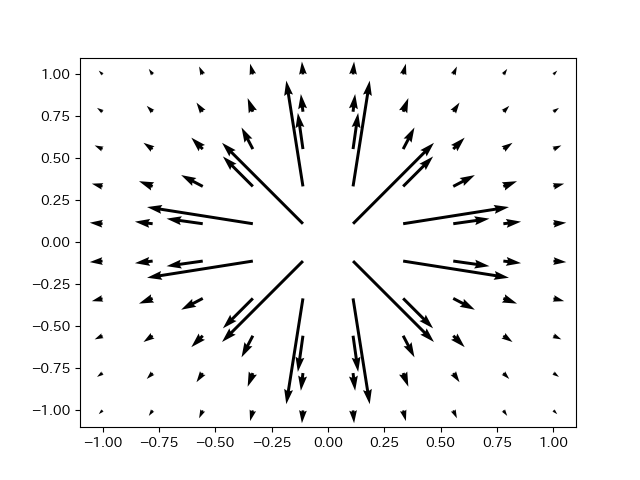
plt.savefig("点電荷の電場分布_微分の定義使用.png")
plt.show()
このプログラムを実行すると以下のようになる。
このように、上手く微分を表すことができているようである。
ライブラリありの場合
次に、numpy.gradientという便利なライブラリを用いた例についても考察する。
ちなみに計算方法は以下のような式を基礎として作られている。
\frac{\Delta y}{\Delta x}= \frac{y(x+h)-y(x-h)}{(x+h)-(x-h)}= \frac{y(x+h)-y(x-h)}{2h}
以下のようなプログラムを書く。
import matplotlib.pyplot as plt
import math
import numpy as np
import japanize_matplotlib
n=10
x=np.linspace(-1,1,n)
y=np.linspace(-1,1,n)
X,Y = np.meshgrid(x,y)
R=(X**2+Y**2)**0.5
Q=1
k=9.0*10**9
V= k*Q/R
#y,xの順番で書かないとgradientは上手く機能しないので気をつける!!
dVdY,dVdX=np.gradient(V,y,x)
Ex=-dVdX
Ey=-dVdY
plt.quiver(X,Y,Ex,Ey)
plt.savefig("点電荷の電場分布_gradient使用.png")
plt.show()
この場合、上手くライブラリが機能しているので微分機能がしっかりと働いているということが分かる。
まとめ
今回は、点電荷によって生じる電場の分布をPythonで描写することにより、ベクトル場、流れの場の描写方法を学んだ。一般的に、quiver(x,y,u,v)の方が、streamplot(x,y,u,v)よりも描写方法が簡単ではあるが、複雑な流れの情報を知るためには、streamplot(x,y,u,v)を用いた方が良いと考えられる。