はじめに
高校数学2、3において放物線、円、楕円、双曲線の軌跡と方程式は頻出である。しかし、定義からそれらを実際に図示してみるという取り組みはあまりないようである。従って、本記事ではPythonを用いて、定義からそれぞれのグラフを描写することができるかどうかを考察する。具体的には、まず各曲線において描き方(定義)を述べ、それに応じたプログラムを作ることでどのようなグラフになるのかを図示する。
円
定義
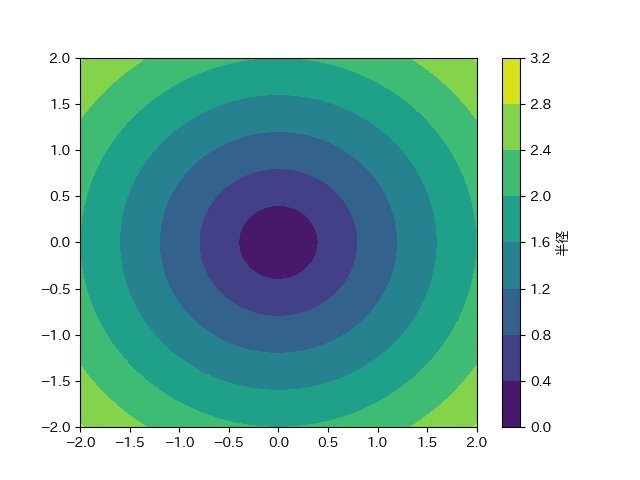
定点から距離が一定の点が描く軌跡を円と呼ぶ。
プログラム
複素数平面を用いてプログラムを作成した。
python circle_tra.py
import numpy as np
import matplotlib.pyplot as plt
import math
import japanize_matplotlib
m=2
n=100
#座標空間の設定
x=np.linspace(-m,m,n)
y=np.linspace(-m,m,n)
X,Y=np.meshgrid(x,y)
#Z=(X**2+Y**2)**0.5
Z=abs(X+1j*Y)
plt.contourf(X,Y,Z)
plt.colorbar(label="半径")
plt.savefig("円の軌跡.png")
plt.show()
楕円
定義
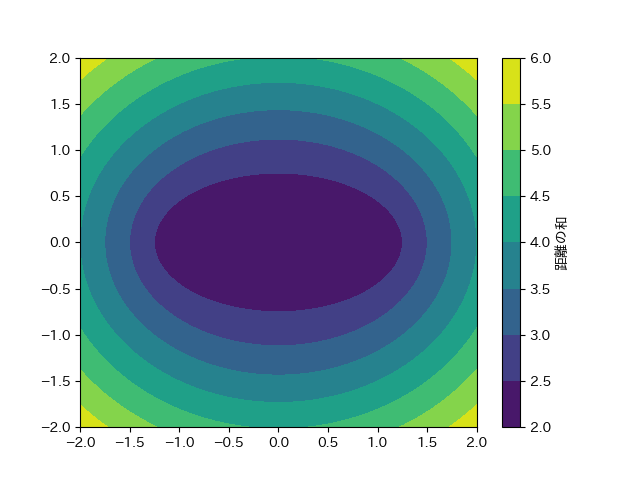
2点からの距離の和が一定な点が描く軌跡のことを楕円と呼ぶ。
プログラム
ell_tra.py
import numpy as np
import matplotlib.pyplot as plt
import math
import japanize_matplotlib
m=2
n=100
#座標空間の設定
x=np.linspace(-m,m,n)
y=np.linspace(-m,m,n)
X,Y=np.meshgrid(x,y)
Z_a=1
Z_b=-1
z=X+1j*Y
Z=abs(z-Z_a)+abs(z-Z_b)
plt.contourf(X,Y,Z)
plt.colorbar(label="距離の和")
plt.savefig("楕円の軌跡.png")
plt.show()
双曲線
定義
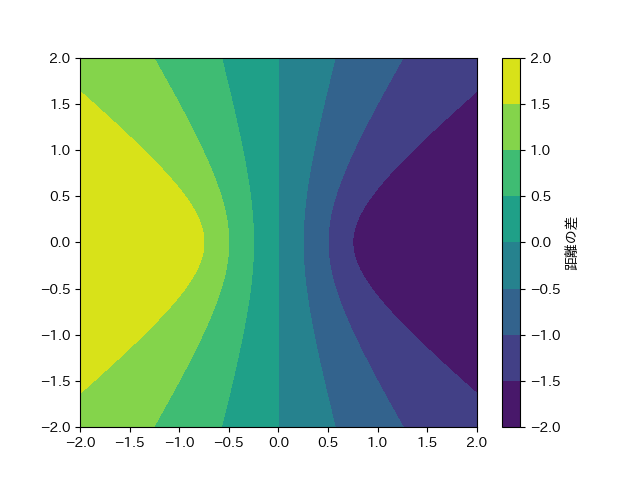
2点間からの距離の差が一定になるような点が描く軌跡を双曲線と呼ぶ。
プログラム
python hyper_tra.py
import numpy as np
import matplotlib.pyplot as plt
import math
import japanize_matplotlib
m=2
n=100
#座標空間の設定
x=np.linspace(-m,m,n)
y=np.linspace(-m,m,n)
X,Y=np.meshgrid(x,y)
Z_a=1
Z_b=-1
z=X+1j*Y
Z=abs(z-Z_a)-abs(z-Z_b)
plt.contourf(X,Y,Z)
plt.colorbar(label="距離の差")
plt.savefig("双曲線の軌跡.png")
plt.show()
放物線
定義
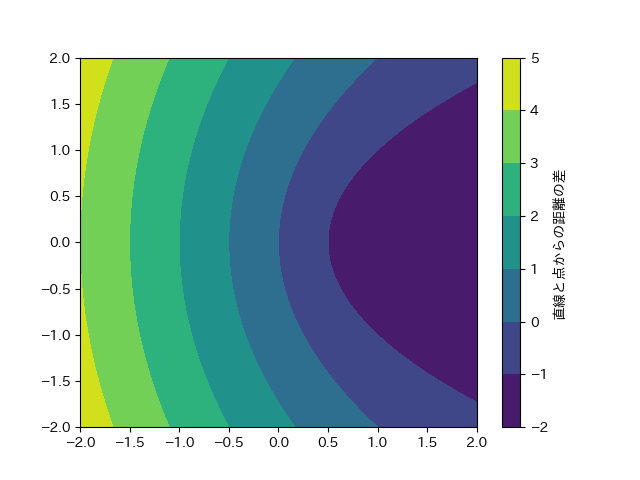
ある点とある直線からの距離が等しくなるような点が描く軌跡を放物線と呼ぶ。
プログラム
python par_tra.py
import numpy as np
import matplotlib.pyplot as plt
import math
import japanize_matplotlib
m=2
n=100
#座標空間の設定
x=np.linspace(-m,m,n)
y=np.linspace(-m,m,n)
X,Y=np.meshgrid(x,y)
Z_x=-1
Z=1
z=X+1j*Y
Z=abs(z-Z)-(z-Z_x).real
plt.contourf(X,Y,Z)
plt.colorbar(label="直線と点からの距離の差")
plt.savefig("放物線.png")
plt.show()
まとめ
今回は、コンター図を用いて二次曲線の軌跡を定義からプログラムを用いて描写した。ただし、描写においては複素数平面を用いた。結果としてきれいに描写することができていることが分かった。