はじめに
潮流計算とは、あらかじめ系統の発電機の出力や負荷の消費電力が与えられた場合において、送電線にかかる電圧や潮流を逆解析を用いて推定する方法である。逆解析の方法については、非線形問題でも扱うことができるニュートンラフソン法などが用いられる。ニュートンラフソン法では、曲面の傾きにあたるヤコビアンを偏微分により算出して、最適解を近似する。本記事では、非線形問題である電力方程式をヤコビアン行列を用いた式に変形し、ニュートンラフソン法で解くことを目的とする。ただし、本記事で説明したモデルは、『令和3年度の電験一種二次試験、電力管理における第3問』である。
以下簡単に本記事で行った解析結果の概要を述べる。
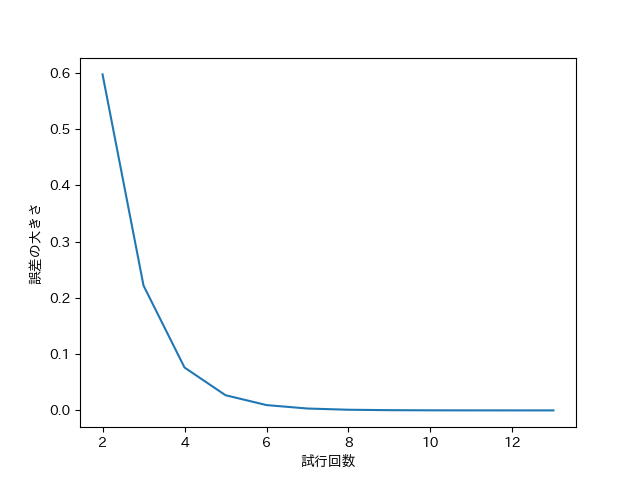
まず、以下の画像は解析結果であり、計算の収束状況を表している。意外なことに、シンプルなアルゴリズムながら数回のステップで、かなり収束する。
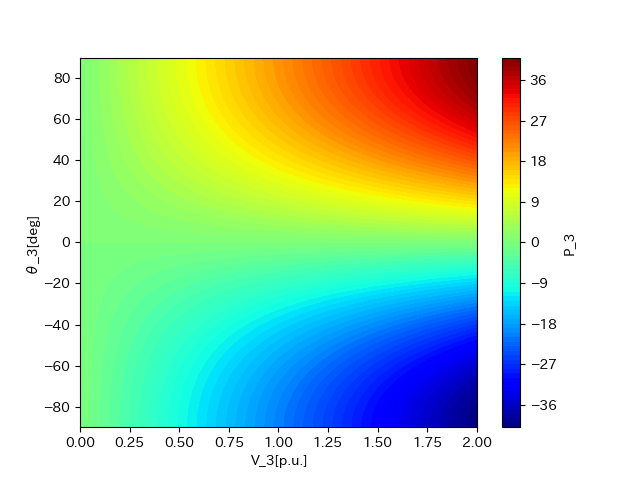
一方で、電圧の情報(大きさと位相角)とそれが影響を与える有効電力の関係を以下のグラフ示す。このグラフは符号の変化がないような微小な変化幅ではほぼ単峰性を示す。したがってニュートンラフソン法を用いて電力方程式を解析するのは、有効な方法といえる。(局所解が存在しにくいため)
問題設定
令和3年度の電験一種二次試験、電力管理における第3問の問題をモデルとする。
問題の難易度など詳しい情報については、電験王様を参照にされたい。
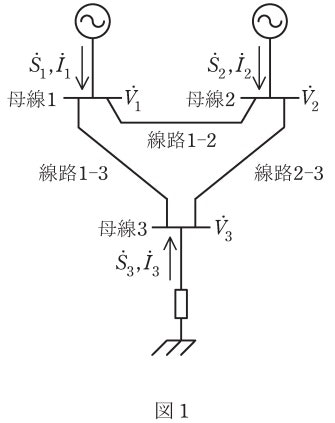
電力系統図は以下のとおりとする。
ノードアドミタンスは、以下の通りとする。
\dot{Y}=
\begin{pmatrix}
-18j & j10 & j10\\
j10 & -18j & j10\\
j10 & j10 & -18j\\
\end{pmatrix}
みてのとおり、今回は送電線の抵抗値は無視し、インダクタンスと静電容量のみを考慮する。
これにより、電流の式は以下のようになる。
\begin{pmatrix}
\dot{I_1} \\
\dot{I_2} \\
\dot{I_3} \\
\end{pmatrix}
= \dot{Y}
\begin{pmatrix}
\dot{V_1} \\
\dot{V_2} \\
\dot{V_3} \\
\end{pmatrix}
これにより、各ノードの皮相電力は以下のように表すことができる。ただし、遅れを正とする。
\begin{pmatrix}
\dot{S_1} \\
\dot{S_2} \\
\dot{S_3} \\
\end{pmatrix}
=
\begin{pmatrix}
\dot{V_1} \\
\dot{V_2} \\
\dot{V_3} \\
\end{pmatrix}
\begin{pmatrix}
\bar{I_1} \\
\bar{I_2} \\
\bar{I_3} \\
\end{pmatrix}
ただし、系統の電圧を以下のように表すとする。
\begin{pmatrix}
\dot{V_1} \\
\dot{V_2} \\
\dot{V_3} \\
\end{pmatrix}
=
\begin{pmatrix}
V_1(cos\theta_1+jsin\theta_1) \\
V_2(cos\theta_2+jsin\theta_2)\\
V_3(cos\theta_3+jsin\theta_3) \\
\end{pmatrix}
=
\begin{pmatrix}
V_1e^{j\theta_1} \\
V_2e^{j\theta_2} \\
V_3e^{j\theta_3} \\
\end{pmatrix}
ゆえに、系統電圧が決定されると陽的に各ノードの皮相電力が決定される。したがって、逆解析であるニュートンラフソン法を用いることで系統の電力さえ分かれば、系統電圧を推定することができる。
ニュートンラフソン法
ニュートンラフソン法は、非線形の方程式に対して各区間を擬似的に線形に直して最適値を簡易的に推定するアルゴリズムである。
これは、電力方程式の問題を非線形曲面の最適化問題と捉えることで解析する。その際に用いるのが曲面の傾きに相当する行列ヤコビアンである。
本記事では、上のフロチャートに対して以下のような設定をすることでアルゴリズムを組み立てる。
\boldsymbol{y_e}=
\begin{pmatrix}
P_{2e} \\
P_{3e} \\
Q_{3e} \\
\end{pmatrix}
,\boldsymbol{x_e}=
\begin{pmatrix}
\theta_{2e} \\
\theta_{3e} \\
|\dot{V_3}|_e \\
\end{pmatrix}
ただし、本記事では、前提として最適化する電力方程式の曲面を単峰性と仮定している。つまり、局部が存在しないということを前提にニュートンラフソン法を採用している。したがって、後半の記事では電力方程式の解空間を描写することで単峰性であることを検証している。
アルゴリズム
系統電圧(原因)が変化すると電力(結果)が変化する。
したがって、結果の物性量が変化すればそれに応じてほぼ線形的に原因の物性量が変化するはずである(仮定)。
\boldsymbol{\Delta f}=\boldsymbol{J(x_e)}\boldsymbol{\Delta x}
ただし、$\boldsymbol{J}$はヤコビアン行列であり、
\boldsymbol{\Delta f}=
\begin{pmatrix}
\Delta{P_2} \\
\Delta{P_3} \\
\Delta{Q_3} \\
\end{pmatrix}
,
\boldsymbol{\Delta x}=
\begin{pmatrix}
\Delta{\theta_2} \\
\Delta{\theta_3} \\
\Delta{|\dot{V_3}|} \\
\end{pmatrix}
ゆえに、
\begin{pmatrix}
\Delta{P_2} \\
\Delta{P_3} \\
\Delta{Q_3} \\
\end{pmatrix}
=
\boldsymbol{J}
\begin{pmatrix}
\Delta{\theta_2} \\
\Delta{\theta_3} \\
\Delta{|\dot{V_3}|} \\
\end{pmatrix}
が成立する。(原因→結果の式)
ここで、電力方程式を以下のようなヤコビアン行列を用いた式に変形する。
\boldsymbol{\Delta x}=\boldsymbol{J^{-1}(x_e)}\boldsymbol{\Delta f}
つまり、
\begin{pmatrix}
\Delta{\theta_2} \\
\Delta{\theta_3} \\
\Delta{|\dot{V_3}|} \\
\end{pmatrix}
=
\boldsymbol{J^{-1}}
\begin{pmatrix}
\Delta{P_2} \\
\Delta{P_3} \\
\Delta{Q_3} \\
\end{pmatrix}
ただし、右辺は実際の電力と推定された電力の差である。
上記の左辺を初期状態の電圧値$\boldsymbol{x_e}$に以下の式のように$\Delta \boldsymbol{x}$加算することを繰り返すことによって最適化を行う。
\boldsymbol{x_e} = \boldsymbol{x_e}+\boldsymbol{\Delta x}
ただし、
\boldsymbol{J}=
\begin{pmatrix}
\frac{\delta P_2}{\delta \theta_2} & \frac{\delta P_2}{\delta \theta_3} & \frac{\delta P_2}{\delta |\dot{V_3}|}\\
\frac{\delta P_3}{\delta \theta_2} & \frac{\delta P_3}{\delta \theta_3} & \frac{\delta P_3}{\delta |\dot{V_3}|}\\
\frac{\delta Q_2}{\delta \theta_2} & \frac{\delta Q_2}{\delta \theta_3} & \frac{\delta Q_2}{\delta |\dot{V_3}|}
\end{pmatrix}
とし、偏微分は以下の例のような差分法で近似するものとする。
例
\frac{\delta P_2}{\delta \theta_2} = \frac{P_2(\theta_2+\Delta)-P_2(\theta_2)}{(\theta_2+\Delta)-\theta_2}=\frac{ P_2(\theta_2+\Delta)-P_2(\theta_2)}{\Delta}
ただし、$\Delta$は共通な微小量とする。(本記事では、0.01程度としたが、$1.0\times 10^{-5}$程度でも結果はほぼ同じとなった。)
プログラム
前提条件と収束条件
前提条件として以下のような設定を考える。
目標値は以下の通りとする。
\boldsymbol{y_s} =
\begin{pmatrix}
0.7 \\
1.0 \\
0.3 \\
\end{pmatrix}
系統電圧の初期条件は以下の通りとする。
V_1=1,V_2=1.05,V_3=1,\theta_1=\theta_2=\theta_3=0
したがって、
\boldsymbol{x^0_e}=
\begin{pmatrix}
\theta^0_{2e} \\
\theta^0_{3e} \\
|\dot{V_3}|^0_e \\
\end{pmatrix}
=
\begin{pmatrix}
0 \\
0 \\
1 \\
\end{pmatrix}
となる。
また、収束条件は以下のとおりである。
|\boldsymbol{\Delta f}|<1.0\times 10^{-5}
ただし、
\boldsymbol{\Delta f}=\boldsymbol{y_s}-\boldsymbol{y(x_e)}
とする。
ここで、この条件でPythonを用いてプログラムを書くと以下のとおりである。
Pythonプログラム
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
# 偏微分を行うために必要な微小変化
delta=0.01
# 試行回数
i=1
# 誤差と試行回数のデータを保存するための配列
num=[]
error=[]
#ノードアドミタンス行列の定義
a=-18j
b=10j
Y_dot=np.array([[a, b, b], [b, a, b],[b, b, a]])
# 目標となる応答値(電力)
y_s_dot = np.array([0.7, 1.0, 0.3])
#電圧の定義(初期条件)
V_1=1
theta_1=0
V_2=1.05
theta_2=0
# 問題にはなかったが新規追加した変数
V_3=1
theta_3=0
V_1_dot=V_1*np.exp(1j*theta_1)
# 電力方程式:電圧から電力を推定する。
def denrixoku_houteisiki(theta_2, theta_3, V_3):
#x_e_dot =np.array([theta_2, theta_3, V_3])
V_2_dot=V_2*np.exp(1j*theta_2)
V_3_dot=V_3*np.exp(1j*theta_3)
V_dot = np.array([V_1_dot, V_2_dot, V_3_dot])
I_dot= Y_dot @ V_dot
S_dot = V_dot * np.conjugate(I_dot)
y_e_dot = np.array([S_dot[1].real, S_dot[2].real, S_dot[2].imag])
return y_e_dot
x_e_dot =np.array([theta_2, theta_3, V_3])
y_e_dot = denrixoku_houteisiki(x_e_dot[0], x_e_dot[1], x_e_dot[2])
delta_f = y_s_dot-y_e_dot
# デルタfの大きさが一定の値より小さくなるまで繰り返す
while (delta_f[0]**2+delta_f[1]**2+delta_f[2]**2)**0.5 > 10**(-5):
#ヤコビアンの計算(偏微分の近似をする)
S_2_theta_2 = (denrixoku_houteisiki(theta_2+delta,theta_3,V_3)-denrixoku_houteisiki(theta_2,theta_3,V_3))/delta
S_2_theta_3 = (denrixoku_houteisiki(theta_2,theta_3+delta,V_3)-denrixoku_houteisiki(theta_2,theta_3,V_3))/delta
S_2_v_3 = (denrixoku_houteisiki(theta_2,theta_3,V_3+delta)-denrixoku_houteisiki(theta_2,theta_3,V_3))/delta
J_dot = np.array([[S_2_theta_2[0], S_2_theta_3[0], S_2_v_3[0]], [S_2_theta_2[1], S_2_theta_3[1], S_2_v_3[1]], [S_2_theta_2[2], S_2_theta_3[2], S_2_v_3[2]]])
# デルタx_dotの計算
delta_x_dot = np.linalg.pinv(J_dot) @ delta_f
# x_dotの更新
x_e_dot = x_e_dot + delta_x_dot
# y_dotの更新
y_e_dot = denrixoku_houteisiki(x_e_dot[0], x_e_dot[1], x_e_dot[2])
# 誤差の更新
delta_f = y_s_dot-y_e_dot
i=i+1
num.append(i)
error.append((delta_f[0]**2+delta_f[1]**2+delta_f[2]**2)**0.5)
plt.plot(num, error)
plt.xlabel('試行回数')
plt.ylabel('誤差の大きさ')
plt.savefig('潮流解析.png')
plt.show()
# 結果の出力
print(x_e_dot)
y_e_dot = denrixoku_houteisiki(x_e_dot[0], x_e_dot[1], x_e_dot[2])
print(y_e_dot)
このプログラムを実行すると以下のようなファイルが出力される。
このように、数回のステップで、かなり誤差が軽減されているということが分かる。特に、1,2回目のステップを回しただけで誤差が約10分の1になるのは驚きである。というのは、シンプルなアルゴリズムより、個人的にはもう少し計算時間がかかると踏んでいたからである。
一方で、出力されるログの結果は以下のようになる。ただし、以下のことに注意する。
\boldsymbol{y_e}=
\begin{pmatrix}
P_{2e} \\
P_{3e} \\
Q_{3e} \\
\end{pmatrix}
,\boldsymbol{x_e}=
\begin{pmatrix}
\theta_{2e} \\
\theta_{3e} \\
|\dot{V_3}|_e \\
\end{pmatrix}
[0.07399652 0.08030305 1.15155981]
[0.70000037 0.99999835 0.29999395]
前半のベクトル配列が$\boldsymbol{x_e}$で、後半のベクトル配列が、$\boldsymbol{y_e}$である。ここで、目標値は、
\boldsymbol{y_s} =
\begin{pmatrix}
0.7 \\
1.0 \\
0.3 \\
\end{pmatrix}
であることから、計算推定値はかなり目標値に漸近していると言える。
電力方程式の解空間
ニュートンラフソン法では、単峰性つまり山が一つの場合しか適正な探索ができないという性質がある。(最適値ではなく、極値に落ち着く可能性があるため)
したがって、電力方程式の原因である系統電圧と結果である電力に対して、単峰性の関係性があることが望ましい。
そこで、電力方程式の電圧条件、今回は$V_3,\theta_3$が変化した場合、$P_3$がどのように変化するのかを調べたい。他のパラメータは固定として考えるので、以下のようなプログラムを書いた。
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import math
#ノードアドミタンス行列の定義
a=-18j
b=10j
Y_dot=np.array([[a, b, b], [b, a, b],[b, b, a]])
#電圧の定義(初期条件)
V_1=1
theta_1=0
V_2=1.05
theta_2=0
# 問題にはなかったが新規追加した変数
n=100
V_3=np.linspace(0,2,n)
theta_3=np.linspace(-math.pi/2,math.pi/2,n)
V_3, theta_3 = np.meshgrid(V_3, theta_3)
P_3=np.zeros((n,n))
for i in range(n):
for k in range(n):
V_3_s = V_3[i][k]
theta_3_s = theta_3[i][k]
V_1_dot=V_1*np.exp(1j*theta_1)
V_2_dot=V_2*np.exp(1j*theta_2)
V_3_dot=V_3_s*np.exp(1j*theta_3_s)
V_dot = np.array([V_1_dot, V_2_dot, V_3_dot])
I_dot= Y_dot @ V_dot
S_dot = V_dot * np.conjugate(I_dot)
P_dot = np.real(S_dot)
P_3[i][k]=P_dot[2]
plt.contourf(V_3, theta_3*(180/math.pi), P_3, levels=100, cmap='jet')
plt.xlabel('V_3[p.u.]')
plt.ylabel('θ_3[deg]')
plt.colorbar(label='P_3')
plt.savefig('denken_3d.png')
plt.show()
このグラフより分かることは、系統電圧や位相角(力率角ではないので注意する)が少しだけ変化したなとしても、有効電力の符号は変化せず単峰性であるとみなすことができることである。したがって、ニュートンラフソン法による潮流計算は有効であると考えられる。
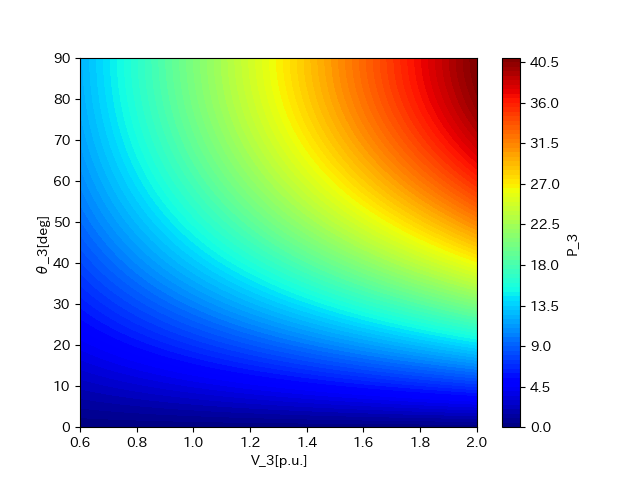
そこで、通常の遅れ運転に近い条件である、
$0.6[p.u.]<V_3<2.0[p.u.],0<\theta_3<\frac{\pi}{2}$の範囲に限定してプロットすると以下のグラフのようになる。
このグラフから分かる通り電圧が大きく位相角の符号や大きさが変化しにくい平常時の運転の場合、単峰性を示すことから、ニュートンラフソン法が有効であるということが再確認できる。
まとめ
今回は、電験の過去問を用いて潮流計算を行った。本問では、比較的すくないステップ数でかなり精度の良い値を得ることができた。ただし、系統のノード数が増えるとヤコビアンが2乗のオーダで大きくなる。ゆえに、計算量が爆増すると考えられる。そこで、複雑な系統のシミュレーションではアルゴリズムを工夫したり、粗い近似解を得られる直流法を採用するといった方法が有効である。また、後半では電力方程式の電圧と電力の関係を調査した。具体的には、3次元の等高線図にして観察を行ったところ、等高線図の概形は単峰性を示すものとなった。したがって、ニュートンラフソン法を用いる際の心配事である解の局部探査は考慮しなくて済む。これにより、潮流計算においてニュートンラフソン法は計算量や精度の観点から妥当であると言える。このように、電力工学の範囲でもコンピュータサイエンスの知識が役立つ場合があるので、しっかりと勉強しておくと良いかもしれない。
参考文献