はじめに
近年の電力系統は、発電所から需要家に電力を送る一方向モデルから再エネ設備による発電なども合わせた双方向的なモデルとなり複雑さを増している。したがって、そのような系統を数学的に解析するのは、手計算ではほぼ不可能である。そこで、計算機を用いたシミュレーションを行う必要性がでてくる。
今回は、最も単純な系統モデル（同期発電機-送電線-静止負荷）の過渡解析をPythonを用いて行うことで、系統の解析に必要な知識を復習することを目的とする。
以下、計算結果の概要を述べる。
同期発電機にガバナ特性（周波数変動に対して比例的な負のフィードバック制御を発電機の機械的入力にかける特性）を持たせ、有効電力と周波数の過渡的な応答を調べた。
結果、系統周波数が上昇した場合、発電機の機械的入力を減らすことで系統を安定化することができた。
※今回は生成AIであるChatGPTをプログラムの推敲手段として使用した。
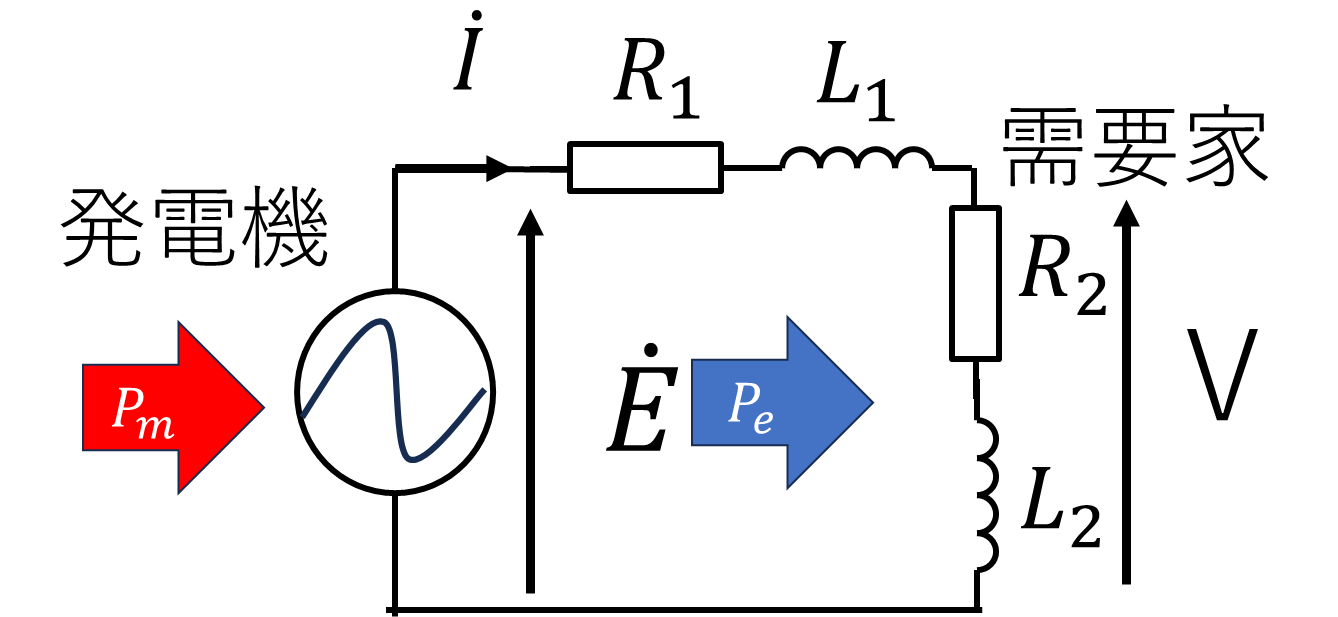
系統モデル
以下のような、最も単純な系統モデル（同期発電機-送電線-静止負荷）を考える。
だだし静止負荷は、RL直列回路であり、送電線はRL分のみから成るとする。
また、発電機の容量等に実際のデータを入れるのは難しいため、そのような要素は単位法を用いた。したがって、代表相のみを今回は扱う。
解析方法
方法としては、至ってシンプルで、発電機の動揺方程式（力学的な方程式）と系統の電力方程式（複素数を用いた電気的な方程式）を連立させる。
発電機の動揺方程式
単位法換算での動揺方程式は以下のように表すことができる。
2H \frac{d\omega }{dt}+D\omega=P_m-P_e
ただし、$H$は慣性定数[s],$D$はダンピングトルク係数(今回は使用しないので0とした。),$P_e$は電気的出力[pu],$P_m$は発電機の機械的入力[pu],$\omega$は系統角速度[pu]とした。
電気的な方程式
一方で、電気的な関係式は以下のようになる。
まず、$V$を位相の基準とした電圧の式をキルヒホッフの第2法則より示す。
\dot{E}=E\exp{(j\delta)}
ただし、上式を用いる場合は$\delta$[rad]でなければいけないことに注意する。
\dot{E}=V+(R_1+j \omega L_1)\dot{I}
V=(R_2+j \omega L_2)\dot{I}
ただし、$\delta$[pu]は起電力と系統電圧の位相差であり、以下のように表される。
\delta(t) =\int_{0}^{t} \omega (t)dt
一方で、上記の関係を元に、電力方程式を構築すると以下のようになる。
\dot{S_e}=P_e+jQ_e=E\bar{I}
制御方法
また、発電機側の制御方法として、以下のような簡易なガバナフリー制御を設けた。
\Delta P_m = -\alpha \Delta f
ただし、$\alpha$はガバナフリー制御に対する定数とする。これは、$P_m$の変化分に対して$f$の変化分の比例制御をかけているということである。
計算方法
上記の連立された微分方程式を解くのは、手計算では不可能に近いので、計算機を用いて近似解を算出する。その方法の1つに数値計算が挙げられる。今回は、かなり複雑な計算になりそうなので、いつも用いている1次のオイラー法ではなく4次のルンゲクッタ法を用いる。(ルンゲクッタ法の実装に生成AIを用いた。)
プログラム
以下のようなプログラムを作成した。
import numpy as np
import math
import cmath
import matplotlib.pyplot as plt
import japanize_matplotlib
# =========================
# Base / constants
# =========================
f0 = 50.0 # [Hz]
omega_b = 2.0 * math.pi * f0 # [rad/s]
# =========================
# Generator & swing params (pu)
# =========================
H = 4.0 # [s] inertia constant
D = 0.0 # [-] damping (pu torque per pu speed)
E_mag = 1.10 # |E| (pu)
# =========================
# Network: series Z1 (line etc.) + RL load Z2
# 入力は「ベース周波数時のリアクタンス」
# =========================
#送電線のパラメータ
R1 = 0.10 # pu
X1_base = 0.60 # pu @ f0 ← L1相当は X1_base にまとめる
#負荷側（需要家側）のパラメータ
R2 = 1.00 # pu
X2_base = 1.00 # pu @ f0 ← L2相当は X2_base にまとめる
# 周波数偏差 Δω に応じたリアクタンス補正（一次近似）
def reactances(dw_pu: float):
X1 = X1_base * (1.0 + dw_pu) # X ∝ ω
X2 = X2_base * (1.0 + dw_pu)
return X1, X2
# =========================
# Electrical calculations
# =========================
def currents_and_voltages(delta: float, dw: float):
"""
E∠δ ---- Z1=R1+jX1 ---- Z2=R2+jX2 (RL load)
I = E∠δ / (Z1 + Z2)
V_load = I * Z2
"""
X1, X2 = reactances(dw)
Z1 = complex(R1, X1)
Z2 = complex(R2, X2)
Z_tot = Z1 + Z2
E = cmath.rect(E_mag, delta) # E∠δ
I = E / Z_tot
V_load = I * Z2
return E, I, V_load
def electrical_power(delta: float, dw: float) -> float:
"""
発電機端の実電力 P_e = Re{ E * conj(I) } を返す（pu）。
"""
E, I, _ = currents_and_voltages(delta, dw)
S_gen = E * np.conj(I)
return float(S_gen.real)
# =========================
# Swing ODE (pu-unified)
# state = [delta(rad), dw(pu)]
# =========================
def rhs(state, t,P_m):
delta, dw = state
P_e = electrical_power(delta, dw)
ddelta_dt = omega_b * dw
ddw_dt = (P_m - P_e - D * dw) / (2.0 * H)
return np.array([ddelta_dt, ddw_dt], dtype=float), P_e
def rk4_step(state, t, dt,P_m ):
k1, _ = rhs(state, t, P_m)
k2, _ = rhs(state + 0.5*dt*k1, t + 0.5*dt,P_m)
k3, _ = rhs(state + 0.5*dt*k2, t + 0.5*dt, P_m)
k4, _ = rhs(state + dt*k3, t + dt, P_m )
return state + (dt/6.0)*(k1 + 2*k2 + 2*k3 + k4)
# =========================
# Simulation setup
# =========================
t = 0.0
t_end = 5 # [s]
dt = 1.0e-4 # RK4 step
# 初期状態: 角度0, 速度偏差0
state = np.array([0.0, 0.0], dtype=float)
P_m = 1.00 # mechanical initial input (pu)
alpha=100 # governor-free operation P-control parameter
ts, fHz, del_deg, Vmag, Vang_deg, Pe_log, Pm_log, I_mag = [], [], [], [], [], [], [], []
# =========================
# Time stepping
# =========================
while t <= t_end + 1e-12:
delta, dw = state
# ログ（現在の電気量）
E, I, V_load = currents_and_voltages(delta, dw)
P_e = electrical_power(delta, dw)
f_now = f0 * (1.0 + dw) # [Hz]
ts.append(t)
fHz.append(f_now)
del_deg.append(delta * 180.0 / math.pi)
Vmag.append(abs(V_load))
Vang_deg.append(cmath.phase(V_load) * 180.0 / math.pi)
Pe_log.append(P_e)
Pm_log.append(P_m)
I_mag.append(abs(I))
k_ary=rhs(state, t,P_m)[0]
# governor-free operation P-control parameter
P_m=P_m-alpha*dt*k_ary[1]
# 次ステップ（RK4）
state = rk4_step(state, t, dt,P_m )
t += dt
# =========================
# Plots
# =========================
#周波数解析
plt.figure(); plt.plot(ts, fHz); plt.xlabel("t [s]"); plt.ylabel("f [Hz]")
plt.title("System Frequency (pu swing with RL load)"); plt.grid(True); plt.tight_layout()
plt.savefig("freq.png", dpi=150); plt.show()
#電圧位相角解析
plt.figure(); plt.plot(ts, del_deg); plt.xlabel("t [s]"); plt.ylabel("delta [deg]")
plt.title("Rotor Angle"); plt.grid(True); plt.tight_layout()
plt.savefig("delta_deg.png", dpi=150); plt.show()
#需要家電圧の大きさ解析
plt.figure(); plt.plot(ts, Vmag); plt.xlabel("t [s]"); plt.ylabel("|V_load| [pu]")
plt.title("Load Voltage Magnitude"); plt.grid(True); plt.tight_layout()
plt.savefig("V_load_mag.png", dpi=150); plt.show()
#需要家電圧の位相解析（常に0となるはず。確認用もしくは不要）
plt.figure(); plt.plot(ts, Vang_deg); plt.xlabel("t [s]"); plt.ylabel("∠V_load [deg]")
plt.title("Load Voltage Angle"); plt.grid(True); plt.tight_layout()
plt.savefig("V_load_ang.png", dpi=150); plt.show()
#発電機電気的出力解析
plt.figure(); plt.plot(ts, Pe_log, label="P_e"); plt.plot(ts, Pm_log, label="P_m")
plt.xlabel("t [s]"); plt.ylabel("Power [pu]"); plt.legend()
plt.title("Electrical vs Mechanical Power (at generator terminals)")
plt.grid(True); plt.tight_layout(); plt.savefig("power.png", dpi=150); plt.show()
#送電線に流れる電流解析
plt.figure(); plt.plot(ts, I_mag); plt.xlabel("t [s]"); plt.ylabel("|I| [pu]")
plt.title("Line/Load Current"); plt.grid(True); plt.tight_layout()
plt.savefig("current.png", dpi=150); plt.show()
結果
以下、プログラムを実行した結果の要点を示す。
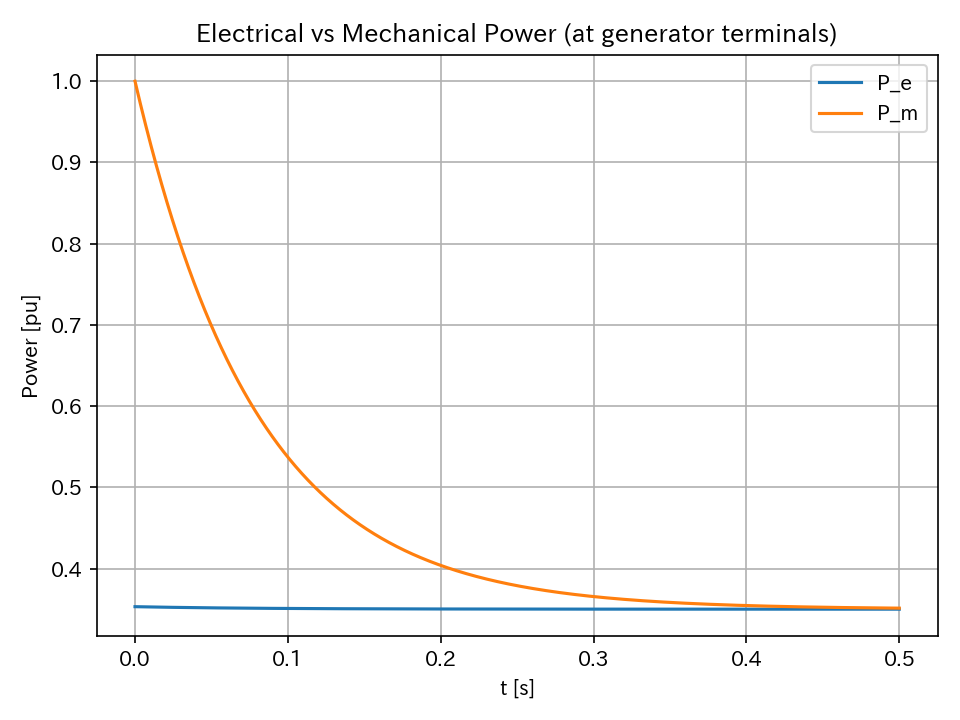
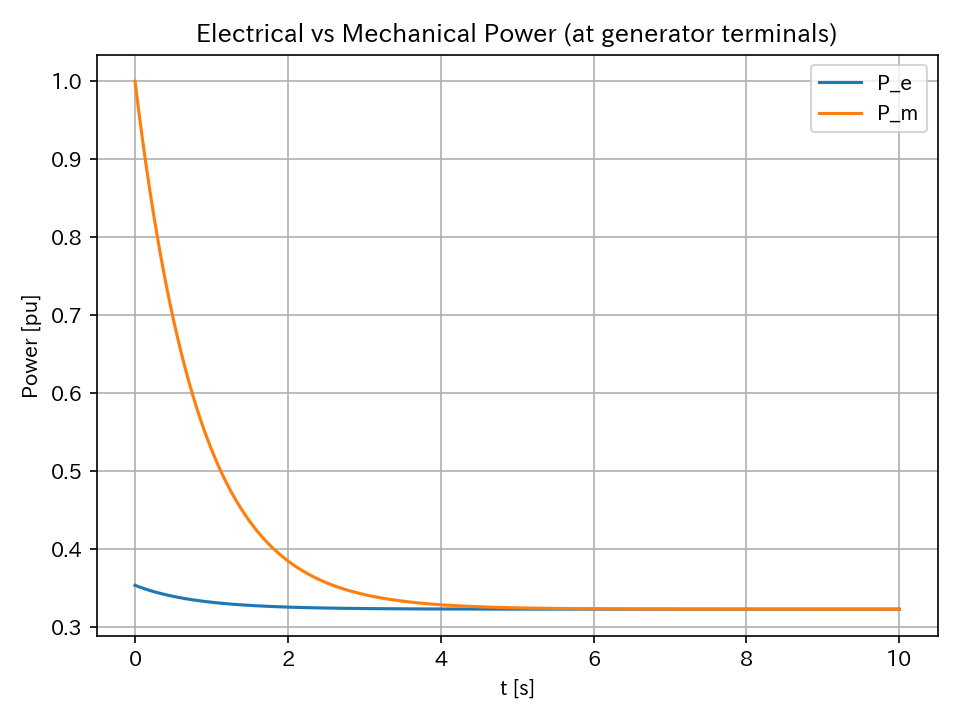
発電機の電気的出力と機械的入力の関係
上記のグラフのように、電力供給が需要に追従していることが分かる。
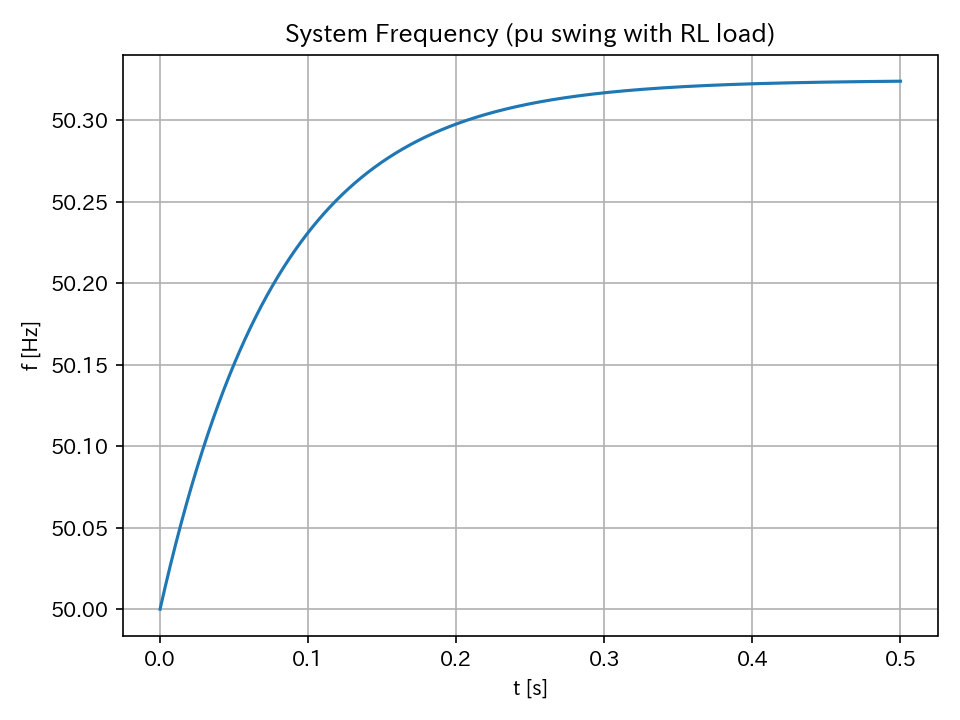
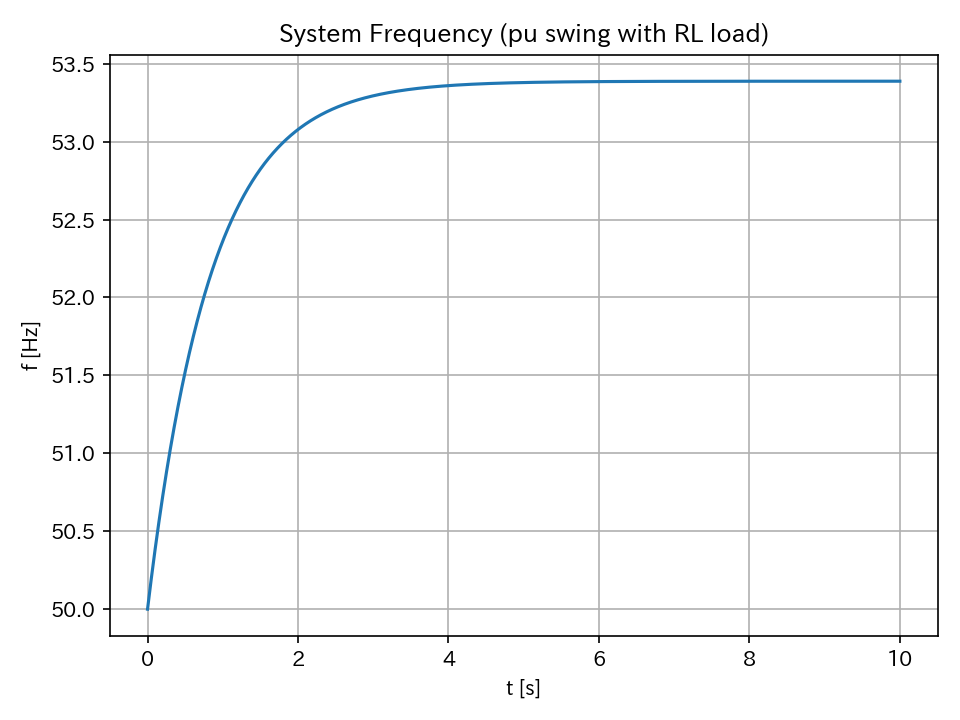
周波数特性
系統周波数が上昇した場合、発電機の機械的入力を減らすことで系統を安定化できていることが分かる。
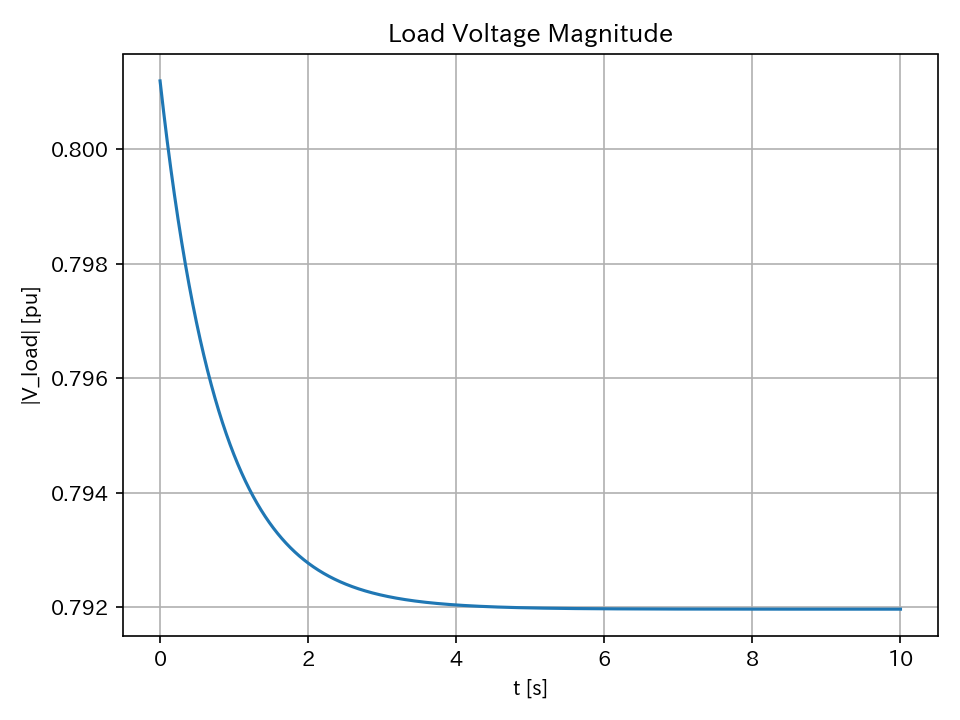
系統電圧の大きさ
供給力の増加に伴う周波数上昇を抑えるために、ガバナフリー制御が供給力を抑制する方向に働いた。
したがって、系統の電圧は徐々に低下していった。
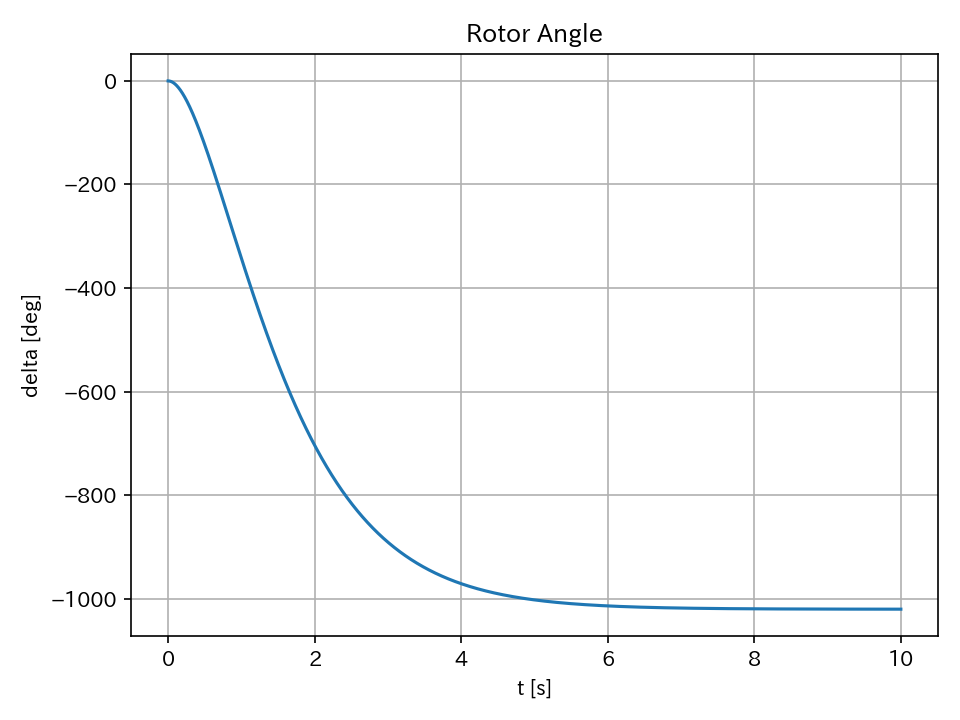
電圧位相差
このように、徐々に増加していってしまった。
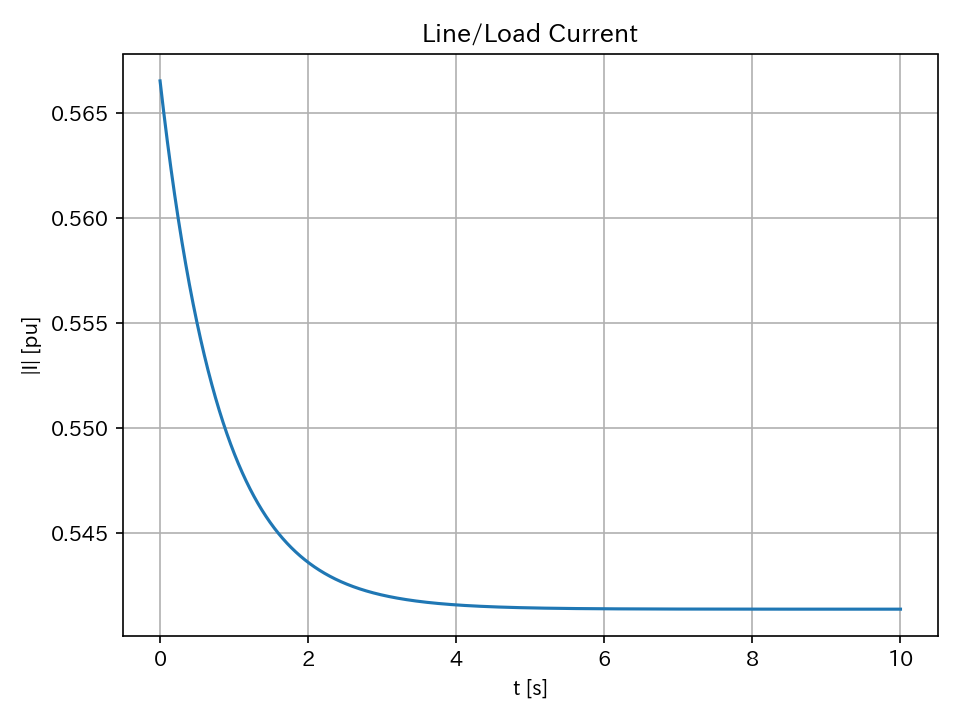
送電線に流れる電流
送電線に流れる電流についても、系統電圧と同様に徐々に低下したが、一定値に収束した。
まとめ
今回は、最も単純な電力系統モデルの過渡応答を解析した。結果、シンプルな挙動を示したが系統としての役割は最低限果たせたようである。今回扱った、知識は電力工学でもかなり重要なので、しっかりと抑えておき、自分の知識として自由自在に扱えるようにしたい。
参考文献
動揺方程式について
ルンゲクッタ法について