リサージュ曲線と周波数測定

はじめに

2つの周波数が異なる正弦波を入力として、x,y平面に図示するとリサージュ曲線という神秘的な曲線が描写される。この曲線は2つの信号の周波数や位相差に依存する。したがってその曲線の形状をもとにして、2つの信号の周波数の差や位相差を推定することが可能になる。今回は、以下のようなリサージュ曲線を描写することができるかをPythonを用いて調査する。

導入

リサージュ曲線とは

時刻$t$を媒介変数表示として、以下に表される曲線のことをいう。

\begin{equation}
\left\{ \,
    \begin{aligned}
    & x = Asin(2\pi nf t ) \\
    & y = Bsin(2\pi mf t +\alpha)  \\
    \end{aligned}
\right.
\end{equation}

ただし、$x$を位相の基準として、$A,B$を振幅として$f$を基準周波数とした。また、$n,m$を基準周波数の倍数とした。

プログラム

以下のようなプログラムをかいた。

python osiro.py

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import math
num=100
f=1
t=np.linspace(0,1/f,num)
#周波数（基準波の倍数）
n=2
m=1
#振幅
A=1
B=1
#位相差
alpha=0
x=A*np.sin(2*np.pi*(n*f)*t)
y=B*np.sin(2*np.pi*(m*f)*t+alpha*np.pi/180)

plt.plot(x,y)
plt.xlabel('x')
plt.ylabel('y')
plt.savefig("オシロスコープ_周波数測定_{}_{}_{}.png".format(n,m,alpha))
plt.show()

結果

これを実行すると以下のようなグラフが出力される。

周波数が同じで位相差が45度のとき

このように、楕円形になる。

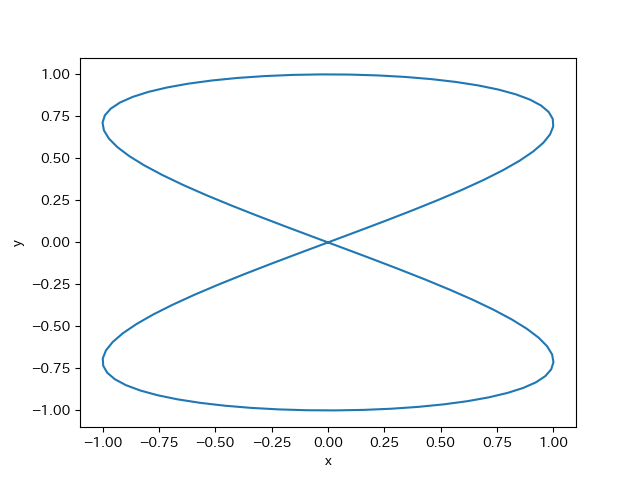
周波数が異なるとき

このように、綺麗なリサージュ曲線を描写することができた。

まとめ

今回は、Pythonを用いてリサージュ曲線をかくことができるかに挑戦した。結果、上手く描写することができ、リサージュ曲線の特別な場合が楕円形であるということも理解することができた。