ブリッジ回路と行列演算

はじめに

ブリッジ回路は、4本の回路素子と1つの回路素子を橋のようにつなげることからこのような名前がつけられている。回路素子に抵抗を用いた場合、対角の抵抗の積が等しくなるとき、中央の抵抗には電流が流れなくなるという性質がある。ゆえに、この性質を利用して、零位法という精密な測定に多用される。今回はわざとこの平衡条件を崩したときに、中央に流れる電流がどのような特性を示すのかについて考察する。また、交流回路のインピーダンスのときについても考察する。

ブリッジ回路とは

導入

以下のような電気回路をブリッジ回路と呼ぶ。

ここで、

R_1 R_4 = R_2 R_3

が成立するとき、

I=0

となる。これをブリッジ回路の平衡条件と呼ぶ

証明

$R_5$の両端にかかる電位差$V_d$について求めてみる。
分圧の法則から以下のようになる。

V_d=\frac{R_1}{R_1+R_3}V-\frac{R_4}{R_2+R_4}V

これが0になるとき

R_1 R_4 = R_2 R_3

が成立する。ただし、式を見て分かる通り、交流回路における複素インピーダンスを用いても上式のような関係は成立する。

中央に流れる電流

行列による表示

それでは、中央に流れる電流$I$について考察してみよう。
少し面倒だがキルヒホッフの法則により、以下のような式が成立する。

\begin{equation}
\left\{ \,
    \begin{aligned}
    & R_1 I_1 +R_3(I_1-I) = V \\
    & R_2 I_2+R_4(I+I_2) = V \\
    & R_1 I_1 + R_5 I =R_2 I_2
    \end{aligned}
\right.
\end{equation}

これを行列表示に置き換えると以下のようになる。

\begin{pmatrix}
V  \\
V  \\
0  \\
\end{pmatrix}


=

\begin{pmatrix}
R_1+R_3 & 0 & -R_3\\
0 & R_2+R_4 & R_4 \\
R_1 & -R_2 & R_5\\
\end{pmatrix}


\begin{pmatrix}
I_1  \\
I_2  \\
I  \\
\end{pmatrix}

ゆえに逆行列を用いてこれを解くと以下のようになる。

\begin{pmatrix}
I_1  \\
I_2  \\
I  \\
\end{pmatrix}


=

\begin{pmatrix}
R_1+R_3 & 0 & -R_3\\
0 & R_2+R_4 & R_4 \\
R_1 & -R_2 & R_5\\
\end{pmatrix}^{-1}


\begin{pmatrix}
V  \\
V  \\
0  \\
\end{pmatrix}

直流回路

それでは、直流電源を用いた場合、中央に流れる電流は抵抗$R_1$によってどの様に変化するのかをPythonを用いて考察する。

まず、以下のようなプログラムを作成する。

python bleadge_dc.py

#ブリッジ回路の抵抗を変化させたときの中心に流れる電流Iの大きさの変化
import matplotlib.pyplot as plt
import numpy as np
import japanize_matplotlib
#パラメーター設定
#初期条件
R_1=0
#定数
R_2=1
R_3=1
R_4=1
R_5=1
V=1
#グラフを作るとき用の空箱
x=[]
y=[]

#AI=V,I=A^-1V

for i in range(100):
    R_1=i/10
    A= [[R_1+R_3, 0, -R_3], [0, R_2+R_4, R_4],[R_1,-R_2,R_5]]
    #逆行列の生成
    I=np.linalg.inv(A)@[V,V,0]
    #print(I[2])
    x.append(R_1)
    y.append(abs(I[2]))
    
plt.xlabel("R_1抵抗値")
plt.ylabel("電流Iの大きさ")
    
plt.plot(x,y)
plt.show()

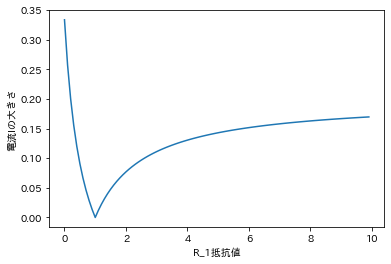
このように、ブリッジ回路の平衡条件が成立する$R_1=1$のとき、$I=0$となる。しかし、それ以外の場合では、急激に$I$の大きさが変化してしまうということが分かる。このような性質により、ブリッジ回路は精密な測定器具の抵抗計算などに使用される。

交流回路

交流回路の場合は、少し複雑になる。というのも、インピーダンスは実部と虚部から成立するからである。そこで、$R_1$の実部と虚部を独立に変化させていった場合において$I$の大きさはどの様に変化するのかを調べるために以下のプログラムを作った。

ただし、$R_1$を$\dot{Z_1}$のように置き換えるものとする。

python bleadge_AC.py

#ブリッジ回路の抵抗を変化させたときの中心に流れる電流Iの大きさの変化
import matplotlib.pyplot as plt
import numpy as np
import japanize_matplotlib
#パラメーター設定

#初期条件
Z_1=0
#パラメータ
Z_2=1+1j
Z_3=1
Z_4=1
Z_5=1
V=1

x=[]
y=[]

#AI=V,I=A^-1V
n=100

Z1_real = np.linspace(0,10,n)
Z1_imag = np.linspace(-10,10,n)

Z1_real,Z1_imag = np.meshgrid(Z1_real,Z1_imag)

I=np.zeros((n,n))

for i in range(n):
    for k in range(n):
        Z_1=Z1_real[i][k]+1j*Z1_imag[i][k]
        A= [[Z_1+Z_3, 0, -Z_3], [0, Z_2+Z_4, Z_4],[Z_1,-Z_2,Z_5]]
        #逆行列の生成
        I_vector=np.linalg.inv(A)@[V,V,0]
        I[i][k]=abs(I_vector[2])
        #print(I[i][k])
        


plt.xlabel("Z_1抵抗値")
plt.ylabel("Z_1インダクタンス")
    
plt.contourf(Z1_real,Z1_imag,I , cmap="jet")
plt.colorbar(label="電流Iの大きさ")
plt.show()

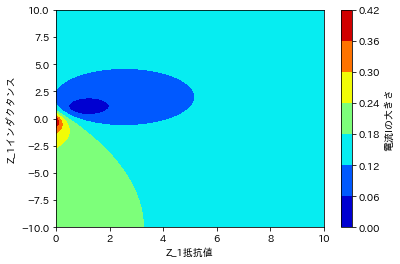
以下のような画像が出力される。

$\dot{Z}=1+j$のとき回路が平衡するため$|I|=0$となり最小値をとる。しかし、平衡条件からズレた瞬間に急激に電流の大きさは変化するということが分かる。また、$|I|=0$となる場合は、平衡条件のときのみであるということも分かった。

まとめ

今回は、ブリッジ回路の抵抗やインピーダンスを平衡条件から変化させたときの中央の電流の大きさがどのように変わるのかするのかを調べた。結果、平衡条件からずれた瞬間に急激に電流の大きさが変化した。このような、微小な変化を基準値からの大きなズレとして評価する特性を活かして精密な測定などに使用される。