はじめに
点電荷によって生じる電場と電位は、クーロンの法則によって数式化することができる。また、電位を微分してマイナスにすると電場になるという性質もある。そこで、今回は、点電荷の電位と電場をPythonで描写することを目的とする。
電位
点電荷によって生じる電位は以下のように表すことができる。
V(r)=\frac{q}{4\pi \epsilon (r-r_0)}
ただし$r$は観測点の存在する位置とし、 $r_0$は電荷の位置であるとする。
電場
次に、電場の定義は以下のように表すことができる。
\textbf{E}=-\frac{dV}{dr}
これは、ベクトルなので二次元平面空間では、以下のように表すことができる。
E_x=-\frac{dV}{dx},E_y=-\frac{dV}{dy}
プログラム
1つの正の点電荷
そこで、以下のようなプログラムを組む。
import math
import numpy as np
import matplotlib.pyplot as plt
#円周率
PI = math.pi
#プロットの生成数
n=100
#微小変化分
h= 1.0*10**-6
#等間隔に数直線上に点を配置する
x= np.linspace(-10,10,n)
y= np.linspace(-10,10,n)
#格子状に点を配置する
X,Y=np.meshgrid(x,y)
#電位
V= np.zeros((n,n))
#電場
Ex= np.zeros((n,n))
Ey= np.zeros((n,n))
#位置
x1=0
y1=0
#真空の誘電率
epsilon = 8.85*10**-12
#電荷
q1=1
#点電荷に生じる電位
def Potential(a,b):
return q1/(4*PI*((a-x1)**2+(b-y1)**2)**0.5)
for i in range(n):
for k in range(n):
x= X[i][k]
y= Y[i][k]
V[i][k]= Potential(x,y)
#hを用いた微分の定義より、電場を求める
Ex[i][k]= -(Potential(x+h,y)-Potential(x,y))/h
Ey[i][k]= -(Potential(x,y+h)-Potential(x,y))/h
#電位分布 n本の等高線
plt.contour(X,Y,V,n)
#電場分布
plt.streamplot(X,Y,Ex,Ey)
plt.show()
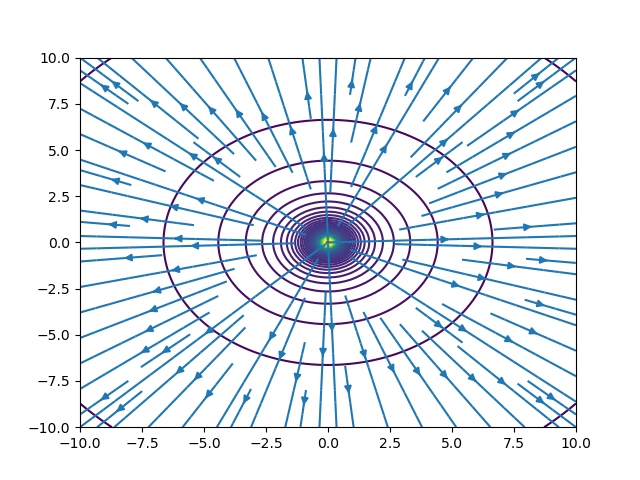
等高線が等電位面であり、ベクトル場が電場である。このように、電場と等電位面は直交する。
2つの正の電荷
import math
import numpy as np
import matplotlib.pyplot as plt
#円周率
PI = math.pi
#プロットの生成数
n=100
#微小変化分
h= 1.0*10**-6
#等間隔に数直線上に点を配置する
x= np.linspace(-10,10,n)
y= np.linspace(-10,10,n)
#格子状に点を配置する
X,Y=np.meshgrid(x,y)
#電位
V= np.zeros((n,n))
#電場
Ex= np.zeros((n,n))
Ey= np.zeros((n,n))
#位置
x1=-5
y1=0
x2=5
y2=0
#真空の誘電率
epsilon = 8.85*10**-12
#電荷
q1=1
q2=1
#点電荷に生じる電位
def Potential(a,b):
return q1/(4*PI*((a-x1)**2+(b-y1)**2)**0.5)+q2/(4*PI*((a-x2)**2+(b-y2)**2)**0.5)
for i in range(n):
for k in range(n):
x= X[i][k]
y= Y[i][k]
V[i][k]= Potential(x,y)
#hを用いた微分の定義より、電場を求める
Ex[i][k]= -(Potential(x+h,y)-Potential(x,y))/h
Ey[i][k]= -(Potential(x,y+h)-Potential(x,y))/h
#電位分布 n本の等高線
plt.contour(X,Y,V,n)
#電場分布
plt.streamplot(X,Y,Ex,Ey)
plt.show()
同符号の場合、電場は交わらない。
2つの異符号の点電荷
import math
import numpy as np
import matplotlib.pyplot as plt
#円周率
PI = math.pi
#プロットの生成数
n=100
#微小変化分
h= 1.0*10**-6
#等間隔に数直線上に点を配置する
x= np.linspace(-10,10,n)
y= np.linspace(-10,10,n)
#格子状に点を配置する
X,Y=np.meshgrid(x,y)
#電位
V= np.zeros((n,n))
#電場
Ex= np.zeros((n,n))
Ey= np.zeros((n,n))
#位置
x1=-5
y1=0
x2=5
y2=0
#真空の誘電率
epsilon = 8.85*10**-12
#電荷
q1=1
q2=-1
#点電荷に生じる電位
def Potential(a,b):
return q1/(4*PI*((a-x1)**2+(b-y1)**2)**0.5)+q2/(4*PI*((a-x2)**2+(b-y2)**2)**0.5)
for i in range(n):
for k in range(n):
x= X[i][k]
y= Y[i][k]
V[i][k]= Potential(x,y)
#hを用いた微分の定義より、電場を求める
Ex[i][k]= -(Potential(x+h,y)-Potential(x,y))/h
Ey[i][k]= -(Potential(x,y+h)-Potential(x,y))/h
#電位分布 n本の等高線
plt.contour(X,Y,V,n)
#電場分布
plt.streamplot(X,Y,Ex,Ey)
plt.show()
異符号の場合は、電場は正から負の向きへのベクトル場となる。
まとめ
今回は、点電荷の電場と電位についてPYthonを用いたプログラムによって描写することを試みた。結果、上手く描写することができたが、それには、等高線プロットと流線ベクトルの描写用の関数であるcontour,streamplotを用いた。これらを駆使することによって他にも綺麗な図を描くことができるので興味のある方は使用してみることをおすすめする。