はじめに
コンピュータを用いた解析の得意分野として行列の計算があるが、行列はその特性上膨大な情報を扱うことができる。したがって、様々な要素が変化し複雑に絡み合うシミュレーションにおいては行列を用いたシミュレーションが威力を発揮する。そこで、今回は現代制御工学の状態方程式を用いてRCL直列回路の入力電圧に対するコンデンサの電圧(出力電圧)を解析することにより、二次遅れ系の減衰係数の役割について考察する。具体的には、入力電圧をインパルス電圧、ステップ電圧、ランプ電圧と変化させていったときの応答について考察する。
以下簡単に結果の概略について述べる。
まず、3つの応答の特徴として入力に対して時間差を置いて追従しているということがうかがえる。また、減衰係数が高くなる程、制動力が働き、振動をする傾向がなくなる。
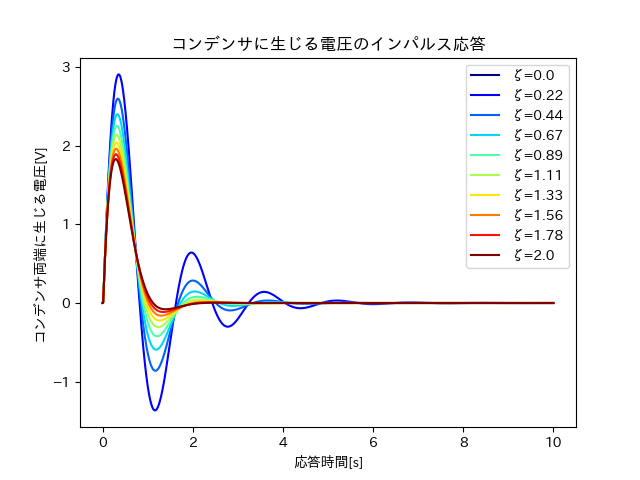
例えば、一瞬だが撃力であるインパルス応答では、一瞬だけ値が大きくなるがその後は緩やかに振動している。そして時間が十分に経過すれば0に収束していく。
一方で、ステップ応答では入力と同様に0より大きい定常偏差に収束するような挙動が見受けられる。
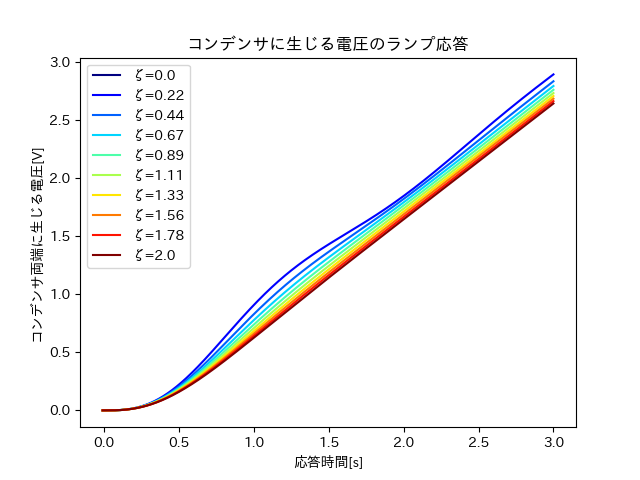
最後に、ランプ応答では入力の時間に対する比例関数に応答し、追従している様子がうかがえる。
問題設定
のような回路設定を考える。入力電圧をインパルス、ステップ、ランプと変化させていくことを考える。入力電圧が決定されればコンデンサに流れる電流が求まる。したがって、コンデンサに蓄えられる電荷が求められるので、静電容量で除することで、コンデンサ両端の出力電圧を求めることができる。今回は、コンデンサ出力電圧の時系列応答を減衰係数を変化させることで、調査する。
微分方程式
本章では、上の回路からキルヒホッフの法則を用いて微分方程式を立式して、状態方程式に変換する過程を述べる。
導入
コンデンサの電荷qさえ求められれば、コンデンサ両端に生じる電圧v曲線は以下のようにして求められる
v_{out}(t)=\frac{q(t)}{C}
したがって、以下のような微分方程式をまずは考える。
微分方程式と状態方程式
RLC直列回路の微分方程式は以下のようになる。ただし、電源電圧とコンデンサに蓄積された電荷の瞬時値をそれぞれ$e(t),q(t)$とした。
e(t)=R\frac{dq(t)}{dt}+L\frac{d^2 q(t)}{dt^2}+\frac{q(t)}{C}
ゆえに、
\frac{d^2 q(t)}{dt^2}=-\frac{q(t)}{LC}-\frac{R \frac{dq(t)}{dt}}{L}+\frac{e(t)}{L}
これを状態方程式にすると以下のようになる。
\begin{pmatrix}
\frac{dq(t)}{dt} \\
\frac{d^2 q(t)}{dt^2} \\
\end{pmatrix}
=
\begin{pmatrix}
0 & 1 \\
-\frac{R}{L} & -\frac{1}{CL} \\
\end{pmatrix}
\begin{pmatrix}
q(t) \\
\frac{d q(t)}{dt} \\
\end{pmatrix}
+
\begin{pmatrix}
0 \\
\frac{1}{L} \\
\end{pmatrix}
e(t)
したがって、以下のように表す。
\dot{\textbf{x}}(t)
=
\begin{pmatrix}
0 & 1 \\
-\frac{R}{L} & -\frac{1}{CL} \\
\end{pmatrix}
\textbf{x(t)}
+
\begin{pmatrix}
0 \\
\frac{1}{L} \\
\end{pmatrix}
e(t)
ただし、
\textbf{x}(t)=\begin{pmatrix}
q(t) \\
\frac{d q(t)}{dt} \\
\end{pmatrix}
\dot{\textbf{x}}(t)=\textbf{v}(t)=
\begin{pmatrix}
\frac{dq(t)}{dt} \\
\frac{d^2 q(t)}{dt^2} \\
\end{pmatrix}
とする。
ここで、位置ベクトル、速度ベクトルをそれぞれ$\textbf{x}(t),\dot{\textbf{x}}(t)$として、差分法で微分方程式を解くことを考える。
この条件のもとで、
I(t)=\frac{dq(t)}{dt}
を求める。
アルゴリズム
上記で得られた微分方程式(状態方程式)を解くアルゴリズムは以下の通りである。
ここでは、ある物体がx軸に対して直線運動していると考える。
変位と速度(差分法の原理)
微小区間($t=t$から$t=t+\Delta t$)に速度$v(t)$(変位の微分)と変位$x(t)$が以下のよう与えられたとする。
$x(t+\Delta t)$は微分の定義式から以下のように考えることができる。
これは、$t=t$のときの情報のみを頼りに$t=t+\Delta t$のときの情報を推定することができることを意味している。
\textbf{x}(t+\Delta t)=\textbf{x}(t)+\textbf{v}(t)\Delta t
これを$t=0$から$t=t$まで加算することで$t=t$での位置$\textbf{x}(t)$を求めることができる。
二次遅れ系への変換
導入
上の微分方程式や状態方程式はあくまでもRLC回路の3つのパラメータであるR,L,Cが決定されないと議論を進めることができない。
したがって、RLCの回路パラメータを二次遅れ系の固有角速度と減衰係数へと変換させるために、以下のような考察を行った。
変換式について
$RLC$回路の素子のパラメータと減衰係数、固有角速度$\zeta,\omega_n$の関係式を導出する。
より、
\zeta=\frac{R\sqrt{C}}{2\sqrt{L}},\omega_n=\sqrt{\frac{1}{LC}}
となる。これより、
C=\frac{\zeta}{R \omega_n}
L=(\frac{1}{\omega_n \sqrt{C}})^2
と、減衰係数、固有角速度$\zeta,\omega_n$を用いて$L,C$を$R$の式で表すことができる。
入力について
単位インパルス、単位ステップ、単位ランプ関数を以下のように定義する。
単位インパルス関数
$\delta(t)$は$t=0$付近のときに、刹那だが値が無限大とみなせるほどに十分大きな値になると定義する。また、時間軸における信号の面積は1となる。
単位ステップ関数
$u(t)$は$t<0$のときは0であり、$t\ge 0$のときは1とする関数であるものとする。
単位ランプ関数
$r(t)$は$t<0$のときは0であり、$t\ge 0$のときはtとする関数であるものとする。
プログラムと解析結果
前提条件として$0\le \zeta \le 2$の範囲で$\zeta$を動かすものとする。この値は、二次遅れ系の応答値が発散しないようにするために定めたものである。
インパルス応答
上記の考察より、以下のようなプログラムを作成した。
プログラム
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import math
#グラフの描写でJetを使用する
cm_name = 'jet'# B->G->R
cm = plt.get_cmap(cm_name)
omega_n=4 # 固有角周波数
def simu(jita):
# 微分方程式:V =R Q'*L Q''+Q/C
#パラメータ
#jita= 0.2 # 減衰係数
R = 10 # 抵抗値
C = (jita)**0.5/(R*omega_n) # 静電容量
L = (1/(omega_n*(C**0.5)))**2 # インダクタンス
e=100 # 入力電圧
#初期条件 (電荷と電荷の微分量つまり電流について)
x=np.array([0,0])
#初期時間
t=-0.01
#時間と状態量(ここでは電荷と電荷の微分量)
time_ary=[]
X=[]
#微小時間の時間間隔(小さくするほど精度は上がるが計算時間が比例して増大する)
delta_t=0.001
while(t<10):
#入力電圧
#E=np.sin(2*math.pi*50*t)
if 1/e>t>=0: # 1/eの時間だけ入力電圧をかける(1/e<delta_tだと取り込めないので注意する)
E=e
else:
E=0
v=np.array([[0, 1], [-1/(L*C),-R/L]])@x+np.array([0,1/L])*E
#位置の微小変化
x=x+v*delta_t
#print(v)
#演算結果を記録
time_ary.append(t)
#コンデンサの電荷からコンデンサ両端に生じる電圧を求める
X.append(x[0]/C)
#時間の更新
t=t+delta_t
plt.plot(time_ary,X,label="ζ="+str(round(jita,2)),color=cm(jita/2))
jita_ary=np.linspace(0,2,num=10)
for jita in jita_ary:
simu(jita)
plt.legend()
plt.xlabel("応答時間[s]")
plt.ylabel("コンデンサ両端に生じる電圧[V]")
plt.title("コンデンサに生じる電圧のインパルス応答")
#グラフを保存する
plt.savefig("RLC_状態方程式_インパルス応答電圧.png")
#グラフの表示
plt.show()
ステップ応答
上記の考察より、以下のようなプログラムを作成した。
プログラム
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import math
#グラフの描写でJetを使用する
cm_name = 'jet'# B->G->R
cm = plt.get_cmap(cm_name)
omega_n=4 # 固有角周波数
def simu(jita):
# 微分方程式:V =R Q'*L Q''+Q/C
#パラメータ
#jita= 0.2 # 減衰係数
R = 10 # 抵抗値
C = (jita)**0.5/(R*omega_n) # 静電容量
L = (1/(omega_n*(C**0.5)))**2 # インダクタンス
e=100 # 入力電圧
#初期条件 (電荷と電荷の微分量つまり電流について)
x=np.array([0,0])
#初期時間
t=-0.01
#時間と状態量(ここでは電荷と電荷の微分量)
time_ary=[]
X=[]
#微小時間の時間間隔(小さくするほど精度は上がるが計算時間が比例して増大する)
delta_t=0.001
while(t<10):
#入力電圧
#E=np.sin(2*math.pi*50*t)
if t>=0:
E=e
else:
E=0
v=np.array([[0, 1], [-1/(L*C),-R/L]])@x+np.array([0,1/L])*E
#位置の微小変化
x=x+v*delta_t
#print(v)
#演算結果を記録
time_ary.append(t)
#コンデンサの電荷からコンデンサ両端に生じる電圧を求める
X.append(x[0]/C)
#時間の更新
t=t+delta_t
plt.plot(time_ary,X,label="ζ="+str(round(jita,2)),color=cm(jita/2))
jita_ary=np.linspace(0,2,num=10)
for jita in jita_ary:
simu(jita)
plt.legend()
plt.xlabel("応答時間[s]")
plt.ylabel("コンデンサ両端に生じる電圧[V]")
plt.title("コンデンサに生じる電圧のステップ応答")
#グラフを保存する
plt.savefig("RLC_状態方程式_ステップ応答電圧.png")
#グラフの表示
plt.show()
ランプ応答
上記の考察より、以下のようなプログラムを作成した。
プログラム
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import math
#グラフの描写でJetを使用する
cm_name = 'jet'# B->G->R
cm = plt.get_cmap(cm_name)
omega_n=4 # 固有角周波数
def simu(jita):
# 微分方程式:V =R Q'*L Q''+Q/C
#パラメータ
#jita= 0.2 # 減衰係数
R = 10 # 抵抗値
C = (jita)**0.5/(R*omega_n) # 静電容量
L = (1/(omega_n*(C**0.5)))**2 # インダクタンス
e=1 # 入力電圧
#初期条件 (電荷と電荷の微分量つまり電流について)
x=np.array([0,0])
#初期時間
t=-0.01
#時間と状態量(ここでは電荷と電荷の微分量)
time_ary=[]
X=[]
#微小時間の時間間隔(小さくするほど精度は上がるが計算時間が比例して増大する)
delta_t=0.0001
while(t<3):
#入力電圧
#E=np.sin(2*math.pi*50*t)
if t>=0:
E=e*t
else:
E=0
v=np.array([[0, 1], [-1/(L*C),-R/L]])@x+np.array([0,1/L])*E
#位置の微小変化
x=x+v*delta_t
#print(v)
#演算結果を記録
time_ary.append(t)
#コンデンサの電荷からコンデンサ両端に生じる電圧を求める
X.append(x[0]/C)
#時間の更新
t=t+delta_t
plt.plot(time_ary,X,label="ζ="+str(round(jita,2)),color=cm(jita/2))
jita_ary=np.linspace(0,2,num=10)
for jita in jita_ary:
simu(jita)
plt.legend()
plt.xlabel("応答時間[s]")
plt.ylabel("コンデンサ両端に生じる電圧[V]")
plt.title("コンデンサに生じる電圧のランプ応答")
#グラフを保存する
plt.savefig("RLC_状態方程式_ランプ応答電圧.png")
#グラフの表示
plt.show()
まとめ
今回は、3つのタイプの入力に対して二次遅れ系がどのような応答を示すのかを調査した。具体的には、減衰係数を0から2まで変化させることで、振動を抑える制動力が3つの場合すべてに共通して働くということがわかった。また、インパルス応答は収束値が0になった。一方でステップ応答では収束値が定数になった。しかし、ランプ応答だけ、特定の値に収束することはなかった。このことから、いずれの場合の出力も入力に追従して応答しているということがわかる。
このような解析では、複雑な線形代数の数値計算を行うことができるコンピュータが有利となる。したがって行列である状態方程式を扱う現代制御と相性が良い。しかし、手計算や値が未知数の変数として計算をせねばならない場合は、柔軟性が高い古典制御(ラプラス変換、部分分数展開、ラウス・フルビッツの判別法など)を視野に入れて考えるといい。
参考文献
ステップ応答について
状態方程式について
matplotlibのカラーマップについて