はじめに
三角関数は、奥が深い。三角比のsinとcosは兄弟のような関係をしているように思えるが、tanだけ仲間外れのような関係である。なので、受験の定石上では、tanはあまり使わずsinとcosの対称関係を用いるのが主流である。しかし、tanを用いると、sinとcosの2変数関数を1変数関数とみなせる場合があるなどのメリットも存在する。
そこで、今回は、$t=\tan \frac{\theta}{2} $とおいたとき、
\sin \theta =\frac{2t}{1+t^2}
\cos \theta =\frac{1-t^2}{1+t^2}
と表されるという有名事項を用いた証明問題を2題行うことで、二次関数や軌跡の分野領域を復習する。
2倍角の公式の導入
2倍角の公式を少し変形した式は以下のように与えられる。
\sin \theta =2\sin\frac{\theta}{2} \cos\frac{\theta}{2}
\cos \theta =2{\cos}^2 \frac{\theta}{2}-1
この式は、すぐに書けるよう証明も含めて覚えておこう。
正接の関係式
一方で、忘れやすいのが三角関数の相互関係の$\tan$の場合である。一応導出方法を軽く紹介する。
有名な$\sin,\cos$の相互関係の式をまずは考える。
\sin^2\theta+\cos^2\theta=1
この式の両辺を$\cos^2\theta$で割ると$\tan^2\theta$がでてくるので、そのことだけ覚えておく。
\frac{\sin^2\theta}{\cos^2\theta}+\frac{\cos^2\theta}{\cos^2\theta}=\frac{1}{\cos^2\theta}
したがって、
\tan^2\theta+1=\frac{1}{\cos^2\theta}
このことは、意外と盲点になりやすく文系理系関わらず覚えておくと便利である。(数3の積分などで使用する)
三角比の媒介変数表示
さて、本題である。
t=\tan \frac{\theta}{2}
とおくと、
\sin \theta =2\sin\frac{\theta}{2}\cos\frac{\theta}{2}=2\tan\frac{\theta}{2}\cos^2\frac{\theta}{2}=2\tan\frac{\theta}{2}(1+\tan^2\frac{\theta}{2})^{-1}=\frac{2t}{1+t^2}
となる。一方で、
\cos \theta =2\cos^2 \frac{\theta}{2}-1=2(1+\tan^2\frac{\theta}{2})^{-1}-1=\frac{2}{1+t^2}-1=\frac{1-t^2}{1+t^2}
二次関数の最小最大値問題
さて、上記の式を用いて以下の式を証明しよう。
-1\le sin\theta,\cos\theta \le 1
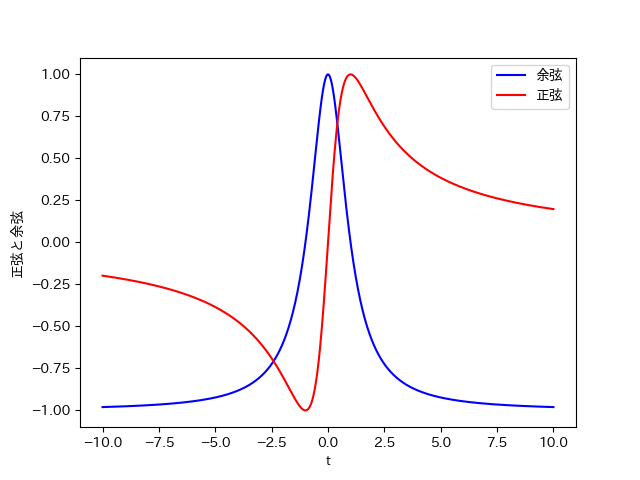
参考までに、各媒介変数表示で表現されるグラフを以下に示しておく。
このグラフの概形が30秒くらいで分かると数3においては難関大合格レベルだと思う。
(ちなみに筆者は偶関数か奇関数くらいしか分からなかった。)
余弦の場合
まずは簡単な$\cos\theta$からである。
\cos \theta =\frac{2}{1+t^2}-1
なので、$1+t^2\ge1$より、
0\le \frac{2}{1+t^2}\le1
が成立する。したがって、
-1 \le\cos \theta \le1
正弦の場合
微積分を用いてもいいのだが、逆像法(受験数学では逆手流?)を用いる。つまり実数解の存在条件を用いる。
\sin \theta =\frac{2t}{1+t^2}
ゆえに、$(1+t^2)>0$より分母を払い整理すると以下のようになる。
(\sin\theta) t^2-2t+\sin\theta=0
これは、$t$の二次方程式とみなすことができる。そこで、$t$が実数解を持つような条件を調べる。判別式を$D/4$とおくと、
D/4=1-\sin^2\theta\ge 0
ゆえに、
-1\le sin\theta \le 1
となる。(ちなみに、受験とは関係ないが上記の考察から、$t$の範囲を実数から複素数に拡張すれば、上記の範囲を逸脱することができる。)
円の軌跡の問題
問題
以下の媒介変数$t$によって描かれる軌跡を求めよ。
\begin{equation}
\left\{ \,
\begin{aligned}
& x = \frac{1-t^2}{1+t^2} \\
& y = \frac{2t}{1+t^2} \\
\end{aligned}
\right.
\end{equation}
ただし、大人の都合上$x>-1$とする。つまり、$t\le \infty$とする。
まずは、無難に$x$の式を変形する。
t^2=\frac{1-x}{1+x}
これを$y$の式に代入して整理すると以下のようになる。
y=t(1+x)
両辺を二乗すると、
y^2=t^2(1+x)^2
となるので、$t^2=\frac{1-x}{1+x}$を代入して整理すると、
y^2=(1-x)(1+x)
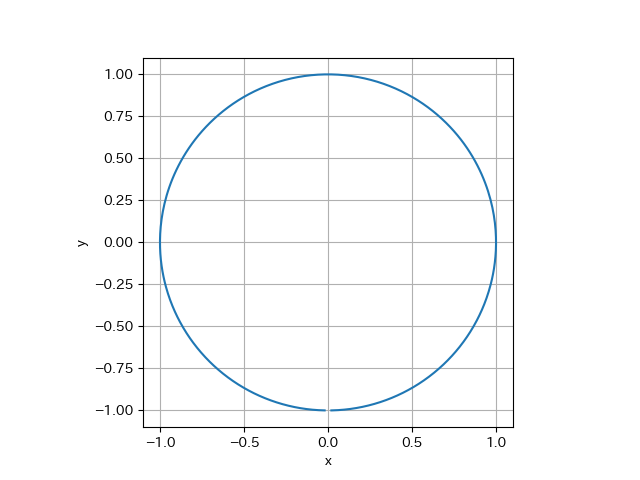
より、円の軌跡である
x^2+y^2=1
を描く。ただし、$x>-1$となる。
プログラム
補足としてプログラムを書いた。
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import math
n=10000
L=100
t=np.linspace(-L,L,n)
x=(1-t**2)/(1+t**2)
y=2*t/(1+t**2)
#縦軸と横軸を等間隔にする
plt.axes().set_aspect("equal")
#補助線を引く
plt.grid()
plt.plot(x,y)
plt.xlabel('x')
plt.ylabel('y')
plt.savefig("円の軌跡.png")
plt.show()
まとめ
今回は、三角関数の公式と軌跡に関する問題を扱った。これらの融合問題は入試によくでるので、背景を含めてしっかりと理解しておくことをお勧めする。特に実数解の存在条件や軌跡の範囲はよく狙われるので注意することが大切である。