磁場中での電荷の運動

はじめに

磁場中での電荷の運動は一般的に円運動もしくはらせん運動になることが知られている。円運動になる理由は、ローレンツ力が向心力としてはたらくためである。一方、古典力学において初期条件さえ与えられれば、加速度$a$から速度$v$と変位$x$は求められる。そこで今回は、微小変化する区間では加速度一定の等加速度運動をすると仮定して、運動方程式を立てて、そこから速度と位置を導出することによって、磁場中の電荷がらせん運動をすることを観察することを目的とする。

向心力

向心力としてのローレンツ力は磁束密度$\textbf{B}$と速度$\textbf{v}$が与えられていた場合、以下のように表すことができる。

\textbf{F}=q\textbf{v}\times\textbf{B}

これが、向心力となるので、初速度$v$、半径$r$とすると

m \frac{v^2}{r}=qvB

r=\frac{mv}{qB}

と表すことができる。

速度と変位

微小区間($t=t$から$t=t+\Delta t$)に粒子の加速度$\textbf{a}$が与えられたとき
速度と変位は以下のように表すことができる。これは、微分の定義から来ている。

\textbf{v}(t+\Delta t)=\textbf{v}(t)+\textbf{a}(t)\Delta t

\textbf{x}(t+\Delta t)=\textbf{x}(t)+\textbf{v}(t)\Delta t

これを$t=0$から$t=t$まで加算することで$t=t$での位置$\textbf{x}(t)$を求めることができる。

プログラム

これをもとにして、プログラムを考えると以下のようになる。

python rasen.py

import numpy as np
import matplotlib.pyplot as plt

#パラメータ
B=np.array([0,0,1])
q=1.0
m=1.0
#初期条件 (x,v,a)=(位置,速度,加速度)
x=np.array([1,0,0])
#斜め上に発射
v=np.array([0,1,1])

a=np.array([-1,0,0])

#3次元のグラフ（散布図）を描くための設定
fig = plt.figure()
ax = fig.add_subplot(projection='3d')

#初期時間
t=0
#微小時間の時間間隔(小さくするほど精度は上がるが計算時間が比例して増大する)
delta_t=0.01
while(t<10):
    #速度の微小変化
    v=v+a*delta_t
    #位置の微小変化
    x=x+v*delta_t
    #ローレンツ力によって生じる加速度,cross(v,B)はvとBの外積である
    a=-(q/m)*np.cross(v, B)

    #時間の更新
    t=t+delta_t
    #print(x)
    #粒子の位置を記録
    ax.scatter(x[0], x[1], x[2], color='blue')
#グラフを保存する
plt.savefig("rasen.png")
#グラフの表示
plt.show()

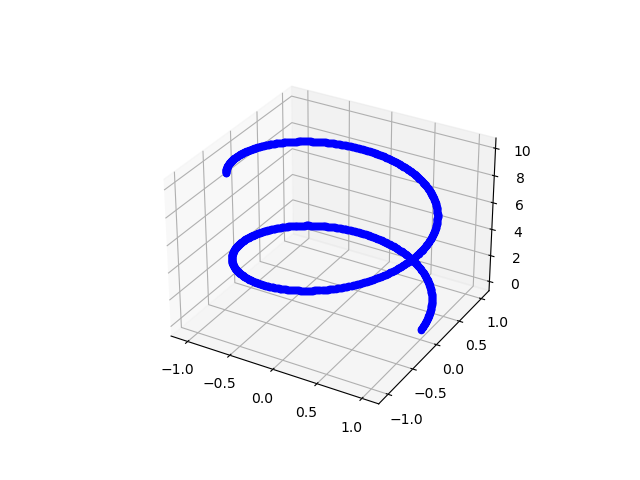
これを実行すると以下のようになる。

うまく、描写することができていることが分かる。

まとめ

今回は、プログラムを用いて、磁場に関して斜めに入射した場合の電荷の運動についてシミュレーションした。結果らせん運動をするということが分かった。これは、ローレンツ力から加速度を求め、それを積分することで速度と変位を求めて計算した。