はじめに
円周角の定理の逆は円の軌跡を描くということを証明するためにかなりの頻度で使用される。したがって幾何学的な意味で重要である。しかし、解析学的な点からいえば、かなりの計算量を節約して円の存在を証明することができる。そこで、今回は円周角の定理の逆を複素数平面を用いて解析的に証明することを目的とする。そして、その定理を元に以下のような円の一部をPythonを用いて作図する。
円周角の定理の逆について
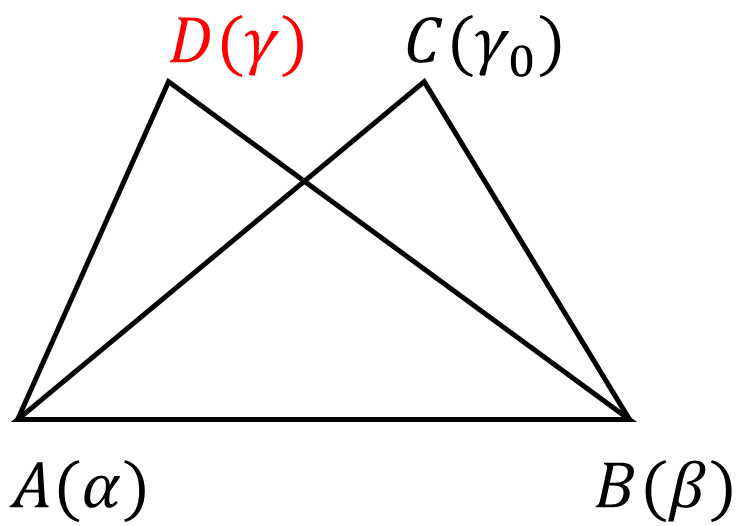
以下の図で考える。
固定な3点で形成される$\Delta ABC$と動点$D$を考える。
$\angle ACB=\angle ADB$を常に満たすように動点$D$を移動させる。そうすると、$D$の軌跡は、円周角の定理の逆より、円周上にあるはずである。
複素数平面
$\angle ACB=\angle ADB$を常に満たすことから、以下のことが成立する。
\frac{\beta-\gamma}{\alpha-\gamma}=k\frac{\beta-\gamma_0}{\alpha-\gamma}
ただし$k$は実数である。
これを$k$ について解くと以下のようになる。
\frac{\beta-\gamma}{\alpha-\gamma}=k\frac{\beta-\gamma_0}{\alpha-\gamma}
k=\frac{(\beta-\gamma)(\gamma_0-\alpha)}{(\beta-\gamma_0)(\gamma-\alpha)}
ここで、任意の実数$k$について、以下の式が成立する。
k=\bar{k}
したがって、
\frac{(\beta-\gamma)(\gamma_0-\alpha)}{(\beta-\gamma_0)(\gamma-\alpha)}=
\overline{\frac{(\beta-\gamma)(\gamma_0-\alpha)}{(\beta-\gamma_0)(\gamma-\alpha)}}
これを整理すると、以下のようになる。
(\beta-\gamma)(\gamma_0-\alpha)(\bar{\beta}-\bar{\gamma_0})(\bar{\gamma}-\bar{\alpha})=
(\beta-\gamma_0)(\bar{\beta}-\bar{\gamma})(\bar{\gamma}-\bar{\alpha})(\gamma-\alpha)
ここで、複素数$A=(\gamma_0-\alpha)(\bar{\beta}-\bar{\gamma_0})$とおくと以下のように式変形を行うことができる。
(A+\bar{A})\gamma\bar{\gamma}+(A\bar{\alpha}-\bar{A}\bar{\beta})\gamma+(-\bar{A}\alpha+A \beta)\bar{\gamma}+(A\bar{\alpha}\beta+\bar{A}\alpha \bar{\beta})=0
ここで、$-\bar{A}\alpha+A \beta=\overline{A\bar{\alpha}-\bar{A}\bar{\beta}}$の関係性があるので、
\gamma \bar{\gamma}-\bar{p}\gamma-p\bar{\gamma}+q=0
と表すことができる。($p$は複素数であるが$q$は実数である。)
(\gamma-p)(\overline{\gamma-p})=-q+|p|^2
|\gamma-p|=\sqrt{-q+|p|^2}
となり、これは円の方程式を表す。(半径が正になるかどうかの議論は今回は式が複雑になりそうなので省略した。いい方法をご存じの方は教えていただきたいです。)
プログラム
\frac{\beta-\gamma}{\alpha-\gamma}=k\frac{\beta-\gamma_0}{\alpha-\gamma}
の式を$\gamma$について整理すると以下のようになる。
\gamma=\frac{k\alpha(\beta-\gamma_0)+\beta(\gamma_0-\alpha)}{k(\beta-\gamma_0)+(\gamma_0-\alpha)}
上式を用いて、実数$k$を変化させたときの$\gamma$を描写するプログラムを作成した。
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import math
m=3
n=1000
k=np.linspace(-m,m,n)
alpha=1
beta=-1
gamma_0=3+3j
gamma=((k-1)*alpha*beta+gamma_0*(beta-k*alpha))/((k*beta-alpha)+gamma_0*(1-k))
plt.axis('equal')
plt.plot([alpha.real,beta.real,gamma_0.real,alpha.real],[alpha.imag,beta.imag,gamma_0.imag,alpha.imag])
plt.plot(gamma.real,gamma.imag)
plt.savefig("円周角の定理の逆.png")
plt.show()
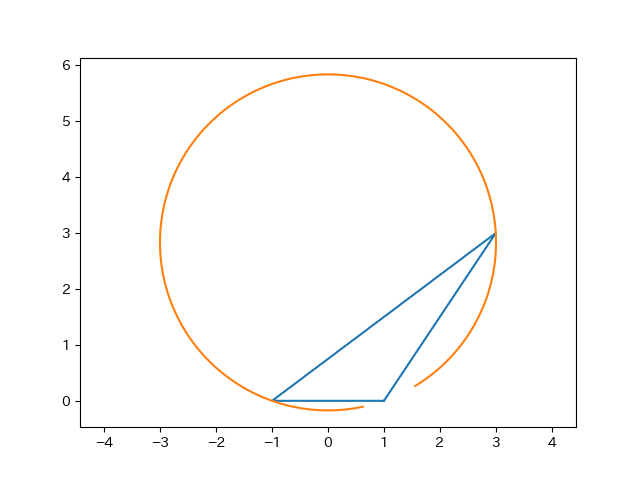
これを実行すると、以下のようなグラフが出力される。
このように、実数$k$を変化させることで円周の一部を描写することができる。
まとめ
今回は、円周角の定理の逆を解析学的に証明することを試みた。具体的には、各座標の特性を複素数で表して、角度の情報を数式に直して議論した。後半ではpythonを用いて円周の一部を描写していることを確認した。このように、円周角の定理を解析学的に証明するのは、かなり面倒である。
したがって、幾何学的な性質を上手く利用できることが分かれば、積極的に利用することで計算量をかなり低減させることができる。