はじめに
連続かつ周期性のある関数は、三角関数の無限級数の和によって表現することが知られている。これをフーリエ解析という。今回はこれを応用して、方形波の電圧をRC直列回路やRL直列回路に印加した場合の電流の過渡応答についてフーリエ解析を用いて調査することを目的とする。具体的には、Pythonを用いて、方形波電圧を三角関数で表される交流に分割して、それぞれの場合について個々の電流を求めて、最終的にそれを重ね合わせの理によって合成する。
方形波
方形波電圧は、三角関数の無限和で表すことができる。ただし、プログラムでは無限和を適切に表現することが難しいので、有限和で表し近似する。
方形波を表現するプログラムとして以下のようなプログラムを書いた。
from scipy import signal#方形波を作るのに使用
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import math
V=1
n= int(input("和の回数を入力してください"))
x = np.arange(0.0, 2*math.pi, 0.02)
y=0
for num in range(n):
y=y+(1/(2*num+1))*np.sin((2*num+1)*x)
y=y*(4*V/math.pi)
plt.plot(x, y,color="red", label="フーリエ変換")
y2 = signal.square(x)
plt.plot(x, y2,color="blue", label="方形波")
plt.title('フーリエ変換:方形波,n='+str(num+1))
plt.legend() #凡例
#グラフを画像として保存
plt.savefig('フーリエ変換' +str(num+1)+ ".png")
plt.show()
積算数
積算数nを上げると正確さがその様に増すのかを調査する。
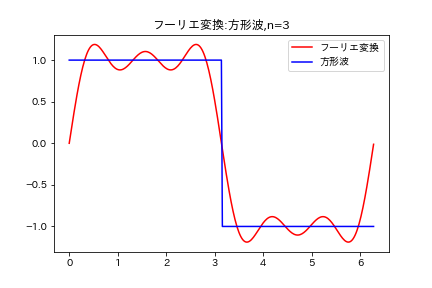
n=3 のとき
正確さには欠けるが、概形は描けているようである。
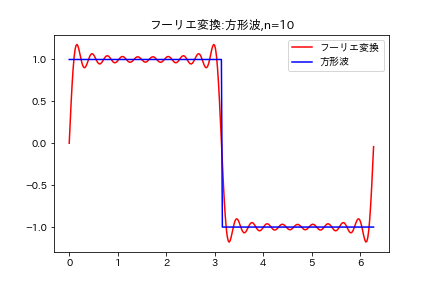
n=10 のとき
n=3のときと比較して上手く近似できているようであるが、ノイズが多いようである。
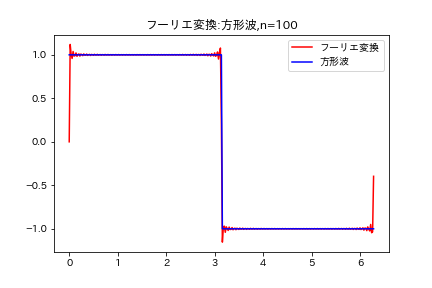
n=100 のとき
n=100のとき、ほぼ近似できていることが分かる。
過渡応答
次に、上記のようなプログラムによって電圧を作成して、それに対応するRL回路やRC回路の電流を求めてみる。
具体的な流れとしては、
1.方形波電圧を正弦波交流電圧の有限和で表す
2.それぞれの正弦波交流電圧に対応する電流を求める
3.それらを加算することで電流の過渡応答について調査する
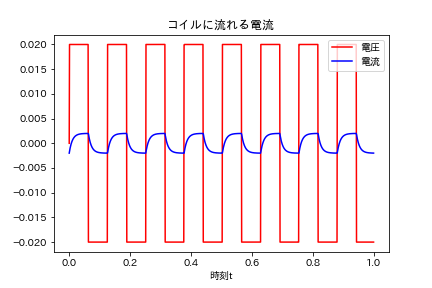
RL回路
以下のようなプログラムを書いた。
過渡応答
from scipy import signal#方形波を作るのに使用
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import math
V=1
#積算数
n= 100000
t = np.arange(0.0, 1, 0.001)
y1=0
y2=0
L=0.1
R=10
omega=50
for num in range(n):
y1=y1+(1/((2*num+1)*omega))*np.sin((2*num+1)*omega*t)
y2=y2+(1/((2*num+1)*omega))*np.sin((2*num+1)*omega*t-np.arctan((2*num+1)*omega*L/R))/(R**2+((2*num+1)*omega*L)**2)**0.5
y1=y1*(4*V/math.pi)
y2=y2*(4*V/math.pi)
plt.plot(t, y1,color="red", label="電圧")
#y2 = signal.square(t)
plt.plot(t, y2,color="blue", label="電流")
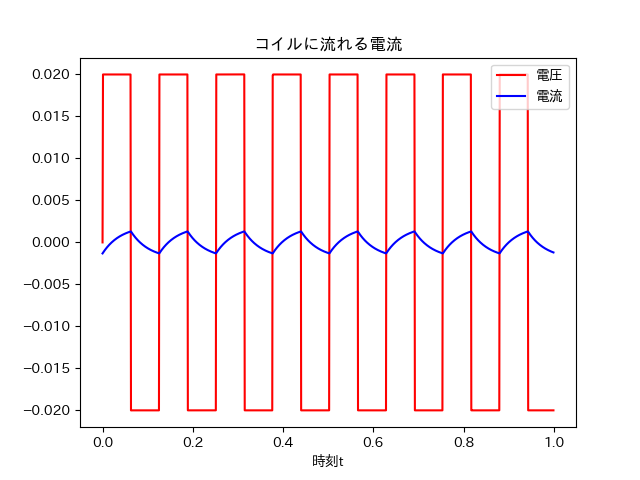
plt.title('コイルに流れる電流')
plt.xlabel('時刻t')
plt.legend() #凡例
plt.savefig("過渡応答コイルと抵抗.png")
plt.show()
チョッパ回路の原理
さて、LがRと比較して割合的に十分大きくなるときの波形について以下に示す。
L=0.4のとき
電流に注目して欲しい。上がりと下がりは一次遅れで表されるが、マクローリン展開により$exp(x)=1+x (|x|<<1)$と示せるため、ほぼ三角波と近似することができるため、抵抗に生じる電圧の平均値の近似値を簡単に求めることができる。
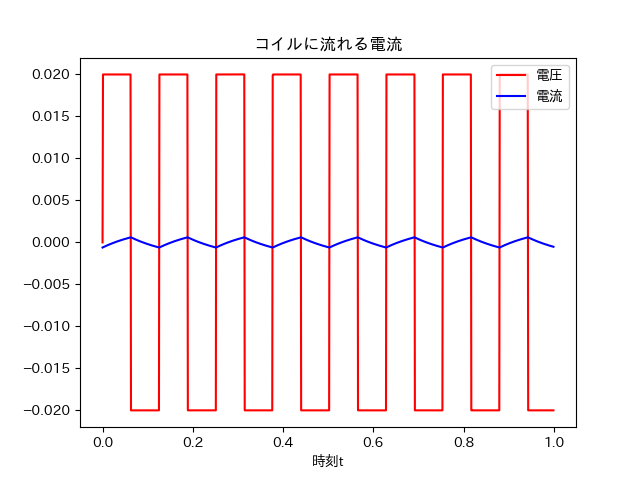
L=1.0のとき
このように、さらにLを大きくすれば、より三角波に近づく。
RC回路
以下のようなプログラムを書いた。
from scipy import signal#方形波を作るのに使用
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import math
V=1
#積算数
n= 100000
t = np.arange(0.0, 1, 0.001)
y1=0
y2=0
C=0.001
R=10
omega=50
for num in range(n):
y1=y1+(1/((2*num+1)*omega))*np.sin((2*num+1)*omega*t)
y2=y2+(1/((2*num+1)*omega))*np.sin((2*num+1)*omega*t+np.arctan(((2*num+1)*omega*C*R)**-1))/(R**2+((((2*num+1)*omega*C)**-1)**2))**0.5
y1=y1*(4*V/math.pi)
y2=y2*(4*V/math.pi)
plt.plot(t, y1,color="red", label="電圧")
#y2 = signal.square(t)
plt.plot(t, y2,color="blue", label="電流")
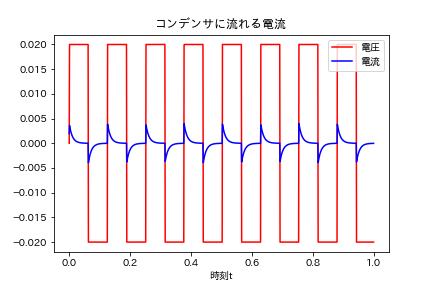
plt.title('コンデンサに流れる電流')
plt.xlabel('時刻t')
plt.legend() #凡例
plt.savefig("過渡応答コンデンサと抵抗.png")
plt.show()
グラフよりコンデンサは、直流を一瞬だけ流すという性質を垣間見ることができる。
まとめ
フーリエ解析を用いてRL回路やRC回路といった一次遅れ系の過渡応答の電流解析をおこなった。結果、積算数を十分に大きくすれば、ほぼ適切な近似をすることが可能になるということが分かった。また、積算数が増えるほど、一次のオーダで計算時間が増えると考えられるが、今回のプログラムは、個人用のPCでも実行が可能であった。