はじめに
等角写像法という、複雑な形状の導体によって生じる電場と電位分布を求める手法がある。まず、単純な形状の導体をある変換を用いて複雑な形状の導体に写像できると仮定しよう。その上で単純な形状の導体によって生じる電場と電位分布も同時に写像する。その分布は求めたいものと一致するはずである。今回は、半直線上の導体によって生じる電位、電場分布が実際の電場と電位分布と一致するかどうかを検証する。
問題設定(電験1種理論)
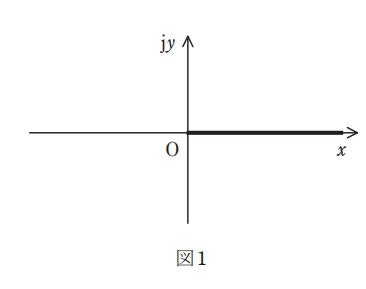
以下のような導体棒に正の電荷を与えたときの電場と電位分布を求めたい。(電験1種理論令和4年問1)
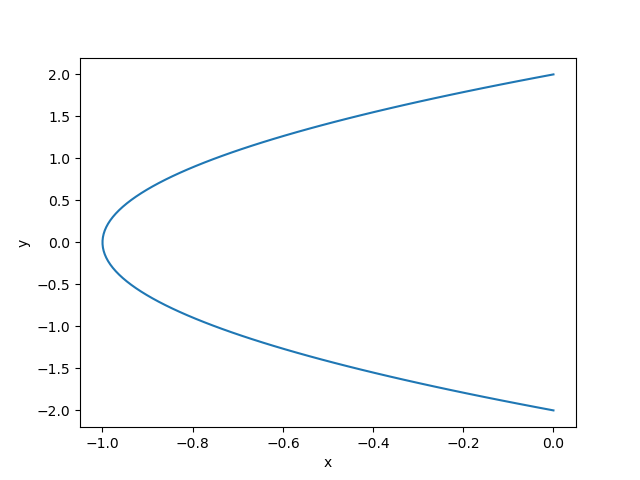
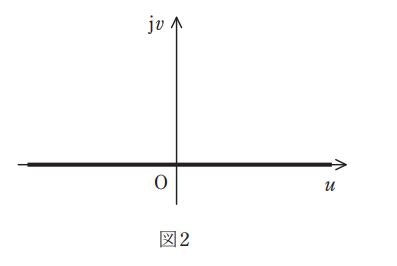
このグラフ($y=0,x>0$)は、$f(w)=w^2$つまり、$x+jy=(u+jv)^2$によって$v=0$(u:実数全体)を移した結果となる。
したがって、$f$を逆変換すると、
\begin{equation}
\left\{ \,
\begin{aligned}
& u = \pm Real(x+jy)^{0.5} \\
& y = \pm Imag(x+jy)^{0.5} \\
\end{aligned}
\right.
\end{equation}
これを利用する。ただし、今回は簡単にするため+のときのみで考える。
数式解析
写像前の電位と電場の分布について考える。
$y=0$(x:全実数)という領域において胴体棒が存在する。
電位分布
代数解析
したがって、写像前の電位は$v=k$(k:0を除く定数)と考えられるので、
\begin{equation}
\left\{ \,
\begin{aligned}
& x = u^2-k^2 \\
& y = 2ku \\
\end{aligned}
\right.
\end{equation}
と表せるので、
x = (\frac{y}{2k})^2-k^2=\frac{y^2}{4k^2}-k^2
プログラム
これをプログラムすると以下のようになる。
ただし$v=1$とした。
import numpy as np
import matplotlib.pyplot as plt
#写像前の(u,v)空間 (無限棒の設定)
u=np.linspace(-1,1,100)
v=1
w=u+1j*v
#写像
f_w=w**2
z=f_w
#z=x+jy
x=z.real
y=z.imag
plt.xlabel("x")
plt.ylabel("y")
plt.plot(x,y)
plt.show()
電場分布
代数解析
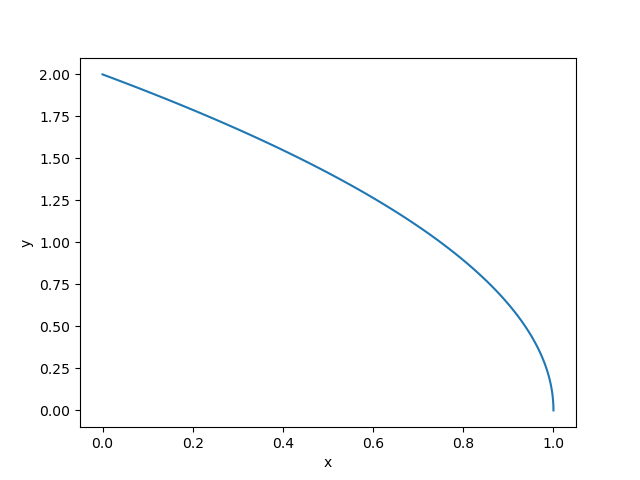
$u=k,(k>0)$としたときの$x,y$の関係について考える。
\begin{equation}
\left\{ \,
\begin{aligned}
& x = k^2-v^2 \\
& y = 2kv \\
& v > 0
\end{aligned}
\right.
\end{equation}
したがって、
x= -\frac{y^2}{4k^2}+k ,(y>0)
プログラム
import numpy as np
import matplotlib.pyplot as plt
#写像前の(u,v)空間 (無限棒の設定)
u=1
v=np.linspace(0,1,100)
w=u+1j*v
#写像
f_w=w**2
z=f_w
#z=x+jy
x=z.real
y=z.imag
plt.xlabel("x")
plt.ylabel("y")
plt.plot(x,y)
plt.show()
これは、電位の分布つまり等電位面と直交する。
プログラム
次に、以下二種類のプログラムにより電位と電場分布を求める。
写像を用いた解法
上の図によって生じる電場の概要は以下のようになり、半径方向(y方向)にのみ依存する。
Qの電荷を導体に加えたときの電場は以下の式で表すことができる。
ただし、$\lambda$は電荷密度である。
E_{xy}(y)=-\frac{dV_{xy}(y)}{dy}=-\frac{\lambda}{2\pi \epsilon y}
これは、ガウスの法則より明らかである。
次に、積分をして電位を求めると以下のようになる。
ただし、y=aは基準電位面である。
V_{xy}(y)=-\int^{y}_{a}{E_{xy}(y)}dy=-\frac{\lambda}{2\pi \epsilon} log(\frac{|y|}{a})
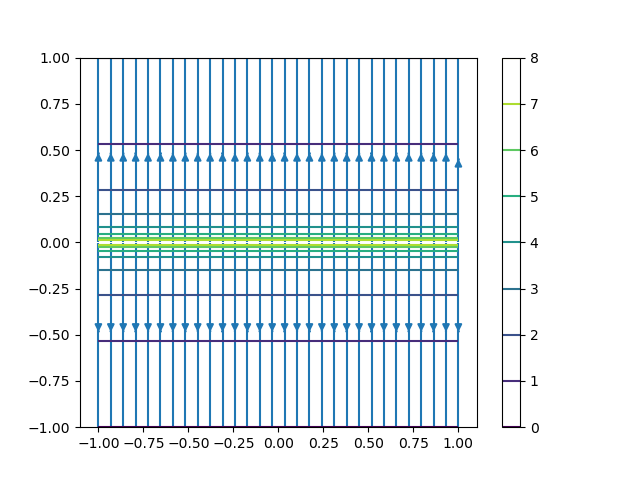
さて、そのことについてプログラムを書くと以下のようになる。
import numpy as np
import matplotlib.pyplot as plt
import math
#微小変化分
h=1.0*10**-6
n=100
x=np.linspace(-1,1,n)
y=np.linspace(-1,1,n)
X,Y = np.meshgrid(x,y)
lam= 10
epsilon=1
a=1
def V_xy(y):
return -(lam/(2*math.pi*epsilon))*np.log(abs(y/a))
#V=-(lam/(2*math.pi*epsilon))*np.log(Y/a)
V=np.zeros((n,n))
Ex=np.zeros((n,n))
Ey=np.zeros((n,n))
for i in range(n):
for p in range(n):
V[i][p]=V_xy(Y[i][p])
Ey[i][p]=-(V_xy(Y[i][p]+h)-V_xy(Y[i][p]))/h
plt.streamplot(X,Y,Ex,Ey)
plt.contour(X,Y,V)
plt.colorbar()
plt.savefig("無限大導体棒の電場と電位.png")
plt.show()
等電位面と電場は直行しているということが分かる。
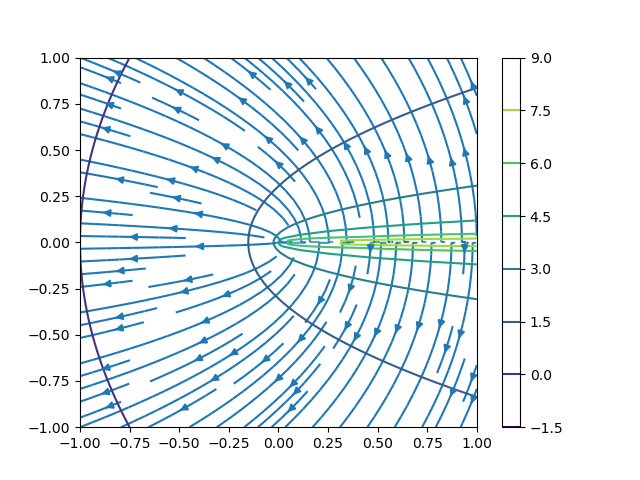
この図を導体が半直線の場合に変換するプログラムは以下のようになる。
import numpy as np
import matplotlib.pyplot as plt
import math
#微小変化分
h=1.0*10**-6
n=100
x=np.linspace(-1,1,n)
y=np.linspace(-1,1,n)
X,Y = np.meshgrid(x,y)
lam= 10
epsilon=1
a=1
def fai_xy(y):
return -(lam/(2*math.pi*epsilon))*np.log(abs(y/a))
#V=-(lam/(2*math.pi*epsilon))*np.log(Y/a)
fai=np.zeros((n,n))
Ex=np.zeros((n,n))
Ey=np.zeros((n,n))
for i in range(n):
for p in range(n):
#座標変換(+の解を採用)
#u=((X[i][p]+1j*Y[i][p])**0.5).real
v=((X[i][p]+1j*Y[i][p])**0.5).imag
fai[i][p]=fai_xy(v)
v_hx=(((X[i][p]+h)+1j*Y[i][p])**0.5).imag
v_hy=((X[i][p]+1j*(Y[i][p]+h))**0.5).imag
Ex[i][p]=-(fai_xy(v_hx)-fai_xy(v))/h
Ey[i][p]=-(fai_xy(v_hy)-fai_xy(v))/h
plt.streamplot(X,Y,Ex,Ey)
plt.contour(X,Y,fai)
plt.colorbar()
plt.savefig("写像後半無限棒の電場と電位.png")
plt.show()
等電位面と電場は直行しているということが分かる。
点電荷の集合とみなした解法
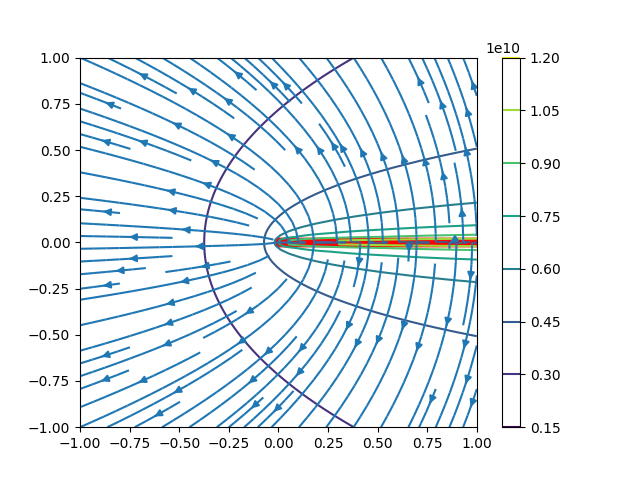
上記の考察によって得られた電位と電場の分布が正しいか調べるために、以下のようなプログラムを書いた。
具体的には以下のようなアルゴリズムである。
まず、$n$を十分に大きな値として$q$を微小分と仮定する。
1.$y=0(x>0)$上に等間隔な電荷密度$q$の赤色の点を$n$点だけ置く。
2.各点により生じる電位をクーロンの法則によって求める。
3.それらを足すことで、半直線状の導体によって生じる電位分布を求める。
4.電位分布から電場分布を求める。
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
coords,ds = np.linspace(-1,1,100,retstep=True)
#XY領域の作成
X,Y = np.meshgrid(coords,coords)
k = 9.0*10**9
n=1000
#微小区間の電荷の大きさ
q1=1/n
#電極の範囲(半直線として観測領域と比較して十分な長さとした)
x=np.linspace(0,10,n)
# 初期電位
Z=0
for i in range(n):
#電極の図示
plt.plot(x[i],0,'o',color='red')
#電位の計算
Z=Z+ k*q1/((X-x[i])**2+Y**2)**0.5
#電位のグラフ
plt.contour(X,Y,Z,)
plt.colorbar()
#勾配の配列は行方向、列方向の順で返されるので注意
#勾配つまり傾きを求める
dY,dX=np.gradient(Z,ds)
#電場
Ex=-dX
Ey=-dY
#電場のグラフ
plt.streamplot(X,Y,Ex,Ey)
# ax.quiver(X,Y,dX,dY)
# 描写範囲の限定
plt.xlim(-1,1)
plt.savefig("半直線導体とクーロンの法則による解析.png")
plt.show()
このように、鏡像法で求めた電位と電場分布と実際の分布は一致する。
まとめ
今回は、電験1種理論の等角写像法についてプログラミングを用いることで検証した。具体的には半直線の導体場合によって生じる電位と電場の分布を、写像を使った場合と点電荷の集合体とみなした場合を用いて解析した。結果、両者は一致した。このように、鏡像法は上手い写像方式さえ見つかれば、有限要素法などの解析よりも遥かに計算量が少なく済む。しかし、目的の写像をするために関数を見つけるのはかなり難しいと考えられる。なので、様々な方法と合わせて解析に用いることが最良の方法ではないかと考えられる。
参考文献