ミカエリス・メンテン式と数値計算

はじめに

化学反応は、複雑な挙動を示すものが多い。その現象を説明するために、単純なモデルで考える場合がある。特に、生物化学の場合は扱う分子のサイズが大きい有機物を扱うためどうしても複雑なモデルになりがちである。今回は、基質と酵素が結合し新たな生成物が形成される化学反応を一番単純なモデルで説明することを試みる。具体的には、まず化学の反応速度論を導入する。次に、酵素反応における重要概念であるミカエリス・メンテン式を紹介し、反応速度論により表される微分方程式を数値計算で解いたものと比較する。

酵素と基質のモデル

以下のように、酵素$E$と基質$S$が結合し、中間体$ES$になり、$E$と生成物$P$が生成するとする。

E+S \overset{k_1}{\underset{k_{-1}}{\rightleftharpoons}} ES \overset{k_2}{\longrightarrow}E+P

ただし、酵素と基質が結合し、中間体になる反応を平衡反応とし、瞬時に反応する一方で、中間体から生成物が反応する段階は律速段階とする。

反応速度論

反応速度は、反応物の濃度に比例すると考えると、以下のような微分方程式が成立する。

\begin{cases}
\frac{d}{dt} [ES]=k_1[E][S]-k_{-1}[ES]-k_2[ES]\\
\frac{d}{dt}[E]=k_{-1}[ES]-k_1[E][S]+k_2[ES]\\
\frac{d}{dt}[P]=k_2 [ES]\\
\frac{d}{dt}[S]=-k_1 [E][S] +k_{-1}[ES]\\
\end{cases}

ここで、平衡状態では、中間体$[ES]$はほぼ変化しないという仮定を用いると、

\frac{d}{dt}[ES]=0

が成立する。したがって、

[ES]=\frac{k_1}{k_{-1}+k_2}[E][S]=\frac{[E][S]}{k_m}

となる。$(k_m=\frac{k_{-1}+k_2}{k_1})$

ここで、酵素の一部が基質と結合して中間体になることから、初期の酵素濃度を$[E]_0$とすると、以下の式が成立する。

[E]_0=[E]+[ES]

ゆえに、

[ES]=\frac{[E]_0[S]}{k_m+[S]}

したがって、生成物$P$の反応速度$v_P$は以下のように表すことができる。

v_{P}=k_2[ES]=\frac{k_2[E]_0[S]}{k_m+[S]}

濃度の時間変化

さて、まずは以下の微分方程式を数値計算するプログラムを作成した。

\begin{cases}
\frac{d}{dt} [ES]=k_1[E][S]-k_{-1}[ES]-k_2[ES]\\
\frac{d}{dt}[E]=k_{-1}[ES]-k_1[E][S]+k_2[ES]\\
\frac{d}{dt}[P]=k_2 [ES]\\
\frac{d}{dt}[S]=-k_1 [E][S] +k_{-1}[ES]\\
\end{cases}

python concentration_time.py

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import math

t=0
t_ary=[]
dt=3.0*10**-4
t_max=30
V=[]
X=[]

k1=0.1
k_1=0.1
k2=0.03

E=3
S=3
ES=0
P=0

def v(ES,E,P,S):
  v_ES=k1*E*S-k_1*ES-k2*ES
  v_E=k_1*ES-k1*E*S+k2*ES
  v_P=k2*ES
  v_S=-k1*E*S+k_1*ES
  return np.array([v_ES, v_E, v_P, v_S])

while t < t_max:
  t += dt
  t_ary.append(t)
  v_ary = v(ES, E, P, S)
  V.append(v_ary)
  ES = ES+ v_ary[0] * dt
  E =E+ v_ary[1] * dt
  P =P+ v_ary[2] * dt
  S =S+ v_ary[3] * dt
  X.append([ES, E, P, S])
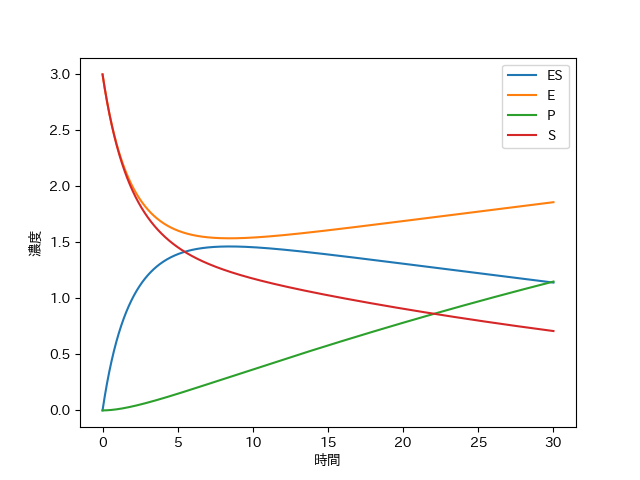
plt.plot(t_ary, [x[0] for x in X], label='ES')
plt.plot(t_ary, [x[1] for x in X], label='E')
plt.plot(t_ary, [x[2] for x in X], label='P')
plt.plot(t_ary, [x[3] for x in X], label='S')
plt.xlabel('時間')
plt.ylabel('濃度')
plt.legend()
plt.savefig('ミカエリスメンテン式_濃度_時間.png')
plt.show()  

このように、濃度は複雑な変化をするが、生成物$P$の生成量はほぼ比例のようなグラフとなり、一定の上昇率であがっていく。

ミカエリス・メンテン式

そこで、ミカエリス・メンテン式を確かめるために、初期基質濃度を変化させた解析を複数実行しそのときの$P$の反応をプロットするプログラムを以下のように作成した。

python Michaelis–Menten.py

import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
import math
t=0
dt=0.3*10**-4
t_max=0.1

V_P0_ary=[]
V_P0_ary_inv=[]
S_ary_inv=[]
k1=1
#k_{-1}=k_1で表す
k_1=1
k2=0.3
n=300
S_ary=np.linspace(0, 30, n)  # Sの値を0から3まで100点で生成
km=(k2+k_1)/k1
def v(ES,E,P,S):
  v_ES=k1*E*S-k_1*ES-k2*ES
  v_E=k_1*ES-k1*E*S+k2*ES
  v_P=k2*ES
  v_S=-k1*E*S+k_1*ES
  return [v_ES, v_E, v_P, v_S]

for i in range(n):
  S = S_ary[i]  # Sの値を更新
  S_ary_inv.append(1/S)  # Sの逆数を保存
  t=0
  E=3
  V_max=k2*E
  ES=0
  P=0
  t_ary=[]
  V=[]
  X=[]
  v_P=[]
  while t < t_max:
    t += dt
    t_ary.append(t)

    v_ary = v(ES, E, P, S)
    V.append(v_ary)
    ES = ES+ v_ary[0] * dt
    E =E+ v_ary[1] * dt
    P =P+ v_ary[2] * dt
    S =S+ v_ary[3] * dt
    #print(v_ary[2])
    v_P.append(v_ary[2])  # v_Pの値を保存
    X.append([ES, E, P, S])
  #print(v_P)  # v_Pの値を出力
  #V_P0_ary.append(V[2][0])  # v_Pの値を保存
  V_P0_ary.append(v_P[-1])  # v_Pの値を保存
  V_P0_ary_inv.append(1/v_P[-1])  # v_Pの逆数を保存

#plt.plot(t_ary, [x[0] for x in X], label='ES')
# plt.plot(t_ary, [x[1] for x in X], label='E')
# plt.plot(t_ary, [x[2] for x in X], label='P')
# plt.plot(t_ary, [x[3] for x in X], label='S')
# plt.xlabel('時間')
# plt.ylabel('濃度')
# plt.legend()
# plt.savefig('ミカエリスメンテン式_濃度_時間.png')
# plt.show()  

plt.plot(S_ary, V_P0_ary, label=' [S] vs v_P')
plt.plot(S_ary,V_max*S_ary/(km+S_ary), label='理論値')
plt.xlabel('[S]')
plt.ylabel('v_P')
plt.legend()
plt.savefig('ミカエリスメンテン式_S_vs_vP.png')
plt.show()

plt.plot(S_ary_inv, V_P0_ary_inv, label=' 1/[S] vs 1/v_P')
plt.xlabel('1/[S]')
plt.ylabel('1/v_P')
plt.legend()
plt.savefig('ラインウェーバー・バークプロット.png')
plt.show()

これを実行すると以下のようになった。

このように、少し、ミカエリス・メンテン式の理論値よりもずれてしまったが、おおむね理論通りだといえる。ずれた原因としては、微分方程式を解く際の数値計算で用いたオイラー法の精度が悪いこと、ミカエリス・メンテン式の近似計算によるずれなどが考えられる。

参考までに、ラインウェーバー・バークプロットも以下に示しておく。おおむね線形になった。

まとめ

酵素反応といった化学反応の濃度変化を時系列を追ってモデル化し解析するのはとても難しく、手計算ではまず無理だろう。だが、時系列の情報を排除し、基質の初期濃度と反応速度のみの関係性を近似計算を用いて調査することは手計算でもできる。これがミカエリス・メンテン式である。だが、その分時系列の情報を削いでいるため理解するのが難しいと思う。そこで、今回は計算機を用いて化学反応速度計算を行い、ミカエリス・メンテン式が正しいことを調査した。

参考文献