はじめに
古典力学や古典電磁気学の世界においてモデルは一般的に一次または二次程度の線形微分方程式を立てて運動を叙述することから始まる。特に、制御工学では古典的なモデルの運動や変位をどのようにして安定に保つのかということに熱意を注ぐ必要性がある。そこで、今回は電験一種の二次試験の機械・制御における現代制御の問題を扱うことにより、現代制御がどのようにして系を安定化させるのかという考え方の一例を示す。具体的には不安定な系を復元力に相当する入力を強制的に加えて安定化させるフィードバック制御について調査する。
モデル
モデルとしては、電験一種平成27年度二次試験機械・制御問4を参考にした。詳細な問題情報は電験王様を参照されたい。
\dot{\boldsymbol{x}}(t)=\boldsymbol{A}\boldsymbol{x}+\boldsymbol{b}u(t)
ただし、
\boldsymbol{A}
=
\begin{pmatrix}
-4 & -6 \\
3 & 5 \\
\end{pmatrix}
,
\boldsymbol{b}=
\begin{pmatrix}
-2\\
3 \\
\end{pmatrix}
,
\boldsymbol{x}=
\begin{pmatrix}
x_1\\
x_2 \\
\end{pmatrix}
で表されるものとする。
系の安定性について
$\boldsymbol{A}$の固有値は$-1,2$と正の実数が存在してしまうので不安定な系である。そこで$f=-kx$のような復元力を入力にフィードバックしてあげることで強制的に安定化させることについて考える。
u(t)=-\boldsymbol{f}\boldsymbol{x}(t)
ただし、
\boldsymbol{f}=(f_1,f_2)=(\frac{3}{4},\frac{13}{6})
とする。
プログラム
時間応答
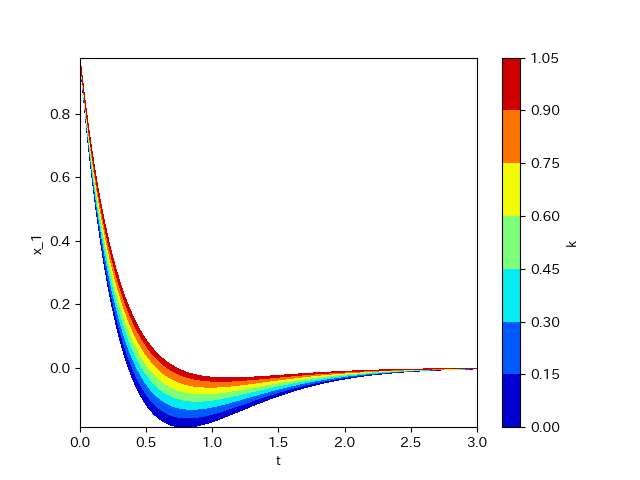
それでは、フィードバックを施した場合の時間応答を見ていこう。
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
A=np.array([[-4,-6],[3,5]])
b=np.array([-2,3])
f_1=np.array([3/4,13/6])
t_max=3
num=500
delta_t=t_max/num
def simu(k):
t=0
x_1=1
x_2=2
x_1_ary=[]
x_2_ary=[]
t_ary=[]
while t<t_max:
x=np.array([x_1,x_2])
u=-(f_1@x)*k
v=A@x+b*u
t_ary.append(t)
x=x+v*delta_t
t=t+delta_t
x_1=x[0]
x_2=x[1]
x_1_ary.append(x_1)
x_2_ary.append(x_2)
return t_ary,x_1_ary,x_2_ary
n=10
k_ary=np.linspace(0,1,10)
k_min=1.1
k_max=1.2
X=[]
Y=[]
Z=[]
for i in range(n):
k_0=k_ary[i]
k=k_min+(k_max-k_min)*k_0
t_ary,x_1_ary,x_2_ary,=simu(k)
X.append(t_ary)
Y.append(x_1_ary)
Z.append(k_0*np.ones(len(t_ary)))
plt.xlabel("t")
plt.ylabel("x_1")
plt.contourf(X,Y,Z,level=10,cmap="jet")
plt.colorbar(label="k")
plt.savefig("フィードバック制御の時間応答.png")
plt.show()
ただし、系の観察をしやすくするために、$u(t)=-k\boldsymbol{f}\boldsymbol{x}(t)$という実数$k$をおいた。
このように、$k$が大きいほど安定化しやすくなることがわかる。これは、復元力が大きければ大きいほど系のシステムの振動は小さくなり安定化しやすくなることを意味している。
入力と位置の関係
次に、入力を変化させていったとき着目物体の位置がどのように変化するのかを調査した。
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
A=np.array([[-4,-6],[3,5]])
b=np.array([-2,3])
f_1=np.array([3/4,13/6])
t_max=3
num=500
delta_t=t_max/num
def simu(k):
t=0
x_1=1
x_2=2
x_1_ary=[]
x_2_ary=[]
t_ary=[]
while t<t_max:
x=np.array([x_1,x_2])
u=-(f_1@x)*k
v=A@x+b*u
t_ary.append(t)
x=x+v*delta_t
t=t+delta_t
x_1=x[0]
x_2=x[1]
x_1_ary.append(x_1)
x_2_ary.append(x_2)
return t_ary,x_1_ary,x_2_ary
n=10
k_ary=np.linspace(0,1,10)
k_min=1.1
k_max=1.2
X=[]
Y=[]
Y_2=[]
Z=[]
for i in range(n):
k_0=k_ary[i]
k=k_min+(k_max-k_min)*k_0
t_ary,x_1_ary,x_2_ary,=simu(k)
X.append(t_ary)
Y.append(x_1_ary)
Y_2.append(x_2_ary)
Z.append(k_0*np.ones(len(t_ary)))
plt.xlabel("x_1")
plt.ylabel("x_2")
plt.contourf(Y,Y_2,Z,level=10,cmap="jet")
plt.colorbar(label="k")
plt.savefig("フィードバックの強さk.png")
plt.show()
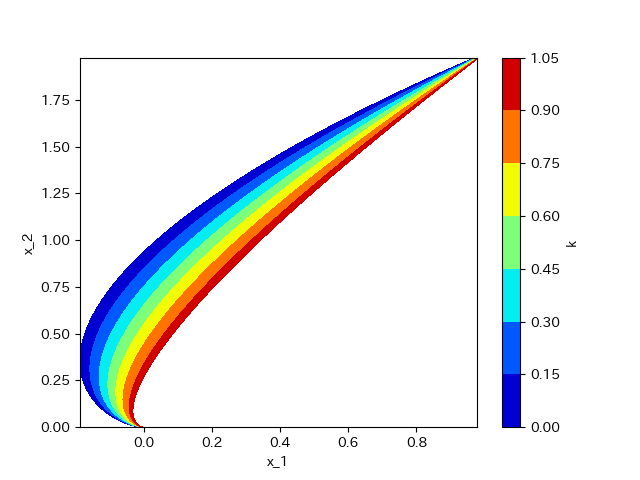
これを実行すると以下のようになる。
このように、復元力が異なると軌道が変わる傾向にある。しかし、原点に安定し、収束される場合は最終的に原点に収まるようである。
位置の変化と初期値について
さて、最後に初期値がどのように安定性に影響を与えるのかを見ていこう。今回の系ではそのような初期値であれ最終的には原点に収束することが分かっている。それを図示しようと思う。
前提条件として、$(x_1,x_2)$空間に半径が1となるような原点中心の円をプロットする。その円上にある点を初期値とおく。したがって、以下のようなプログラムが書ける。
import numpy as np
import matplotlib.pyplot as plt
import japanize_matplotlib
A=np.array([[-4,-6],[3,5]])
b=np.array([-2,3])
f_1=np.array([3/4,13/6])
t_max=3
num=500
delta_t=t_max/num
k=1.0
def simu(theta):
t=0
x_1=np.cos(theta)
x_2=np.sin(theta)
x_1_ary=[]
x_2_ary=[]
t_ary=[]
while t<t_max:
x=np.array([x_1,x_2])
u=-(f_1@x)*k
v=A@x+b*u
t_ary.append(t)
x=x+v*delta_t
t=t+delta_t
x_1=x[0]
x_2=x[1]
x_1_ary.append(x_1)
x_2_ary.append(x_2)
theta_ary=np.ones(len(t_ary))*theta
return t_ary,x_1_ary,x_2_ary,theta_ary
n=1000
X=[]
Y=[]
Y_2=[]
Y_3=[]
Z=[]
for i in range(n):
theta=2*np.pi/n*i
t_ary,x_1_ary,x_2_ary,theta_ary=simu(theta)
X.append(t_ary)
Y.append(x_1_ary)
Y_2.append(x_2_ary)
Y_3.append(theta_ary)
plt.xlabel("x_1")
plt.ylabel("x_2")
plt.contourf(Y,Y_2,Y_3,level=10,cmap="jet")
plt.colorbar(label="theta_0")
plt.savefig("安定性と位置.png")
plt.show()
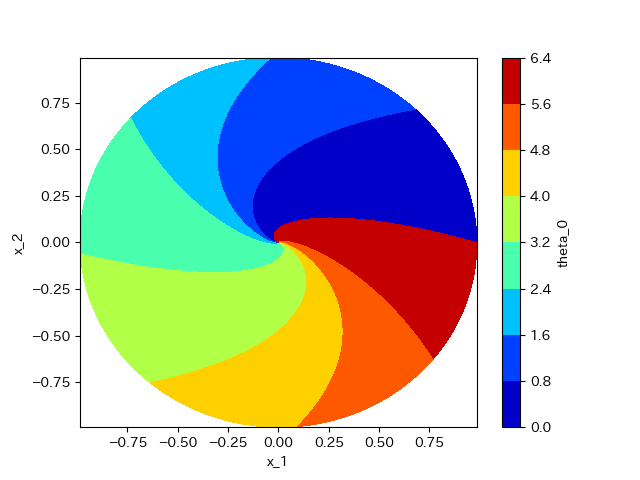
結果としては以下のグラフのようになる。
このように、ある程度カーブをしながら原点に収束していくようである。
まとめ
今回は、電験の現代制御の問題をモデルとして、フィードバック制御における位置の応答の様子をみた。現代制御は、古典制御とは異なり複雑な計算であるラプラス変換を行わなくてよいので、数値解析に適していると感じた。また、安定性についても理解し易い図をPythonで描写することができたので、勉強になった。次回は、PID制御も再現してみたい。