Go to Qiita Advent Calendar 2024 Top
LoginSignup
1
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@arairuca(達寛 新井)

2,3体問題と数値解析

Last updated at Posted at 2024-08-21

はじめに

複数の惑星が存在した場合、その惑星が万有引力によりどのような軌跡を描くのかを調査する問題を多体問題という。一般的に3体問題以上の系は厳密に数式を用いて運動方程式を解くことができない。そこで、今回は2体問題や3体問題についてpythonを用いた差分法で運動方程式を解くことにより、適切な計算量以内の範囲でシミュレーションをすることを目的とする。最後に3体問題について本記事で扱った差分法よりも近似精度が上がるルンゲ・クッタ法を用いることによっても上手く描写することができるかも調査する。

アルゴリズム

加速度と変位の関係式である運動方程式から変位を求めるために、以下のようなアルゴリズムを用いる。

速度と変位

微小区間($t=t$から$t=t+\Delta t$)に粒子の加速度$\textbf{a}$が与えられたとき
速度と変位は以下のように表すことができる。これは、微分の定義から来ている。

\textbf{v}(t+\Delta t)=\textbf{v}(t)+\textbf{a}(t)\Delta t

\textbf{x}(t+\Delta t)=\textbf{x}(t)+\textbf{v}(t)\Delta t

これを$t=0$から$t=t$まで加算することで$t=t$での位置$\textbf{x}(t)$を求めることができる。

説明

このアルゴリズムは差分法と呼ばれ、微分方程式を数値解析的に解くのに最も簡単な方法である。したがって、精度は粗くなってしまうので、$\delta t$を如何に小さくするかに懸かっている。しかし、それを行うと計算量が膨大になってしまうことから、上手くバランスを取ることがシミュレーションを適切に行う上で求められる。

2体問題

導入

以下のように、A,Bという惑星のみが存在する系を考える。
image.png

運動方程式

万有引力定数を$k$とすると運動方程式は以下のように表すことができる。


\begin{equation}
\left\{ \,
    \begin{aligned}
    & m_a \overrightarrow{a_a} = k\frac{m_a m_b}{|\overrightarrow{AB}|^2} \frac{\overrightarrow{AB}}{|\overrightarrow{AB}|} \\
    & m_b \overrightarrow{a_b} = k\frac{m_b m_a}{|\overrightarrow{BA}|^2} \frac{\overrightarrow{BA}}{|\overrightarrow{BA}|} \\
    \end{aligned}
\right.
\end{equation}

つまり、加速度と変位の関係は以下のようになる。


\begin{equation}
\left\{ \,
    \begin{aligned}
    &  \overrightarrow{a_a} = k\frac{ m_b}{|\overrightarrow{AB}|^2} \frac{\overrightarrow{AB}}{|\overrightarrow{AB}|} \\
    &  \overrightarrow{a_b} = k\frac{ m_a}{|\overrightarrow{BA}|^2} \frac{\overrightarrow{BA}}{|\overrightarrow{BA}|} \\
    \end{aligned}
\right.
\end{equation}

プログラム

上記の運動方程式に留意してプログラムを書くと以下のようになる。

2body-problem.py
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import japanize_matplotlib
#パラメータ
m_a=3
m_b=4
# 万有引力定数
k=1
# 初期条件
## 変位
x_a=0
x_b=1
## 速度
v_a=1j
v_b=-1j
## 加速度
a_a=0
a_b=0


# アニメを作る初期設定
fig = plt.figure()

ims = []


#初期時間
t=0
#微小時間の時間間隔(小さくするほど精度は上がるが計算時間が比例して増大する)
delta_t=0.1
while(t<30):
  im=[]
  #速度の微小変化
  v_a=v_a+a_a*delta_t
  #位置の微小変化
  x_a=x_a+v_a*delta_t

  #速度の微小変化
  v_b=v_b+a_b*delta_t
  #位置の微小変化
  x_b=x_b+v_b*delta_t

  a_a= (k*m_b/(abs(x_b-x_a))**3)*(x_b-x_a)
  a_b= (k*m_a/(abs(x_a-x_b))**3)*(x_a-x_b)
  
  im=plt.plot(x_a.real,x_a.imag,marker='o',color="red")
  im1=plt.plot(x_b.real,x_b.imag,marker='o',color="blue")
  
  ims.append(im+im1)
  #時間の更新
  t=t+delta_t
 
# 複数枚のプロットを 20ms ごとに表示
ani = animation.ArtistAnimation(fig, ims, interval=20)
#保存
ani.save("sample_2tai.gif", writer="pillow")

これを実行すると以下のようなgifファイルが生成される。

sample_2tai.gif

考察

上記のシミュレーション結果により、2つの天体は楕円運動をすることが分かる。これは、ケプラーの法則から上手く適切な計算精度でシミュレーションを行えているということを示唆している。ただし、天体があまりにも近づき過ぎると、位置エネルギーが発散してしまうため、力が無限大になり、加速度が無限大になり計算精度が悪化してしまうと考えられる。これは、後に述べる3体問題の計算精度がこの方法では悪くなってしまう原因であると考えられる。

3体問題

導入

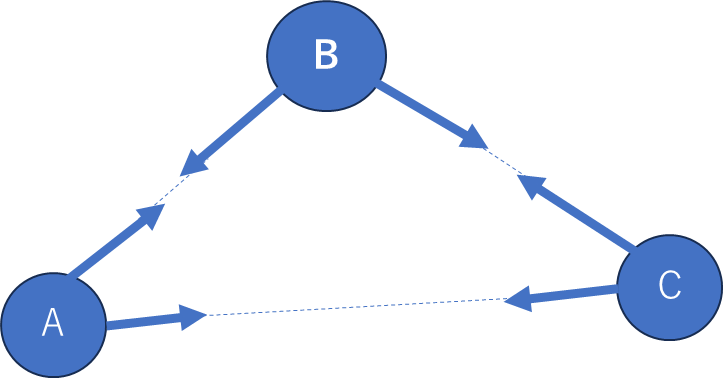
以下のように、A,B,Cという惑星のみが存在する系を考える。

image.png

運動方程式

万有引力定数を$k$とすると運動方程式は以下のように表すことができる。


\begin{equation}
\left\{ \,
    \begin{aligned}
    & m_a \overrightarrow{a_a} = k\frac{m_a m_b}{|\overrightarrow{AB}|^2} \frac{\overrightarrow{AB}}{|\overrightarrow{AB}|} +k\frac{m_a m_c}{|\overrightarrow{AC}|^2} \frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}\\
    & m_b \overrightarrow{a_b} = k\frac{m_b m_a}{|\overrightarrow{BA}|^2} \frac{\overrightarrow{BA}}{|\overrightarrow{BA}|} +k\frac{m_b m_c}{|\overrightarrow{BC}|^2} \frac{\overrightarrow{BC}}{|\overrightarrow{BC}|}\\
    & m_c \overrightarrow{a_c} = k\frac{m_c m_a}{|\overrightarrow{CA}|^2} \frac{\overrightarrow{CA}}{|\overrightarrow{CA}|} +k\frac{m_c m_b}{|\overrightarrow{CB}|^2} \frac{\overrightarrow{CB}}{|\overrightarrow{CB}|}\\
    \end{aligned}
\right.
\end{equation}

つまり、加速度と変位の関係は以下のようになる。


\begin{equation}
\left\{ \,
    \begin{aligned}
    & \overrightarrow{a_a} = k\frac{ m_b}{|\overrightarrow{AB}|^2} \frac{\overrightarrow{AB}}{|\overrightarrow{AB}|} +k\frac{ m_c}{|\overrightarrow{AC}|^2} \frac{\overrightarrow{AC}}{|\overrightarrow{AC}|}\\
    & \overrightarrow{a_b} = k\frac{ m_a}{|\overrightarrow{BA}|^2} \frac{\overrightarrow{BA}}{|\overrightarrow{BA}|} +k\frac{ m_c}{|\overrightarrow{BC}|^2} \frac{\overrightarrow{BC}}{|\overrightarrow{BC}|}\\
    &  \overrightarrow{a_c} = k\frac{ m_a}{|\overrightarrow{CA}|^2} \frac{\overrightarrow{CA}}{|\overrightarrow{CA}|} +k\frac{ m_b}{|\overrightarrow{CB}|^2} \frac{\overrightarrow{CB}}{|\overrightarrow{CB}|}\\
    \end{aligned}
\right.
\end{equation}

プログラム

上記の運動方程式に留意してプログラムを書くと以下のようになる。

3body-problem.py
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import japanize_matplotlib
#パラメータ
## 質量
m_a=1
m_b=1
m_c=1
# 万有引力定数
k=1
# 初期条件
## 変位
x_a=0
x_b=1
x_c=0.5+(0.5*3**0.5*1j)
## 速度
v_a=1j
v_b=-1j
v_c=-1
## 加速度
a_a=0
a_b=0
a_c=0

# アニメを作る初期設定
fig = plt.figure()

ims = []


#初期時間
t=0
#微小時間の時間間隔(小さくするほど精度は上がるが計算時間が比例して増大する)
delta_t=0.001
while(t<0.8):
  im=[]
  #速度の微小変化
  v_a=v_a+a_a*delta_t
  #位置の微小変化
  x_a=x_a+v_a*delta_t

  #速度の微小変化
  v_b=v_b+a_b*delta_t
  #位置の微小変化
  x_b=x_b+v_b*delta_t

  #速度の微小変化
  v_c=v_c+a_c*delta_t
  #位置の微小変化
  x_c=x_c+v_c*delta_t

  a_a= (k*m_b/(abs(x_b-x_a))**3)*(x_b-x_a)+(k*m_c/(abs(x_c-x_a))**3)*(x_c-x_a)
  a_b= (k*m_c/(abs(x_c-x_b))**3)*(x_c-x_b)+(k*m_a/(abs(x_a-x_b))**3)*(x_a-x_b)
  a_c= (k*m_a/(abs(x_a-x_c))**3)*(x_a-x_c)+(k*m_b/(abs(x_b-x_c))**3)*(x_b-x_c)

  im=plt.plot(x_a.real,x_a.imag,marker='o',color="red")
  im1=plt.plot(x_b.real,x_b.imag,marker='o',color="blue")
  im2=plt.plot(x_c.real,x_c.imag,marker='o',color="black")

  ims.append(im+im1+im2)
  #時間の更新
  t=t+delta_t
 
# 複数枚のプロットを 100ms ごとに表示
ani = animation.ArtistAnimation(fig, ims, interval=20)
#保存
ani.save("sample_3tai3.gif", writer="pillow")

これを実行すると以下のようなgifファイルが生成される。

sample_3tai3.gif

考察

3体問題の場合、特に惑星同士が接近する場合において高い計算精度がもとめられる。したがって、今回のシミュレーションでは、あえて短時間の範囲で行った。なので、長時間のシミュレーションを行う場合は、より精度が高い微分方程式を解くための数値解析手法を用いるべきであろう。

ルンゲ・クッタ法

ルンゲ・クッタ法とは、微分方程式を積算する数値解析法の一種で計算量と計算精度をバランス良く追求できる方法である。

以下の記事を参考に、本記事では4次のルンゲ・クッタ法を用いて数値解析を行うものとする。

python 3body-problem2.py
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import japanize_matplotlib


#パラメータ
## 質量
m_a=1
m_b=1
m_c=1
# 万有引力定数
k=1
# 初期条件
## 変位
x_a=0
x_b=1
x_c=0.5+(0.5*3**0.5*1j)
## 速度
v_a=1j
v_b=-1j
v_c=-1
## 加速度
a_a=0
a_b=0
a_c=0

# アニメを作る初期設定
fig = plt.figure()

ims = []


#微小時間の時間間隔(小さくするほど精度は上がるが計算時間が比例して増大する)
delta_t=1.0*10**-3


def F1_a(x_a,x_b,x_c,v_a,v_b,v_c, t):
    return v_a
def F2_a(x_a,x_b,x_c,v_a,v_b,v_c, t):
    return (k*m_b/(abs(x_b-x_a))**3)*(x_b-x_a)+(k*m_c/(abs(x_c-x_a))**3)*(x_c-x_a)
def F1_b(x_a,x_b,x_c,v_a,v_b,v_c, t):
    return v_b
def F2_b(x_a,x_b,x_c,v_a,v_b,v_c, t):
    return (k*m_c/(abs(x_c-x_b))**3)*(x_c-x_b)+(k*m_a/(abs(x_a-x_b))**3)*(x_a-x_b)
def F1_c(x_a,x_b,x_c,v_a,v_b,v_c, t):
    return v_c
def F2_c(x_a,x_b,x_c,v_a,v_b,v_c, t):
    return (k*m_a/(abs(x_a-x_c))**3)*(x_a-x_c)+(k*m_b/(abs(x_b-x_c))**3)*(x_b-x_c)



t=0
while(t<1):
  im=[]

  #print(x_b,x_c)
  #Runge-Kutta法(a)
  k1_a = delta_t*F1_a(x_a,x_b,x_c,v_a,v_b,v_c, t)
  m1_a = delta_t*F2_a(x_a,x_b,x_c,v_a,v_b,v_c, t)
  #k2 = delta_t*F1_a(x+0.5*k1, v+0.5*m1, t+0.5*delta_t)
  k2_a = delta_t*F1_a(x_a+0.5*k1_a,x_b,x_c,v_a+0.5*m1_a,v_b,v_c, t+0.5*delta_t)
  m2_a = delta_t*F2_a(x_a+0.5*k1_a,x_b,x_c,v_a+0.5*m1_a,v_b,v_c, t+0.5*delta_t)
  k3_a = delta_t*F1_a(x_a+0.5*k2_a,x_b,x_c,v_a+0.5*m2_a,v_b,v_c, t+0.5*delta_t)
  m3_a = delta_t*F2_a(x_a+0.5*k2_a,x_b,x_c,v_a+0.5*m2_a,v_b,v_c, t+0.5*delta_t)
  k4_a = delta_t*F1_a(x_a+k3_a,x_b,x_c,v_a+m3_a,v_b,v_c, t+delta_t)
  m4_a = delta_t*F2_a(x_a+k3_a,x_b,x_c,v_a+m3_a,v_b,v_c, t+delta_t)
  x_a = x_a + (k1_a + 2*k2_a + 2*k3_a + k4_a)/6
  v_a = v_a + (m1_a + 2*m2_a + 2*m3_a + m4_a)/6

  #Runge-Kutta法(b)
  k1_b = delta_t*F1_b(x_a,x_b,x_c,v_a,v_b,v_c, t)
  m1_b = delta_t*F2_b(x_a,x_b,x_c,v_a,v_b,v_c, t)
  #k2 = delta_t*F1_a(x+0.5*k1, v+0.5*m1, t+0.5*delta_t)
  k2_b = delta_t*F1_b(x_a,x_b+0.5*k1_b,x_c,v_a,v_b+0.5*m1_b,v_c, t+0.5*delta_t)
  m2_b = delta_t*F2_b(x_a,x_b+0.5*k1_b,x_c,v_a,v_b+0.5*m1_b,v_c, t+0.5*delta_t)
  k3_b = delta_t*F1_b(x_a,x_b+0.5*k2_b,x_c,v_a,v_b+0.5*m2_b,v_c, t+0.5*delta_t)
  m3_b = delta_t*F2_b(x_a+0.5*k2_b,x_b,x_c,v_a+0.5*m2_b,v_b,v_c, t+0.5*delta_t)
  k4_b = delta_t*F1_b(x_a,x_b+k3_b,x_c,v_a,v_b+m3_b,v_c, t+0.5*delta_t)
  m4_b = delta_t*F2_b(x_a,x_b+k3_b,x_c,v_a,v_b+m3_b,v_c, t+0.5*delta_t)
  x_b = x_b + (k1_b + 2*k2_b + 2*k3_b + k4_b)/6
  v_b = v_b + (m1_b + 2*m2_b + 2*m3_b + m4_b)/6


  #Runge-Kutta法(c)
  k1_c = delta_t*F1_c(x_a,x_b,x_c,v_a,v_b,v_c, t)
  m1_c = delta_t*F2_c(x_a,x_b,x_c,v_a,v_b,v_c, t)
  #k2 = delta_t*F1_a(x+0.5*k1, v+0.5*m1, t+0.5*delta_t)
  k2_c = delta_t*F1_c(x_a,x_b,x_c+0.5*k1_c,v_a,v_b,v_c+0.5*m1_c, t+0.5*delta_t)
  m2_c = delta_t*F2_c(x_a,x_b,x_c+0.5*k1_c,v_a,v_b,v_c+0.5*m1_c, t+0.5*delta_t)
  k3_c = delta_t*F1_c(x_a,x_b,x_c+0.5*k2_c,v_a,v_b,v_c+0.5*m2_c, t+0.5*delta_t)
  m3_c = delta_t*F2_c(x_a,x_b,x_c+0.5*k2_c,v_a,v_b,v_c+0.5*m2_c, t+0.5*delta_t)
  k4_c = delta_t*F1_c(x_a,x_b,x_c+k3_c,v_a,v_b,v_c+m3_c, t+0.5*delta_t)
  m4_c = delta_t*F2_c(x_a,x_b,x_c+k3_c,v_a,v_b,v_c+m3_c, t+0.5*delta_t)
  x_c = x_c + (k1_c + 2*k2_c + 2*k3_c + k4_c)/6
  v_c = v_c + (m1_c + 2*m2_c + 2*m3_c + m4_c)/6


  im=plt.plot(x_a.real,x_a.imag,marker='o',color="red")
  im1=plt.plot(x_b.real,x_b.imag,marker='o',color="blue")
  im2=plt.plot(x_c.real,x_c.imag,marker='o',color="black")

  ims.append(im+im1+im2)
  #時間の更新
  t=t+delta_t
 
# 複数枚のプロットを 2ms ごとに表示
ani = animation.ArtistAnimation(fig, ims, interval=2)
#保存
ani.save("sample_3tai3_ran3.gif", writer="pillow")

これを実行すると以下のようになる。

sample_3tai3_ran8_10.gif

ルンゲ・クッタ法を用いても簡易的な差分法とあまり差が見られなかった。従って、3体問題を扱うときは、物体が近くなったときのみ時間の粒度を細かくするといった手法を持ちた方がよいようである。

まとめ

今回は、差分法を用いた数値解析手法を用いて、2体問題や3体問題をシミュレーションすることを目的とした。結果、2体問題では、惑星は楕円運動をした。一方で3体問題では複雑な運動をした。ただし、今回のような問題は高い精度と膨大な計算量が必要になるので、アルゴリズムや性能の高い計算機を使うことが、より良い精度のシミュレーションを行うには必要であると考えられる。

1
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?