はじめに
摩擦のない斜面を転がる物体には2種類の力が働く。重力と垂直抗力である。つまり、その2つの力の向きと大きささえ決定されれば運動方程式を立式することができる。一方で、微分の考え方は滑らかな曲面における微小区間は直線に近似することができるというものである。そこで今回は、まず、直線斜面上を転がる物体の運動をプログラミングを用いてシミュレーションした後に、円形の斜面上を転がる物体の運動について調査する。具体的には、シミュレーションが高校の力学で習う円運動の運動方程式から導かれる結論を満たすことを確かめる。
1.直線斜面を転がる物体の運動
このように斜面を加速しながら降下していく。
2.円形の斜面上を転がる物体の運動
このように、ある位置までは斜面上を転がっていたが、それ以降だと斜面から離れて、放物線運動をする。
導入
直線斜面
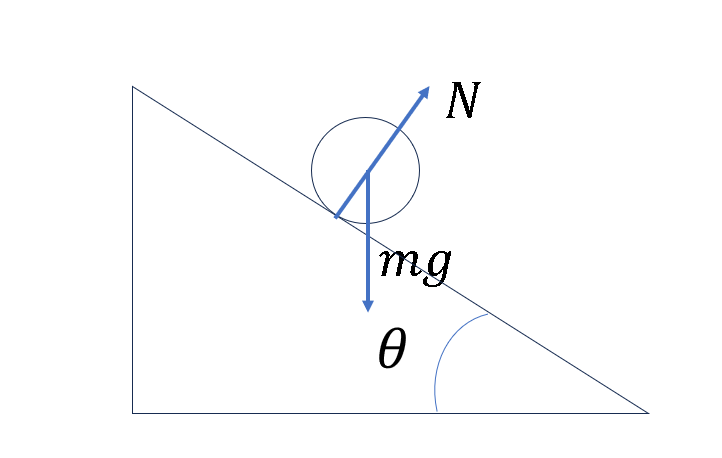
以下のような、直線斜面を転がる物体の運動方程式を考える。
斜面方向のつり合いより、垂直抗力$N$は以下のような式を満たす。
N=mg cos \theta
したがって、水平方向の運動方程式は以下のように表すことができる。
m \frac{d^2x}{dt^2}=N sin\theta
一方で、鉛直方向の運動方程式は以下のように表すことができる。
m \frac{d^2y}{dt^2}=N cos\theta -mg
滑らかな斜面
ここで、斜面の曲線の方程式を$y=g(x)$とする。このとき、位置$x$における傾きは微分を用いて、
\frac{dy}{dx}=\frac{dg(x)}{dx}=-tan\theta
と表すことができる。ただし、$\theta$は水平線とのなす角である。
したがって、
\theta=-tan^{-1}(\frac{dg(x)}{dx})
この式を、直線斜面の質点の運動方程式に代入することで、滑らかな曲線斜面の運動方程式を立式することができる。
直線斜面
以下のようなプログラムを作成した。
プログラム
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import japanize_matplotlib
# アニメを作る初期設定
fig = plt.figure()
ims = []
plt.xlim(0, 1)
plt.ylim(0, 1)
m=1
g=9.8
L=1
def f(x0):
## 円
#return (1-x0**2)**0.5 #円
## 直線
return 1-x0
#斜面の描写
xx_ary = np.linspace(0, L, 100)
yy_ary= f(xx_ary)
t=0
delta_t=0.003
delta_xx=0.001
#初期位置
x=0.1
y=f(x)
#初速度
v_x=0
v_y=0
while(t<1.5):
im=[]
if y<=f(x):
if x+delta_xx>L:
F_x=0
F_y=-m*g
else:
delta_yy=f(x+delta_xx)-f(x)
delta_y=-delta_yy/delta_xx
N= m*g*np.cos(np.arctan(delta_y))
F_x=N* np.sin(np.arctan(delta_y))
F_y=-m*g+N*np.cos(np.arctan(delta_y))
else:
F_x=0
F_y=-m*g
im1=plt.plot(xx_ary,yy_ary,color="blue")
#質点の描写
im2=plt.plot(x,y,"o",color="red")
#im3=plt.plot(3**0.5/2,1/2,"o",color="black")
#ims.append(im1+im2+im3)
ims.append(im1+im2)
a_x=F_x/m
a_y=F_y/m
v_x=v_x+a_x*delta_t
v_y=v_y+a_y*delta_t
x=x+v_x*delta_t
y=y+v_y*delta_t
t=t+delta_t
# 複数枚のプロットを 20ms ごとに表示
ani = animation.ArtistAnimation(fig, ims, interval=20)
#保存
ani.save("直線斜面を転がる物体.gif", writer="pillow")
円形斜面
問題設定
以下のような、円形の斜面を転がる質点を考える。
初速度を与えずに、頂点から転がす。このとき、ある位置において物体が斜面から離れる。その位置を求めたい。
代数解析
そこで、手計算による解析を行う。具体的には、向心力を用いた運動方程式とエネルギー保存の法則を連立させて、垂直抗力が0となる点を求める。円形斜面上の質点の座標を$(rcos\theta,rsin\theta)$とおく。
向心力つまり、中心方向の運動方程式は以下のように表すことができる。
運動方程式
m\frac{v^2}{r}=mg sin\theta-N
エネルギー保存の法則
一方でエネルギー保存の式は以下のようになる。
\frac{1}{2}mv^2+ mg rsin\theta=mgr
この2式を連立させ、$N=0$とすると、
sin \theta = \frac{r}{1+r}
となる。ここで、$r=1$とすれば、$(\frac{\sqrt{3}}{2},\frac{1}{2})$の座標に質点がきたとき質点は斜面から離れ宙に浮かぶ。これをシミュレーションする。
プログラム
以下のようなプログラムを作成した。
import numpy as np
import matplotlib.pyplot as plt
import matplotlib.animation as animation
import japanize_matplotlib
# アニメを作る初期設定
fig = plt.figure()
ims = []
plt.xlim(0, 1)
plt.ylim(0, 1)
m=1
g=9.8
L=1
def f(x0):
## 円
return (1-x0**2)**0.5 #円
## 直線
#return 1-x0
#斜面の描写
xx_ary = np.linspace(0, L, 100)
yy_ary= f(xx_ary)
t=0
delta_t=0.003
delta_xx=0.001
#初期位置
x=0.1
y=f(x)
#初速度
v_x=0
v_y=0
while(t<1.5):
im=[]
if y<=f(x):
if x+delta_xx>L:
F_x=0
F_y=-m*g
else:
delta_yy=f(x+delta_xx)-f(x)
delta_y=-delta_yy/delta_xx
N= m*g*np.cos(np.arctan(delta_y))
F_x=N* np.sin(np.arctan(delta_y))
F_y=-m*g+N*np.cos(np.arctan(delta_y))
else:
F_x=0
F_y=-m*g
im1=plt.plot(xx_ary,yy_ary,color="blue")
#質点の描写
im2=plt.plot(x,y,"o",color="red")
im3=plt.plot(3**0.5/2,1/2,"o",color="black")
ims.append(im1+im2+im3)
a_x=F_x/m
a_y=F_y/m
v_x=v_x+a_x*delta_t
v_y=v_y+a_y*delta_t
x=x+v_x*delta_t
y=y+v_y*delta_t
t=t+delta_t
# 複数枚のプロットを 20ms ごとに表示
ani = animation.ArtistAnimation(fig, ims, interval=20)
#保存
ani.save("円形斜面を転がる物体.gif", writer="pillow")
この動画を見てわかるとおり、$(\frac{\sqrt{3}}{2},\frac{1}{2})$の点に質点が到達したときに、斜面から離れる。
まとめ
今回は、高校の力学の復習として斜面を転がる物体の運動について考察した。斜面が直線か曲線かによって垂直抗力が異なるので、運動の特徴も異なるということが分かった。また、微分方程式を解くために用いた数値解析手法、オイラー法はある程度の誤差を容認すれば、実用的であるということも分かった。