生年月日からシンプルに年齢を算出する数式とその証明
※記事内の数式の図が表示されるまで1分ぐらい掛かることがあります
計算式
誕生日から年齢を簡易的に求めたいとき、
yyyymmdd形式で表記した今日の日付から、同じくyyyymmdd形式で表記した誕生日をそのまま引き算し、10,000で割った解の整数部分を現時点での年齢とすることができる。
例えば、本日が2017/08/18で、誕生日が1990/08/20 なら、
\begin{align}
\mbox{年齢}
&=floor\left(\frac{20170818-19900820}{10000}\right)\\
&=floor\left(\frac{269998}{10000}\right)\\
&=floor\left(26.9998\right)\\
&=26
\end{align}
※$floor$は小数部分を切り捨てる処理
これを一般化すると以下の数式になる。
\begin{align}
\mbox{年齢}
&=floor\left(\frac{\left(\mbox{現在年}\times10000+\mbox{現在月}\times100+\mbox{現在日}\right)-\left(\mbox{誕生年}\times10000+\mbox{誕生月}\times100+\mbox{誕生日}\right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }{10000}\right)
\end{align}
計算例
本日が2017/08/18で、誕生日が1990/08/20 なら、
\begin{align}
\text{年齢}
&= floor\left(\frac{\left(2017\times1000+08\times100+18\right)-\left(1990\times1000+08\times100+20\right)}{10000}\right)\\
&= floor\left(\frac{20170818-19900820}{10000}\right)\\
&= floor\left(\frac{269998}{10000}\right)\\
&= floor\left(26.9998\right)\\
&= 26
\end{align}
本日が2017/08/20で、誕生日が1990/08/20なら、
\begin{align}
\text{年齢}
&= floor\left(\frac{\left(2017\times1000+08\times100+20\right)-\left(1990\times1000+08\times100+20\right)}{10000}\right)\\
&=floor\left(\frac{20170820-19900820}{10000}\right)\\
&=floor\left(\frac{270000}{10000}\right)\\
&=floor\left(27\right)\\
&=27
\end{align}
つい脊髄反射で「UNIXタイムからの経過ミリ秒に直して…」の様にやりたくなるが、冷静に考えるとこのロジックこそ とても自然な発想だと思う。
(イマイチ納得できない方向けにこちらでもう少し分かりやすく解説)
但し、年齢計算の式は(特に法律関係で)利用対象によって定義が変わることがあるため、この計算式をそのまま使えるとは限らない。
コード
JavaScriptのとき
/**
* 誕生日から年齢を返す関数
* @param {!string} birthdayStr - 誕生日をyyyymmdd形式で入力
* @return {number} 計算された年齢
**/
var calcAge = function(birthdayStr){
if(isNaN(birthdayStr)||birthdayStr.length !== 8){
return -1;
}
var d = new Date();
var dStr = ''+d.getFullYear()+('0'+(d.getMonth()+1)).slice(-2)+('0'+d.getDate()).slice(-2);
return Math.floor((parseInt(dStr)-parseInt(birthdayStr))/10000);
};
console.log(calcAge('19900820'));
Python 3.Xのとき
# -*- coding: utf-8 -*-
from datetime import datetime
import math
def calcAge(birthdayStr):
if not (birthdayStr.isdigit() and len(birthdayStr)==8):
return -1
dStr = datetime.now().strftime("%Y%m%d")
return math.floor((int(dStr)-int(birthdayStr))/10000)
print(calcAge("19900817"))
returnの式は
return (int(dStr)-int(birthdayStr))//10000
でもOK。
Rubyのとき
require "date"
def calcAge(birthdayStr)
if birthdayStr !~ /^[0-9]{8}$/
return -1
end
return (Date.today.strftime("%Y%m%d").to_i - birthdayStr.to_i) / 10000
end
print calcAge("19900820")
Rubyでは整数型同士の除算で小数点以下が勝手に切り捨てられるためfloor処理が不要。
SQLのとき
→ SQL日付関数(年齢計算) | dbSheetClient IT技術ブログ
PHP、Java、Perlのとき
→ 佐野裕のサーバ管理者日記 - 生年月日から年齢を計算する簡単な計算式:ITpro
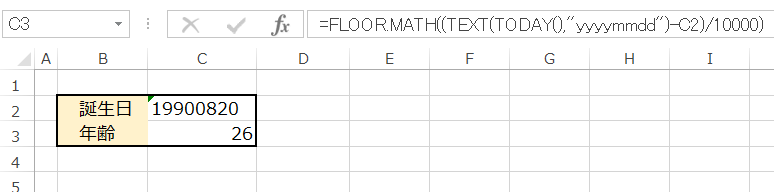
Excelのとき
DATEDIF()関数があるのでこの数式は不要だが、CSVを取り込んで処理するときに元データが日付型になっていないときには有効な手段。
=FLOOR.MATH((TEXT(TODAY(),"yyyymmdd")-[yyyymmdd形式の生年月日])/10000)
FLOOR.MATH()関数は古いExcelでは使えない。そのときはINT関数を使えばOK。
=INT((TEXT(TODAY(),"yyyymmdd")-[yyyymmdd形式の生年月日])/10000)
小話 - 年をとる瞬間
この数式では現時点での年齢を算出しているが、今日何歳になるかを算出している訳ではない。
年齢計算ニ関スル法律によると、加齢するタイミングは誕生日当日ではなく、誕生日の前日を満了する瞬間(=前日24時0分0秒)とのこと。
即ち、2000年4月1日生まれの人は2006年3月31日が始まった時点では5歳であるが、3月31日中に満6歳になり、既に満6歳になった状態で2006年4月1日を迎える。
この定義により、うるう年2月29日生まれの人でも毎年1歳ずつ加齢する。
誕生日と学年について
学校教育法によると、4月1日の前日までに満6歳となっている人は、小学校へ入学することとなっている。
「2000年4月1日生まれの人」は2006年4月1日の前日である2006年3月31日には満6歳になっているので、2006年4月1日より小学1年生になる。同様の理由で「2000年3月15日生まれの人」、「1999年4月20日生まれの人」も同じ学年である。
「2000年4月2日生まれの人」は2006年4月1日の前日には満6歳に達していないため、翌年の2007年4月1日より小学1年生になる。
数式のやや詳しい解説
もう少し掘り下げて考えたい方向け。
誕生年と現在の年だけの情報でも、「今年で何歳になるか」までは分かる。
今年の年齢 = 現在年 - 誕生年
だが、今年の誕生日を迎えたか分からないので「今の年齢」が分からない。
もし、今年の誕生日を迎えていないのであれば、「今の年齢」は「今年の年齢」から$1$を引いて計算する必要がある。
これを場合分けの式で表現すると以下のようになる。
\begin{eqnarray}
\mbox{年齢}=\left\{
\begin{array}{ll}
\mbox{現在年}-\mbox{誕生年}&\left(\mbox{誕生月日}\leq\mbox{現在月日}\right)\cdots\mbox{(1)今年の誕生日以降の式}\\
\mbox{現在年}-\mbox{誕生年}\color{red}{-1}&\left(\mbox{誕生月日}>\mbox{現在月日}\right)\cdots\mbox{(2)今年の誕生日前日までの式}\\
\end{array}
\right.
\end{eqnarray}
年齢の簡易計算式を変形すると、上記の場合分けの式と似た数式を作ることができる。
この変形後の数式の$\color{red}{赤文字部分}$に「今年の誕生日を迎えていないなら$-1$する」という処理が内包されている。
\begin{align}
\mbox{年齢}
&=floor\left(\frac{\left(\mbox{現在年}\times10000+\mbox{現在月}\times100+\mbox{現在日}\right)-\left(\mbox{誕生年}\times10000+\mbox{誕生月}\times100+\mbox{誕生日}\right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }{10000}\right)\\
&=floor\left(\frac{\left(\mbox{現在年}-\mbox{誕生年}\right)\times10000+\left(\mbox{現在月}-\mbox{誕生月}\right)\times100+\mbox{現在日}-\mbox{誕生日}\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }{10000} \right)\\
&=\color{red}{floor}\left(\mbox{現在年}-\mbox{誕生年}\color{red}{+\frac{\mbox{現在月}-\mbox{誕生月}}{100}+\frac{\mbox{現在日}-\mbox{誕生日}}{10000}}\right)\\
\end{align}
この式の月と日の計算結果の合計部分を$X$と置き換えると、先ほど登場した場合分けの式と良く似たシンプルな数式になる。
\begin{align}
\mbox{年齢}&=\color{red}{floor}\left(\mbox{現在年}-\mbox{誕生年}\color{red}{+X}\right)\\\\
\color{red}{X}&=\frac{\mbox{現在月}-\mbox{誕生月}}{100}+\frac{\mbox{現在日}-\mbox{誕生日}}{10000}\\\\\\
\end{align}
$X$の値が取りうる範囲については以下のとおり
- 本日が誕生日当日であるとき
→ 現在月=誕生月、現在日=誕生日なので$0$
- 本日が12月31日で、誕生日が1月1日のとき
→ 最大値$X_{max}$
\begin{align}
X_{max}&=\frac{\mbox{12}-\mbox{1}}{100}+\frac{\mbox{31}-\mbox{1}}{10000}=0.1130\\\\
\end{align}
- 本日が1月1日で誕生日が12月31日のとき
→ 最小値$X_{min}$
\begin{align}
X_{min}&=\frac{\mbox{1}-\mbox{12}}{100}+\frac{\mbox{1}-\mbox{31}}{10000}=-0.1130
\end{align}
よって
-0.1130\leq X \leq 0.1130
| 現在と年内の誕生日の関係 | $X$の取りうる値 |
|---|---|
| $\mbox{誕生月日}\leq\mbox{現在月日}$のとき(誕生日以降) | $0\leq X_{after}\leq0.1130$ |
| $\mbox{誕生月日}>\mbox{現在月日}$のとき(誕生日前日以前) | $-0.1130\leq X_{before}<0$ |
今年の誕生日当日以降の計算
「 $\mbox{現在年}-\mbox{誕生年}$ 」の結果は必ず$0$以上の整数になり、$0\leq X_{after}\leq0.1130$であるため、
$X$は計算結果に影響を与えず、無視される。
\begin{align}
\mbox{年齢}
&=floor\left(\mbox{現在年}-\mbox{誕生年}\color{red}{+X_{after}}\right)\\
&=\mbox{現在年}-\mbox{誕生年}
\end{align}
これは**場合分けの式「(1)今年の誕生日以降の式」**と一致する。
まだその年の誕生日を迎えていないときの計算
「 $\mbox{現在年}-\mbox{誕生年}$ 」の結果は必ず$0$以上の整数になり、$-0.1130\leq X_{before}<0$であるため、
$X$は年の計算結果から1を引く影響を与える。
\begin{align}
\mbox{年齢}
&=floor\left(\mbox{現在年}-\mbox{誕生年}\color{red}{+X_{before}}\right)\\
&=\mbox{現在年}-\mbox{誕生年}\color{red}{-1}
\end{align}
これは**場合分けの式「(2)今年の誕生日前日までの式」**と一致する。
よって、数式
\begin{align}
\mbox{年齢}
&=floor\left(\frac{\left(\mbox{現在年}\times10000+\mbox{現在月}\times100+\mbox{現在日}\right)-\left(\mbox{誕生年}\times10000+\mbox{誕生月}\times100+\mbox{誕生日}\right)\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ }{10000}\right)
\end{align}
の解は、以下の場合分けの式と同じ解となり、誕生日から現在の年齢を求めることができる。
\begin{eqnarray}
\mbox{年齢}=\left\{
\begin{array}{ll}
\mbox{現在年}-\mbox{誕生年}&\left(\mbox{誕生月日}\leq\mbox{現在月日}\right)\cdots\mbox{(1)今年の誕生日以降の式}\\
\mbox{現在年}-\mbox{誕生年}\color{red}{-1}&\left(\mbox{誕生月日}>\mbox{現在月日}\right)\cdots\mbox{(2)今年の誕生日前日までの式}\\
\end{array}
\right.
\end{eqnarray}
あとがき
プログラミングの面白さの1つとして、脳内で行っている処理を如何に具体化してシンプルなロジックに落とし込めるかというものがあります。
このコードにはその面白さがシンプルに詰まっているので、眺めているだけで楽しかったです。
Excelの日付処理に興味が湧いた方はこちらもどうぞ。
→ 【Excel】 日時情報の正体 - Qiita
yyyymmdd形式の検査をもっとしっかりやりたい方へ
→ yyyymmdd形式日付文字列の妥当性をチェックする正規表現を読み解く - Qiita