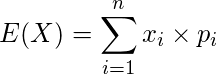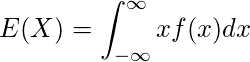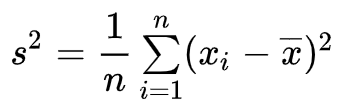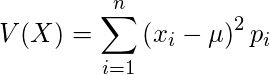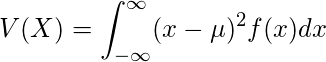BI技術者認定試験前に学んだ事をまとめてみた①

自己紹介

大学ではCell Biologyを専攻にしており、食品×医療の研究をしています。データサイエンス・機械学習に興味があり、東京大学松尾研究室で共同研究に参加したり、東京大学グローバル消費インテリジェンス寄附講座で講師をしたり、様々な経験をさせて頂いております。

はじめに

私事ですが、今夏に大学院試験を終えまして、そこで学んだ知識の復習をしながら何か新しいことを学べないだろうかと思っているとこのような資格に出会いました。

バイオインフォマティクス技術者認定試験

本認定試験は、合格者が基礎から先端までの基本知識を有し、関連業務への適性が一定レベルに達した人材であることを示せるよう作られています。 Society 5.0においてもバイオインフォマティクスは医療・ヘルスケアITと密接 に関連する重要技術であり、産業界では，バイオインフォマティクス関連業務の 入札や雇用で当該試験の合格が要件となっていたり、社員の育成を重視する企業 に利用されています。また、学生や一般の方がバイオインフォマティクスを勉強する際の指針となるように設計されており、リカレントを含む教育の入り口としても機能しています。当学会としては、国家資格化などによりこれらの効果を強化することが目標の一つです。現在、バイオインフォマティクススキル標準の策定も他学会と連携して進めています。

この試験を見つけた時は、「なんだこの試験」と思いましたが、調べていると、生命科学だけでなく、数学・情報学・バイオインフォマティクスを勉強する必要があり、院試の復習をしながら情報系学べて一石二鳥じゃんと思いました。試験は12月14日にあるので追い込み頑張ります！

【追記】バイオインフォマティクス技術者認定試験を合格してました。
全体正答率80%でした！過去３年間の合格基準が正答率56~58%だったので、まずまずですね。
出題分野ごとの正答率を見てみると、生命科学は100%だったのに対し、構造科学やオーミクスは50%とかなりばらつきがありました。Cell Biologyを専攻にしていて、ドライの知見は全然で甘くないですね。

第１章　生命科学

シークエンシング

シークエンシング(配列解読)は、本試験において最も出題されているキーワードの一つです. 個人的には、ここを理解しておくだけで点数がかなり安定するのかなと思います。

• 歴史は、サンガー法/マクサム-ギルバート法→自動化→次世代シークエンサの順.
• サンガー法は、ジデオキシヌクレオチドを利用してDNAポリメラーゼによるDNA鎖の伸長反応を配列特異的に停止し、生成された長さの異なるDNA断片を電気泳動によって分離・配列決定する方法である.
• 次世代シークエンサは、現在非常に複雑・多様化している。　従来と大きく変わったところは、断片かされたゲノム配列を解析する際にコンピュータが活用され、非常に高速化されたということ.
• 利用方法は、ゲノム配列のアセンブリ、新規のゲノム配列の解読、リシークエンス、多型検出、mRNAの発現解析、(選択的スプライシングなどで生み出された)新規mRNAのアセンブリ、エキソン領域の網羅的解析、転写因子などのDNAなどの結合タンパクが認識する配列の同定、メタゲノム解析などがあり、本当に様々な分野で活用されている。

タンパク質の立体構造解析

• ポイントは２つ. X線結晶解析法はX線を結晶に、NMRは電磁波を溶液試料に、電子顕微鏡は電子線を固定化資料に照射すること、そして電子顕微鏡は他の二つと併用して利用されることが多いことです.
• X線結晶解析法:タンパク質の結晶にX線を照射すると、X線の一部が散乱し、特定の方向のみに干渉し合う「回析」を観測することで、結晶中の電子の分布、さらには原子の配置を決定する方法. 「タンパク質を結晶化する」というところがボトルネック.
• 核磁気共鳴法(NMR法):核磁気共鳴を用いて分子の構造や運動状態などの性質を調べる方法. 「感度が低い=試料量が多く必要, 測定時間が長い」というところがボトルネック.
• 電子顕微鏡法：大きく分けると、「透過電子顕微鏡」と「走査電子顕微鏡」の２種類に分けられる.通常の顕微鏡の光源が可視光線なのに対し、電子顕微鏡では電子線を用いている.

第２章　計算科学

シフト演算の意味

• シフト演算とは、与えられた二進法のビットを左または右にnビットずらすことで乗除算を行うこと
• 普通に掛け算・割り算するよりも処理速度が速いから使われている
• 論理演算では、ド・モルガンの法則, 分配法則が利用されることが多い

コンピュータ

• CPU(Central processing unit)は制御部と演算部がある
• キャッシュメモリがあると操作が高速化する！毎回メモリとやりとりしなくていい。
  • タンス貯金みたいなイメージ, 毎回下ろすの面倒臭い
• キャッシュメモリは階層化されている。1次, 2次, 3次キャッシュ
• RAMとは、PCにおいて、CPUが直接アクセスして演算を実行するときに使うメインメモリ（主記憶装置）のこと. CPUが動作する時に一時的にデータを記憶しておく装置で、一般的に「メモリ」という言葉はこのRAMを指すことが多い
• RAMが多い方が高速で多くの並行演算処理ができる

プログラミング言語

• コンパイラ型, インタープリンタ型の言語

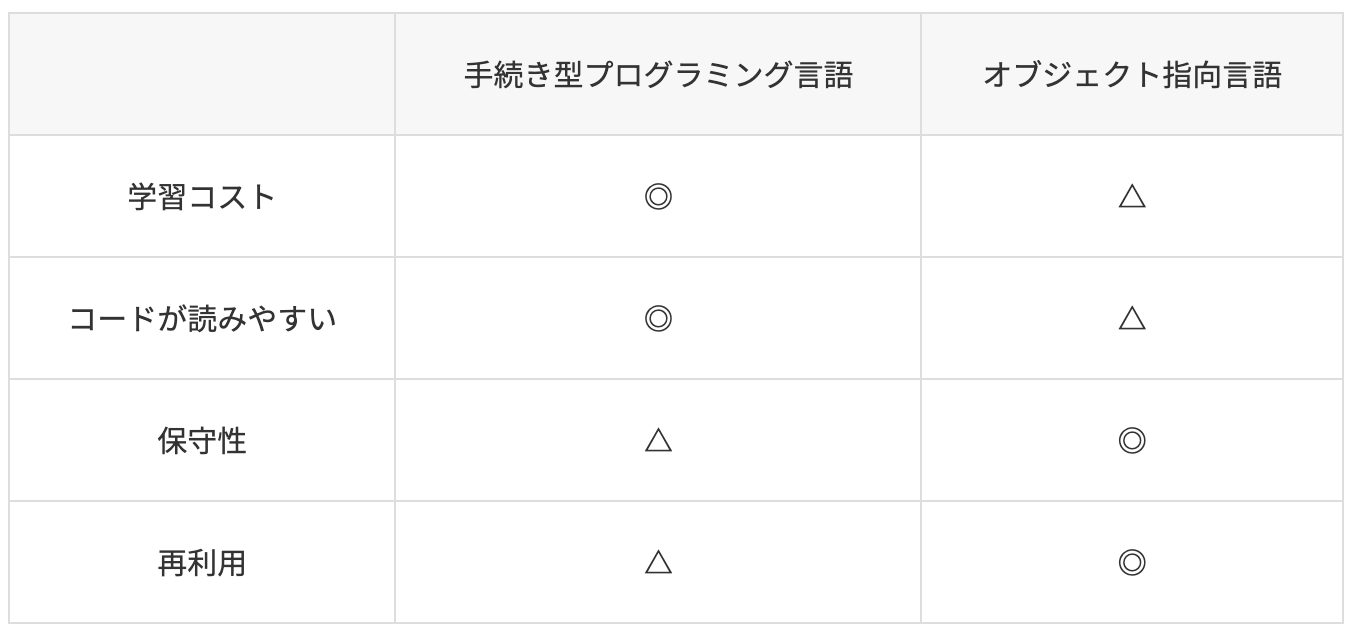
• 手続き型言語とオブジェクト指向言語

XML, HTML

• マークアップ言語(プログラミング言語とは異なる)
• 各要素をタグで囲み、階層的なデータ構造を入れ子で表現する
  • 文章中の文字列を修飾するだけでなく、文書の構造(見出しや段落)を指定する
• XMLでは、ユーザーが新たなタグを定義して言語を拡張することができる
  • タグの定義はDTDという書式によってXML中または別ファイルにて定義することができる
• データ構造の変更が容易で、RDBなどの他のデータ形式への変換も簡単である
• 画像や音声などの非構造データも文字列に変換して扱える

TCP/IP

• 通信プロトコル体系・概念の一つ
• TCP/IPは階層構造を持ち、Application, Transport, Internet, NetworkInterface層の四層からなる。それぞれの層で違った種類のプロトコル(約束事)があり、データの送受信の際に実行されている

IPアドレス・ポート

• IPアドレスは住所、ポート番号はマンションの部屋番号. IPアドレスとポート番号の組み合わせによって「どこにあるサーバにどのようなサービスを依頼する」かが一意に決まる.
  • IPアドレスとは、インターネット・プロトコル において、通信の相手先を識別するための番号である
    • プライベートipアドレス(重複OK)→これだけではネットに接続できない
    • グローバルipアドレス(重複NG)→これでネットに接続
  • ipアドレスだけではアプリケーションの種類を見分けることが出来ない. ポート番号を利用してアプリケーションを判別している.
    • サーバー側が固定、ユーザー側のポート番号は毎回変わる
    • http=80, https=443など

ネットワークとセキュリティ

• 公開鍵暗号を用いて暗号化するプロトコルとして
  • 遠隔ログイン：SSH
  • ファイル送信：SFTP
  • サーバー・ユーザー間通信：HTTPS
  • メールの送受信：SMTPS, POP3S

探索アルゴリズム

• 線形探索
  • しらみつぶし. 前から見ていって目的の値見つけるまで探す感じ
  • 平均比較回数がn/2, 最大はn回
• 二分探索
  • 配列の中間にある値をチェックし、探索対象がそれよりも「大きい」「小さい」などで切り分けていく
  • 大小関係が綺麗に整列されたデータのみ使える
  • データ数がn個なら, 平均比較回数がlog2 n回, 最悪はlog2(n+1)回.
  • ⇄ 操作n回で2^(n+1) - 1個の値を発見することが可能である.
• ハッシュ探索
  • まずは、ハッシュ表を作り、キーとそれに対応する値をペアで格納する.
  • ハッシュ関数により数値をハッシュ値に変換し、格納位置を決める.
  • ハッシュ衝突が無ければ、計算により一発で探索が終了する！

ソートアルゴリズム

【Unity】ソートアルゴリズム12種を可視化してみた - Qiita

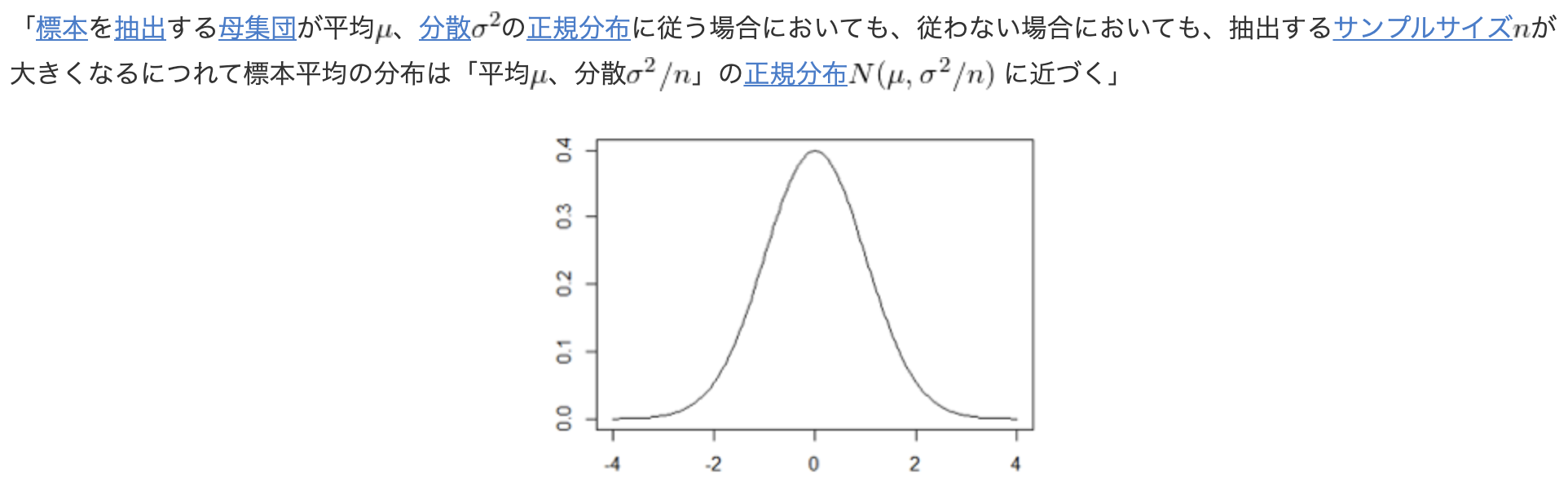
中心極限定理

確率分布

確率変数の期待値

• 確率変数の期待値は、確率変数がとる値とその値をとる確率の積を全て足し合わせたもので、確率変数の平均値を表す。
• 離散型確率変数(上式), 連続型確率変数(下式)の期待値

• 期待値の性質
  • E(C) = C
  • E(X+C)=E(X)+E(C)=E(X)+C
  • E(kX)=kE(X)
  • E(X+Y)=E(X)+E(Y) (X, Yが独立じゃなくても成り立つ。差も同様)
  • E(XY)=E(X)E(Y) (X, Yが独立ならば成り立つ

データの分散

• 分布のひろがりを表す統計量の一つで、標準偏差の2乗に等しい.

確率変数の分散

• 分散は、「確率変数のとり得る値と期待値（平均値）の差の2乗」と「確率」との積を、全て足し合わせたもの.
• 分散を計算することで、確率変数のとる値が期待値の周りにどの程度ばらついているかが分かる. 分散が小さいほど確率変数の取りうる値は期待値に集まっていることを表す.

• 分散の性質
  • V(C)=0
  • V(X+C)=V(X)
  • V(kX)=k^2・V(X)
  • V(X+Y)=V(X)+V(Y)+2Cov(X, Y)（XとYが独立でない場合。差も同様）
  • V(X+Y)=V(X)+V(Y)（XとYが独立=共分散0ならば成り立つ。差も同様）

確率と尤度

• 確率が未来に起こる出来事の予想であるのに対して、尤度は過去の状態の推定にあたる。ただし、実際の計算方法は確率と尤度は似通っており、特別な仮定の無い場合は同一である。
  • つまり、計算は一緒だけどスタンス(考え方)が違う

クラスタリング

• クラスタリングには階層型と非階層型がある.
  • 階層型はデータの類似度によって似たものを階層的にクラスタに分類していく. 結果として木構造が得られる.
  • 非階層型はクラス分類のみが行われる. 一般的にはk-means法が利用される.

参考文献

この記事は以下の情報を参考にして執筆しました。

• バイオインフォマティクス入門

※画像の著作権の詳しい確認が取れていません。確認が取れなかった場合は、即掲載を取り消します。