AHC030のseed0のvisualizer動画
X(旧twitter)などでAHC030の感想を見ていると、seed0で範囲取得を数回バババッてやっていきなりドンピシャで正解しているのを目にします。これは見た目やばいけど、じつは結構簡単に実装できるよというお話です。
↓私の最終提出のseed0です。costは0.37くらいらしい
ベイズ推定!
結論から言うと、ベイズ推定をしていきます。なんか難しそうな名前をしていますが、(今回のテーマを実現するだけなら)実はそんなに難しくないです。
ベイズの定理によると、$P(A)$を事前確率(その時点の情報から求まってる、事象$A$の確率)、$P(A|X)$を事後確率(事象$X$が確定したあとの事象Aの確率)とおくと、$P(A|X)$は$P(A)\times P(X|A)$に比例するらしいです。今回はこの定理を証明せず信じることにしますが、これは具体的にどういう意味なのでしょうか。
まず、$A$は盤面のことだと思ってください。そして$X$というのはクエリの結果だと考えましょう。そうすると、今回の問題はクエリを何回か投げた後に、答えが各盤面である確率を求めることだと考えることができます。(その上で、確率が十分に高いときは答えるということにしましょう。)
考えられる盤面の列を$B_1,\ B_2,\ ...\ ,\ B_n$、$i$番目のクエリの前の各盤面の確率を$P_{i,\ 1},\ P_{i,\ 2},\ ...\ ,\ P_{i,\ n}$と置くことにしましょう。
そうすると、$P_{1,\ 1} = P_{1,\ 2} =\ ...\ = P_{1,\ n} = 1/ n$であることが分かると思います。(入力生成方法のところに可能な盤面は全て等確率に選ばれると書いてあります)
$i$番目のクエリの答えをもとに列$P_i$を$P_{i+1}$に更新することを考えましょう。$i$番目のクエリの結果を$X_i$とおくとベイズの定理から、
P_{i+1,\ j} = P_{i,\ j} \times P(X_i|B_j)
というふうに更新できます。(規格化は一旦無視しています)
ここで、$P(X_i|B_j)$とは盤面$B_j$に対してクエリを打った時に結果が$X_i$となる確率を表しています。(尤度といいます)
今回は、盤面から出力を選ぶ際の分布が問題文に書いてあるので、それに則って正規分布の累積分布関数から求めればよいです。
以上を踏まえて実装していきます。(ここまでで難しく感じる人もいるかもしれませんが、コードはかなりシンプルなのでコードを読むとわかるかもしれません)
実装
まず、考えられる全通りの盤面を用意します。seed0ではMが小さいため、その個数は意外と少なく、7623通りらしいです。BFSで実装しました。
// bfsで可能なすべての盤面を生成。Mが大きいときはTLE
vector<vector<vector<int>>> make_all_candidates() {
vector<vector<vector<int>>> q;
q.push_back(vector(N, vector(N, 0)));
rep(i, 0, M) {
vector<vector<vector<int>>> nq;
for(auto b : q) {
rep(j, 0, N - x_max[i]) rep(k, 0, N - y_max[i]) {
auto nb = b;
for(auto [x, y] : V[i]) {
nb[j + x][y + k]++;
}
nq.push_back(nb);
}
}
swap(nq, q);
}
return q;
}
これをもとに推定していきます。何もqueryを投げてない状態では、すべての状態の確率は等しいはずです。そして、①randomに点集合を選びクエリを投げる→②結果をもとに事前確率の配列を更新→③規格化→①...という感じでループしていき、最大の確率が一定を超えたら答えてみることを繰り返します。
// ベイズ推定をする
void bayesian_inference(vector<vector<vector<int>>> candidates) {
int n = candidates.size();
// 初期確率は全て等しい
vector<double> p(n, 1.0 / n);
while(1) {
// randomに点を20個選ぶ
int k = 20;
set<pair<int, int>> st;
while(st.size() < k) {
int i = rnd(N);
int j = rnd(N);
st.insert({i, j});
}
vector<pair<int, int>> v;
for(auto p : st) v.push_back(p);
// 点集合についてqueryを投げる
int res = query(v);
rep(i, 0, n) {
// i番目の盤面を仮定したときのv(S)の値を取得
int cnt = 0;
for(auto [x, y] : v) {
cnt += candidates[i][x][y];
}
// 事前確率に尤度を掛ける
p[i] *= lilelihood(k, cnt, res);
}
normalize(p);
auto max_it = max_element(p.begin(), p.end());
int max_ind = max_it - p.begin();
// 80%以上の確率で正解できそうなら聞いてみる
if(*max_it > 0.8) {
vector<pair<int, int>> v;
rep(i, 0, N) rep(j, 0, N) {
if(candidates[max_ind][i][j] > 0) v.push_back({i, j});
}
// 正解なら終了。だめならその事前確率を0にして継続
if(answer(v))
break;
else
p[max_ind] = 0.0;
}
}
}
この中で呼び出しているlikelihoodという関数が尤度を求めています。
点集合$S$を選んでクエリの結果が$res$であるとき、そのサイズを$k$、$B_j$から計算される$v(S)$を$cnt$とすると、求める尤度は、以下のように計算される平均、標準偏差をもつ正規分布の$res - 0.5$から$res + 0.5$までの部分の面積になります。(問題文から読み取りましょう。)
※指摘を受けて訂正しましたが、$res$が0の場合は$[-\infty,\ 0.5]$を見るのが正しいです。
// 個数k, v(S) = cntの点集合からresが得られたときの尤度(条件付き確率)
double lilelihood(int k, int cnt, int res) {
double mean = (k - cnt) * EPS + cnt * (1 - EPS);
double sigma = sqrt(k * EPS * (1 - EPS));
if(res == 0) return probability_in_range(-1e10, res + 0.5, mean, sigma);
return probability_in_range(res - 0.5, res + 0.5, mean, sigma);
}
以下が全体のコードになります。たったの?215行です
#include <bits/stdc++.h>
using namespace std;
#define rep(i, a, b) for(int i = a; i < (int)b; i++)
template <class T, class S>
bool chmax(T &a, const S &b) {
if(a < (T)b) {
a = (T)b;
return 1;
}
return 0;
}
template <class T, class S>
bool chmin(T &a, const S &b) {
if((T)b < a) {
a = (T)b;
return 1;
}
return 0;
}
// 乱数生成器
struct RandomNumberGenerator {
mt19937 mt;
RandomNumberGenerator()
: mt(chrono::steady_clock::now().time_since_epoch().count()) {}
int operator()(int a, int b) { // [a, b)
uniform_int_distribution<int> dist(a, b - 1);
return dist(mt);
}
int operator()(int b) { // [0, b)
return (*this)(0, b);
}
} rnd;
// 正規分布の累積分布関数
constexpr double normal_cdf(double x, double mean = 0.0, double sigma = 1.0) {
return 0.5 * (1.0 + std::erf((x - mean) / (sigma * 1.41421356237)));
}
constexpr double probability_in_range(double l, double r, double mean = 0.0,
double sigma = 1.0) {
assert(l <= r);
if(mean < l)
return probability_in_range(2.0 * mean - r, 2.0 * mean - l, mean,
sigma);
double p_l = normal_cdf(l, mean, sigma);
double p_r = normal_cdf(r, mean, sigma);
return p_r - p_l;
}
void normalize(vector<double> &v) {
double s = 0;
for(auto d : v) {
s += d;
}
assert(s > 0);
for(auto &d : v) {
d /= s;
}
}
// 質問query
int query(vector<pair<int, int>> v) {
cout << "q"
<< " " << v.size() << ' ';
for(auto [x, y] : v) {
cout << x << ' ' << y << ' ';
}
cout << endl;
int res;
cin >> res;
return res;
};
// 解答query
int answer(vector<pair<int, int>> v) {
cout << "a"
<< " " << v.size() << ' ';
for(auto [x, y] : v) {
cout << x << ' ' << y << ' ';
}
cout << endl;
int res;
cin >> res;
return res;
}
int N, M;
double EPS;
vector<vector<pair<int, int>>> V;
vector<int> x_max;
vector<int> y_max;
// 入力を受け取る。ついでに各ポリオミノの縦横の大きさも
void input() {
cin >> N >> M >> EPS;
V.resize(M);
x_max.resize(M);
y_max.resize(M);
rep(i, 0, M) {
int k;
cin >> k;
V[i].resize(k);
rep(j, 0, k) {
int x, y;
cin >> x >> y;
V[i][j] = {x, y};
chmax(x_max[i], x);
chmax(y_max[i], y);
}
}
}
// 個数k, v(S) = cntの点集合からresが得られたときの尤度(条件付き確率)
double lilelihood(int k, int cnt, int res) {
double mean = (k - cnt) * EPS + cnt * (1 - EPS);
double sigma = sqrt(k * EPS * (1 - EPS));
if(res == 0) return probability_in_range(-1e10, res + 0.5, mean, sigma);
return probability_in_range(res - 0.5, res + 0.5, mean, sigma);
}
// bfsで可能なすべての盤面を生成。Mが大きいときはTLE
vector<vector<vector<int>>> make_all_candidates() {
vector<vector<vector<int>>> q;
q.push_back(vector(N, vector(N, 0)));
rep(i, 0, M) {
vector<vector<vector<int>>> nq;
for(auto b : q) {
rep(j, 0, N - x_max[i]) rep(k, 0, N - y_max[i]) {
auto nb = b;
for(auto [x, y] : V[i]) {
nb[j + x][y + k]++;
}
nq.push_back(nb);
}
}
swap(nq, q);
}
return q;
}
// ベイズ推定をする
void bayesian_inference(vector<vector<vector<int>>> candidates) {
int n = candidates.size();
// 初期確率は全て等しい
vector<double> p(n, 1.0 / n);
while(1) {
// randomに点を20個選ぶ
int k = 20;
set<pair<int, int>> st;
while(st.size() < k) {
int i = rnd(N);
int j = rnd(N);
st.insert({i, j});
}
vector<pair<int, int>> v;
for(auto p : st) v.push_back(p);
// 点集合についてqueryを投げる
int res = query(v);
rep(i, 0, n) {
// i番目の盤面を仮定したときのv(S)の値を取得
int cnt = 0;
for(auto [x, y] : v) {
cnt += candidates[i][x][y];
}
// 事前確率に尤度を掛ける
p[i] *= lilelihood(k, cnt, res);
}
normalize(p);
auto max_it = max_element(p.begin(), p.end());
int max_ind = max_it - p.begin();
// 80%以上の確率で正解できそうなら聞いてみる
if(*max_it > 0.8) {
vector<pair<int, int>> v;
rep(i, 0, N) rep(j, 0, N) {
if(candidates[max_ind][i][j] > 0) v.push_back({i, j});
}
// 正解なら終了。だめならその事前確率を0にして継続
if(answer(v))
break;
else
p[max_ind] = 0.0;
}
}
}
int main() {
input();
bayesian_inference(make_all_candidates());
}
結果
seed0ではこんな感じになりました。
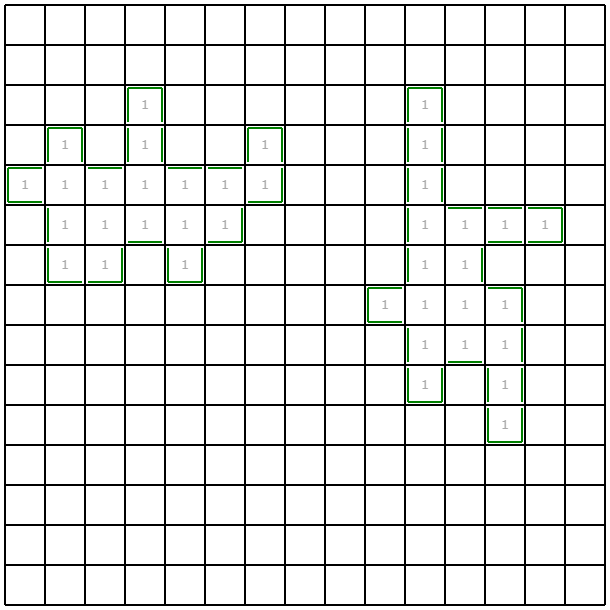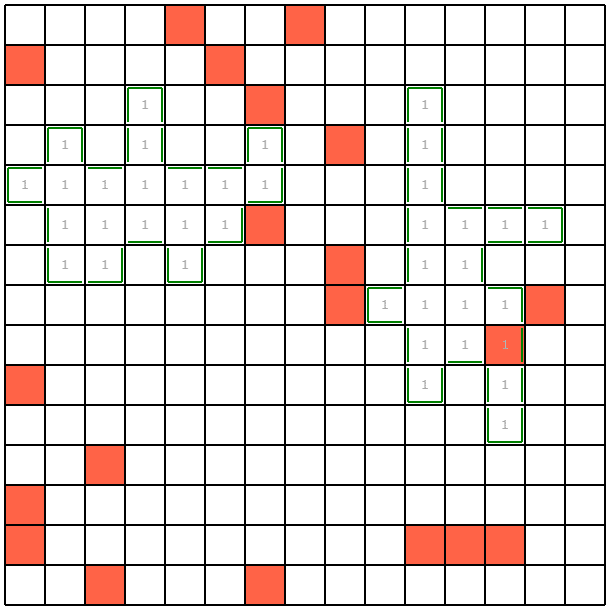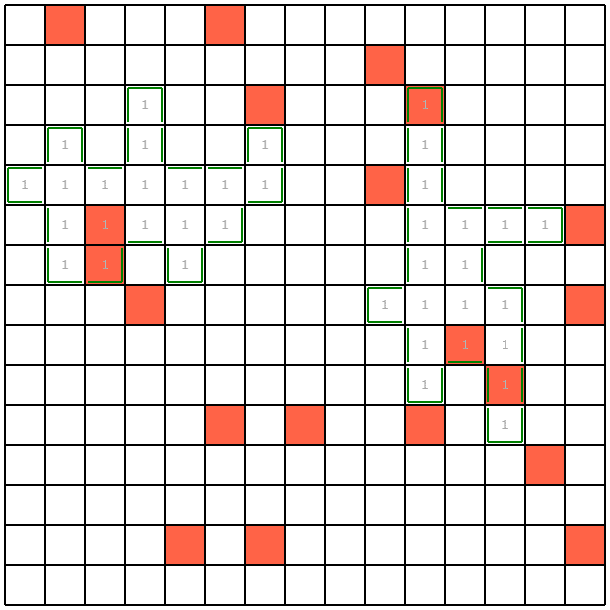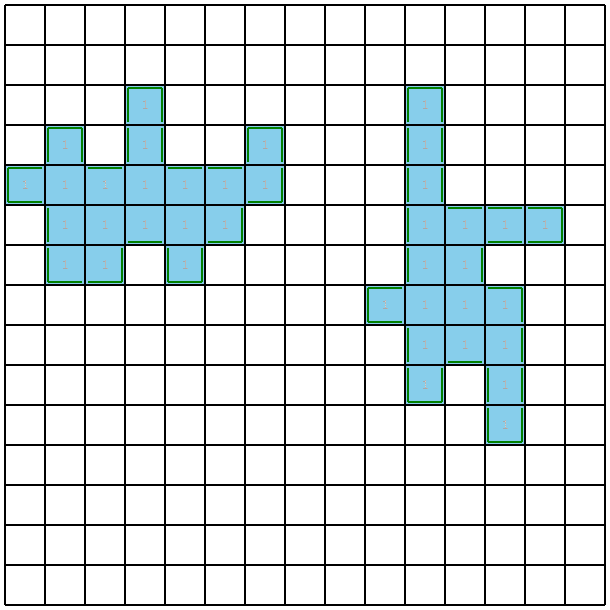
costは1.8くらいらしいです。
何がどうなって特定できているのかさっぱりわからない感じがかっこいいですね。
伸びしろなど
私の提出に比べてcostが大きいですが、点集合の選び方やbreak条件を適当にやっていることが伸びしろとして考えられます。ここからはぜひ自分で触って改良してみてください。
また、わかりやすさのために尤度をそのまま掛け算していますが、これは対数を取るほうがよかったり、規格化は実は不要だったりします。
最後に
一応できるだけわかりやすく書いたつもりですが、思ったよりも大変でした。
間違いがあれば教えてください。
今回は組み合わせが少ない場合にこれを書くだけで相当順位が上がる人も多いのではないでしょうか。