はじめに
業務中に音楽をシャッフル再生して開発効率をあげている皆様、こんばんは。
かくいう私もコーディングに集中するときはイヤホンつけていることが多いです。
しかしたまに、シャッフル再生にもかかわらず、「またGLAYかよ!」とか「同じ曲が二回続いた!」とか
「今日はJUDY AND MARYが多いな!」
ってことありませんか? きっとあるあるかとおもいます。
そして「これってほんとにランダムなの?」って音楽再生ソフトを疑うところまでが様式美です。
それ、多くの場合、自分の「ランダムってこうだよね」感にだまされています。
案外人間の感覚ってあてになりません。
それを体感するクイズをやってみましょう。
クイズ:どれがランダムでしょうか
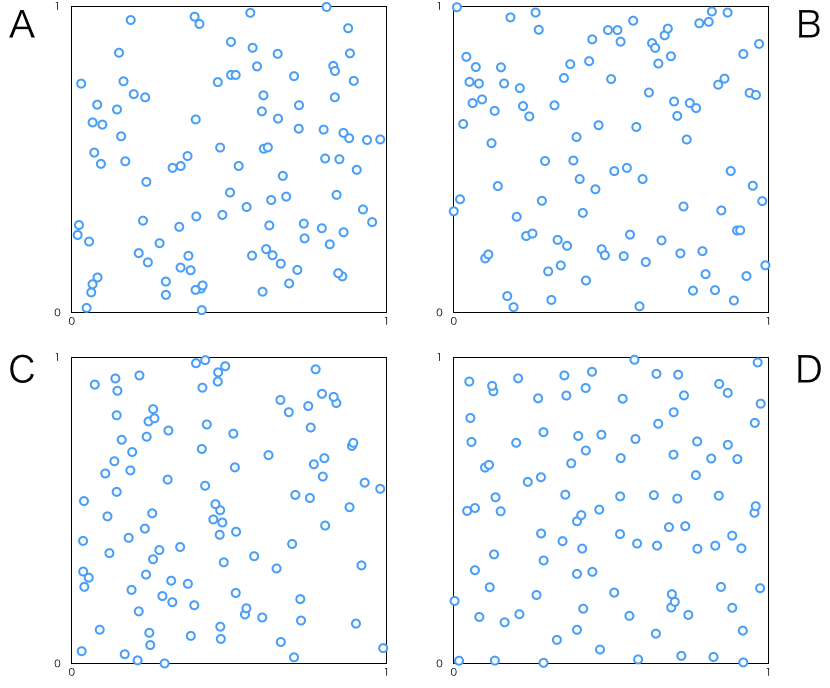
さて、A から D の[0 <= x,y <= 1]を満たす散布図を用意しました。
これら4つの図の中で完全にx,yの組がランダムに生成された図は1つだけです。あててみてください。
クイズ:答え合わせ
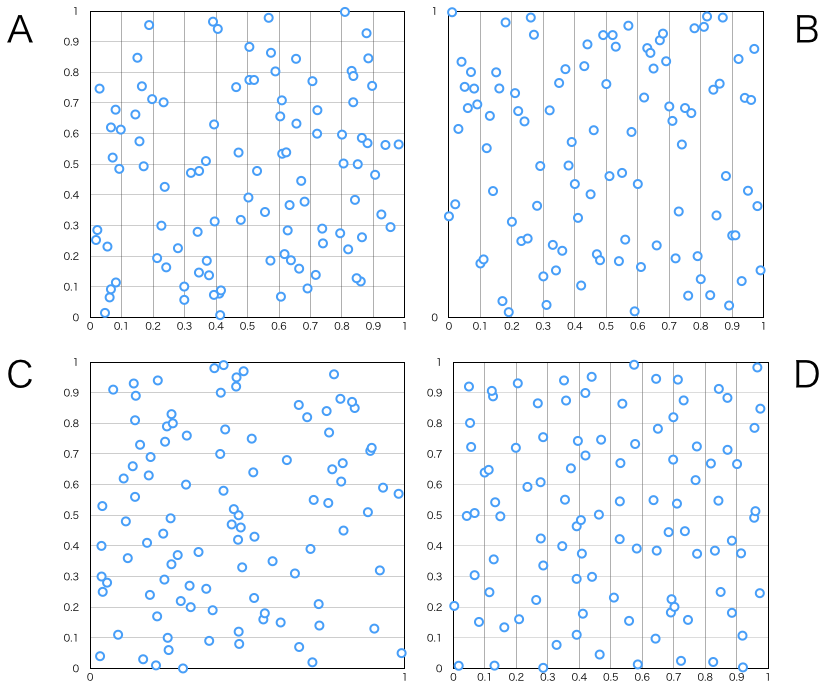
では種明かし。下記の図をみながらじっくりみていきましょう。
図D
図Dは下記のような数式を満たすプロットです。
x = 0.1 \times rand() + C_1 \\
y = 0.1 \times rand() + C_2
ここで rand() は 0 <= rand() < 1 を満たすランダム生成関数です。
この C の値を0から0.1刻みでプロットしています。
([C1, C2]が[0,0]から[0.9,0.9]までの100組をダブり漏れなく網羅するように刻んでいます。)
そのため、0.1 × 0.1 の箱の中に必ず1つの点が存在しています。
一番均等に散らばっているのでランダムに見えますが、図Dはランダムではありません。選んだ人残念。
図C
図Cは下記のような数式を満たすプロットです。
x = rand() \\
y = C
図Cでは、この C の値を0から0.01刻みでプロットしています。
つまり、y=[0, 0.01, 0.02,...] となっています。
わかりやすくするために、y軸に 0.1 刻みで目盛りを振っています。
横長長方形の中に、プロットが10個ずつ存在するのがわかると思います。
選んだ人残念。
図B
図Bは下記のような数式を満たすプロットです。
x = C \\
y = rand()
図Bでは、この C の値を0から0.01刻みでプロットしています。
ぶっちゃけ、図Cのx軸とy軸を入れ替えているだけのロジックです。
つまり、x=[0, 0.01, 0.02,...] となっています。
わかりやすくするために、x軸に 0.1 刻みで目盛りを振っています。
縦長長方形の中に、プロットが10個ずつ存在するのがわかると思います。
選んだ人残念。
図A
図Aは下記のような数式を満たすプロットです。
x = rand() \\
y = rand()
これが完全ランダムです。選んだ人すごい。
図Dと同じように0.1 × 0.1 の箱に区切ってみましたが、図Dと異なり、
プロットが存在しない箱、存在する箱、複数存在する箱といったランダム性があるのが一目瞭然かと思います。
音楽の例につなげると、GLAYが連続したり、JUDY AND MARY が1日に何回も流れてきたりすることこそが、
ランダムなのです。
おわりに
はじめにで紹介した、「またGLAYかよ!」とか「同じ曲が二回続いた!」とか
「今日はJUDY AND MARYが多いな!」という現象、ランダムだから起こるってことが伝わったでしょうか?
ランダムに懐疑的になる前に、自分の中のランダム感を疑いましょうという話でした。
(注意)
音楽再生ソフトのよっては シャッフル再生 = ランダム再生 ではないものも存在するかもしれません。
あくまでランダムを疑う例として音楽再生ソフトを話の導入に使ってみただけです。
(備考)
プログラム言語や表計算ソフトに実装されている rand() が厳密にいうとランダムではないという話はまた今度。
熱力学のシミュレーション屋だった自分からすると、かなーーーーり気にする話なのでそのうち書く。