の演習問題を解いているが解答が本書内にもネット上にもない模様。自分の解答を晒して間違いにツッコミをいただき理解を深めようという試み。
本章は正直消化できておらずわからない問題が多かったです。すみません。
- 問12.1
- いきなりすみません、わからず
- 問12.2
\begin{align}
Qの列が&正規直行だから\\
Q\hat{x}&=QQ^{\top}b\\
&=\mathbf{I}b\\
&=b\\
つまり\|Qx-b\|^2&=0\\
よって\|Qx-b\|&を最小化する。\\
行列とベクトルの&積だから計算量はO(N^2)\\
一般の最小二乗法は&O(N^3)なのでこの方法の方が計算量が少ない。
\end{align}
- 問12.3
- (a)
\begin{align}
A^{\dagger}&=(A^{\top}A)^{-1}A^{\top}\\
\\
(A_x)^{\top}(A\hat{x})&=(Ax)^{\top}(AA^{\dagger}b)\\
&=(Ax)^{\top}(A(A^{\top}A)^{-1}A^{\top}b)\\
&=(Ax)^{\top}(AA^{-1}(A^{\top})^{-1}A^{\top}b)\\
&=(Ax)^{\top}b\\
&=右辺
\end{align}
-
- (b)
\begin{align}
\frac{(Ax)^{\top}b}{\|A\hat{x}\|\|b\|}&=\frac{(Ax)^{\top}(A\hat{x})}{\|A\hat{x}\|\|b\|}\\
x&=\hat{x}とすると\\
&=\frac{\|A\hat{x}\|^2}{\|A\hat{x}\|\|b\|}\\
&=\frac{\|A\hat{x}\|}{\|b\|}
\end{align}
-
- (c) わからず
-
問12.4
- (a)
\begin{align}
&\sum_{i=1}^m{w_i(\tilde{a}_i^{\top}x-b_i)^2}\\
D&=\begin{bmatrix}
w_1 & & & \\
& w_2 & 0 & \\
& 0 & \ddots & \\
& & & w_m \\
\end{bmatrix}\\
&とおけば\\
与式&=\|D(Ax-b)\|^2と表せる。
\end{align}
-
- (b) B=DAはAの各要素を定数化するだけだからBの列も線型独立
-
- (c) わからず
-
問12.5
\begin{align}
X&=A^{\dagger}とすると\\
R&=AX-I\\
&=AA^{\dagger}-I\\
&=A(A^{\top}A)^{-1}A^{\top}-I\\
&=AA^{\top}(A^{\top})^{-1}A^{\top}-I\\
&=II-I\\
&=0\\
\therefore X&=A^{\dagger}
\end{align}
-
問12.6 わからず
-
問12.7
\begin{align}
d&=(d_1, d_2, \cdots, d_n)^{\top}\\
P&=\begin{bmatrix}
P_{11} & P_{12} & \cdots & P_{1n} \\
P_{21} & & & \\
\vdots & & \ddots & \vdots \\
P_{N1} & & & P_{Nn} \\
\end{bmatrix}\\
t&=(t_1, t_2, \cdots, t_N)^{\top} \\
とおくと\\
Pd-t&の最小化となるので、\\
\|Pd-t\|^2&の最小二乗問題として解けばよい(でよいか?)
\end{align}
- 問12.8 これで良いかな?
\begin{align}
(A^{\top}A)^{-1}A^{\top}b&=A^{-1}(A^{\top})^{-1}A^{\top}b \\
&=A^{-1}b
\end{align}
-
問12.9 わからず
-
問12.10
import numpy as np
np.random.seed(12345)
A = np.matrix(np.random.rand(30, 10))
b = np.matrix(np.random.rand(30, 1))
A_inv = np.linalg.pinv(A)
x_hat = A_inv @ b
x_hat
matrix([[ 0.02934915],
[-0.01803483],
[-0.21125115],
[ 0.22084766],
[ 0.25645909],
[ 0.42175874],
[-0.05059225],
[-0.26162219],
[ 0.1031212 ],
[ 0.56314294]])
print(np.linalg.norm(A @ x_hat - b, ord=2) ** 2)
d1 = np.matrix(np.random.rand(10, 1))
d2 = np.matrix(np.random.rand(10, 1))
d3 = np.matrix(np.random.rand(10, 1))
print(np.linalg.norm(A @ (x_hat - d1) - b, ord=2) ** 2)
print(np.linalg.norm(A @ (x_hat - d2) - b, ord=2) ** 2)
print(np.linalg.norm(A @ (x_hat - d3) - b, ord=2) ** 2)
1.146449535889748
214.71361908208476
37.71643878027834
186.70727959830037
よって、\|A(\hat{x}-d)-b\|^2\gt\|A\hat{x}-b\|^2 が成り立つ
-
問12.11 わからず
-
問12.12 わからず
-
問12.13
- (a)
\begin{align}
x^{(k+1)}&=x^{(k)} より\\
x^{(k+1)}&=x^{(k)}-\mu A^{\top}(Ax^{(k)}-b) \\
\therefore \mu A^{\top}(Ax^{(k)}-b)&=0 \\
A(x^{(k)}-b)&=0\\
つまりx^{(k)}&=\hat{x}
\end{align}
-
- (b)
x^{(k)}-\mu A^{\top}(Ax^{(k)}-b)=(1-\mu A^{\top}A)x^{(k)}+\mu A^{\top}b
-
- (c) プログラム
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(123456)
A = np.matrix(np.random.rand(20, 10))
b = np.matrix(np.random.rand(20, 1))
A_inv = np.linalg.pinv(A)
x_hat = A_inv @ b
print(x_hat)
mu = 1 / np.linalg.norm(A, ord=2) ** 2
print(mu)
[[ 0.37578839]
[ 0.06913825]
[ 0.01868794]
[ 0.31121314]
[-0.05678396]
[ 0.11069005]
[-0.48839542]
[ 0.35651823]
[-0.16093131]
[ 0.38029278]]
0.018815612455252692
x = np.matrix([[0]] * 10)
x_out = x.T.tolist()
for k in range(500):
x = x - mu * A.T @ (A @ x - b)
x_out.append(x.T.tolist())
plt.figure(figsize=(8, 8))
for i in range(10):
li_plot = []
for k in range(1, 500):
li_plot.append(x_out[k][0][i])
plt.plot(list(range(1, 500)), li_plot, label=i)
plt.axhline(y=x_hat[i], linestyle='dashed', color='darkgray')
plt.legend()
plt.show()
-
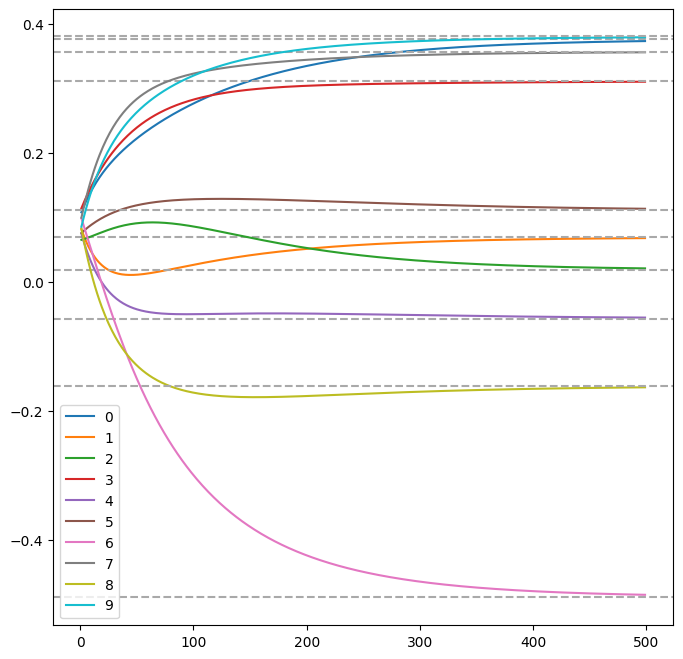
- 10要素をまとめて表示したが、それぞれ$$\hat{x}$$の各要素(灰色破線)に収束している
-
問12.14
- (a)
\begin{align}
(12.8)より\\
\hat{x}&=(A^{\top}A)^{-1}A^{\top}b \\
\hat{x}^{(k)}&=\{(A^{(k)})^{\top}A^{(k)}\}^{-1}(A^{(k)})^{\top}b^{(k)}\\
&=(G^{(k)})^{-1}h^{(k)}
\end{align}
-
- (b)
\begin{align}
G^{(k+1)}&=(A^{(k+1)})^{\top}A^{(k+1)} \\
&=\sum_{i=1}^{k+1}{a_ia_i^{\top}} \\
&=\sum_{i=1}^{k}{a_ia_i^{\top}} + a_{k+1}a_{k+1}^{\top} \\
&=G^{(k)}+a_{k+1}a_{k+1}^{\top}\\
\\
h^{(k+1)}&=\sum_{i=1}^{k+1}{b_ia_i} \\
&=\sum_{i=1}^{k}{b_ia_i} + b_{k+1}a_{k+1} \\
&=h^{(k)}+b_{k+1}a_{k+1}
\end{align}
-
- (c)
\begin{align}
&G^{(k+1)}にはG^{(k)}とa_{k+1}a_{k+1}^{\top}の計算が必要\\
&G^{(k)}の計算量は無視すると\\
&a_{k+1}a_{k+1}^{\top}はn次元ベクトルの内積だから計算量はn\\
&同様にh^{(k+1)}の計算量もb_{k+1}a_{k+1}を考えるとn\\
&(a)の計算量はmn\\
&これがm回繰り返されるから\\
&n(2n+mn)=2n^2+mn^2
\end{align}
- 問12.15
\begin{align}
\|(Ax-b)+f\|^2&=\|Ax-b\|^2+2f\|Ax-b\|+f^2\\
2A^{\top}fx&=c^{\top}xならば与式が満たされるから\\
2A^{\top}f&=c^{\top}\\
f&=\frac{1}{2}(A^{\dagger})^{\top}c\\
よってf&=\frac{1}{2}(A^{\dagger})^{\top}cとおけば与式が成り立つ
\end{align}
- 問12.16 わからず