数学は楽をするためにある
厳密な議論はしません。こんなものだとイメージをもってから正式なテキストで学んだほうがよいと思うので。
ただ詳しい方、間違っていたら教えてくださいな。
機械学習のために必要な数学
機械学習のために必要な数学ってなんだろう。
純粋な数学科の数学の場合は、例えば「岩波現代数学への入門」の『現代数学の流れ1』に学ぶべき流れが書かれている。左記に書かれているものとは若干異なるが、このシリーズを読まれた方がまとめた参考記事。
「現代数学への入門」
工学系で学ぶべき数学の場合は、例えば
東京大学工学教程 基礎系数学
で機械学習は動向が早いためかカチッとしたものが見当たらないですが、例えば
六本木で働くデータサイエンティストのブログ:機械学習をやる上で必要な数学とは、どの分野のどのレベルの話なのか(数学が大の苦手な人間バージョン)
また、私がまとめたもの
データサイエンス、データ分析、機械学習に必要な数学
データサイエンス、データ分析、機械学習に必要な数学2
があります。
で今回は、数学記号、公理・定義・定理、微分積分に慣れるところ。
数学記号
まず記号が嫌いという方もいるだろう。
a \\
b \\
c \\
i \\
j \\
k \\
x \\
y \\
z \\
なんていっぱい出てくるし
x^i \\
x_i \\
x_i^k
?右上に小さな数字がつくのは累乗だけど右下は数列?上下になんかついているぞ。
\sin \\
\cos \\
\tan \\
\sum \\
\prod \\
\lim \\
\frac{dx}{dy} \\
\int \\
Out!
と投げ出さないで。一つづつ説明を聞くと愛着も出て来ようもの。
なんでこんなややこしいことを読み書きしなければならないのか。これには大きく分けて2つの意味がある。
定義を厳密にし、数学理論を精緻化するため
うん、これは自分には関係ないけどわかる。でも関係ない。だいたい分かればいいのに。そうだねこれは研究者がやればいい。いや我々に大切なのはもう一つの方
楽をするため!
!!!
x, y, z 変数
変数とは値を代入する箱のようなもの。x, y, zを使われることが多く、足りない場合はwや他の記号を使う場合もある。もっと足りない場合は後述の添字を用いる。
y=x^2+1 のグラフ
などのように、xに何らかの値を入れるとyが求まり、xを変えるとyも変わる。このように変数を用いる。
a, b, c 定数
a, b, cを使われることが多く、足りない場合はd, e, f,... と他の記号を使う場合もある。定数とは変数に似ているけど少し違う。値を入れる箱なのだがその議論の中では変化しない数を入れる。
y=ax+b のグラフ
のようにaとbに何らかの数字が入り、xを変えていくとyが変わるね、のような場合、この議論の中ではaとbの値は変化しない。
y=2x-1 \\
y=-3x+6 \\
...
のように無数に考えられるけどそれらをすべて書いてられないので、こういった式の(一次式と呼ばれる)性質を調べる時に
a, bは何らかの値が入る定数、x, yは一方を変えると一方が式に則り値が変わる変数、ということを示すために変数、定数、を用いる。
i, j, k 変数
これも変数だが自然数を示すことが多くまた、下の添字として使われることが多い。
添字
x_i
などとして使われる。変数がx, y, zでは足りなくてn個あるような場合はこのように添え字を使って表現する。
∑ 足し算しているだけ
1から100までを足す場合は、100個も数字を書いてられないし
1+2+3+……+100=5050
なんて書いたりする。
単なる整数の足し算ならいいがもっと複雑な式の場合はいちいち書いてられない。で
\sum_{k=1}^{100}{k}=1+2+3+……+100=5050
なだけ。変数になるとちょっとビックリするけど
\sum_{k=1}^{n}{x_k}=x_1+x_2+x_3+......+x_n
なだけ。なれないうちは上のように具体的に足し算にしてみたらいい。
Π 掛け算しているだけ
∑の掛け算版。
機械学習だと確率の掛け算が多数出てきてΠが登場してくる。
\prod_{i=1}^{5}=1\times2\times3\times4\times5=120
なだけ。これも変数になるとちょっとビックリするけど
\prod_{k=1}^{n}{x_k}=x_1\times x_2\times x_3\times ...... \times x_n
なだけ。
公理、定義、定理
c.f. https://www.beret.co.jp/books/tachiyomi/images/629.pdf
なんか似たような言葉でぐんぐん押してくるよね数学書って。
- 公理
- このあとの話を進めるにあたっての前提、仮定みたいな。公理のまとまり上で議論するので公理系と言ったりする。世界観って感じ。平面上っていう公理系(世界観)では三角形の内角の和は180°になるけど曲面上という公理系(世界観)ならば180°にならなかったり。でも当たり前な場合はわざわざ「公理」として示さない場合もある。
- 定義
- 決めごと。こう決めますということ。「点とは部分を持たないものである」が有名。「~~とは」っていう文章になる。
- 定理
- 公理の世界観の中で、定義とすでに証明された定理のみから論理的に分かる、定められること。証明が必要。
- 何もかも全くわからない
- 前書き等にある前提知識に立ち戻る必要あり
- 分かった気にはなるが、定理→証明と読み進めていくとだんだん分からなくなる
- 繰り返し読むか
- 正確性は落としても説明の優しい本で準備運動
- 証明ではなく、定理のあとにやわらかな説明をしてある。前書きで「数学的厳密性は追わない」というような本。本文で定理はあっても「証明は略す」とあり、説明書きや図解があるような本
- あるいは例題が豊富な問題集で具体的な問題を解いて定理を自分になじませる
が必要。
微分積分
微分:難しいものは細かく分けて、分けたものの性質を調べるほうが簡単だね
積分:細かく分けあたあとその性質を足し合わせればもとの難しいものの性質がわかるね
ってな感じ。
機械学習では実データに対して、それに合っているようなモデルとなる式を考える。当然誤差があるので、その誤差が小さくなるように頑張る。実データは通常複雑なので直線でOKなんてことはなく、モデルとなる式はかなり複雑となる。でも我々が知りたいのは通常は誤差が小さくなることなので、
極限
ある変数xが別の値aに「限りなく近づく」とき
\lim_{x \to a}
を用いて表す。数学的により正確には「限りなく近づく」という表現ではなくイプシロンデルタ論法を用いる。
例
1/xのxが限りなく0に近づくとき
\lim_{x \to 0}{\frac{1}{x}}=\infty
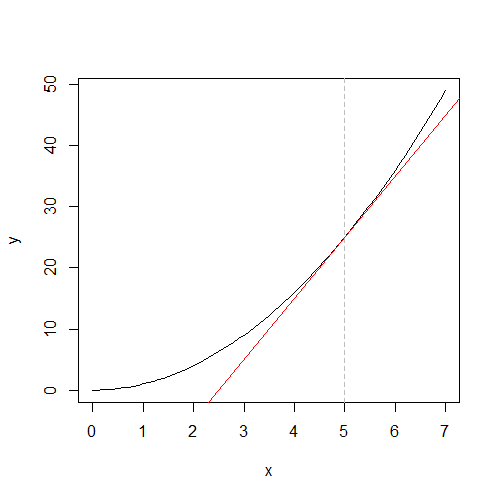
微分
f(x)のx~x+\Delta xでの傾き = \frac{f(x+\Delta x)-f(x)}{\Delta x} \\
だが\Delta xをどんどん小さくしていくと、f(x)のxでの傾きがわかり
f'(x)=\lim_{\Delta x\rightarrow 0}\frac{f(x+\Delta x)-f(x)}{\Delta x}
をf(x)の導関数という。
また、導関数を求めることを、微分する、という。
これだけ。
\begin{align}
f(x)&=x^2 の場合 \\
f'(x)&=(x^2)' \\
(x^2)'&=\lim_{\Delta x\rightarrow 0}\frac{(x + \Delta x)^2-x^2}{\Delta x} \\
&=\lim_{\Delta x\rightarrow 0}\frac{x^2 + 2\Delta x x+(\Delta x)^2 - x^2}{\Delta x} \\
&=\lim_{\Delta x\rightarrow 0}(2x+\Delta x) \\
&=2x
\end{align}
までは簡単だね。でも数学はいつでも成り立つように一般化する。
\begin{align}
f(x)&=x^n (nは正の整数)の場合 \\
(x^n)'&=\lim_{\Delta x\rightarrow 0}\frac{(x + \Delta x)^n-x^n}{\Delta x} \\
(x + \Delta x)^n なんてどうするの?
\end{align}
微分が難しいというのは実は微分自体が難しいのではなくて、過去それまでに学んだ蓄積をほぼ全て使うから、それらを忘れていると次に進めない難しさだったりする。
-
二項定理!
- c.f. Wikipedia:二項定理
- c.f. 統計学のための数学入門30講のp.17 2項定理と多項定理
(a+b)^n = \sum_{k=0}^n{_nC_ka^kb^{n-k}} \\
_nC_k = \frac{n!}{(n-k)!k!}
のでので、
\begin{align}
(x + \Delta x)^n &= \sum_{k=0}^n{_nC_kx^k\Delta x^{n-k}} \\
&= \sum_{k=0}^n{\frac{n!}{(n-k)!k!}x^k\Delta x^{n-k}}
\end{align}
のでのでので、
\begin{align}
(x^n)'&=\lim_{\Delta x\rightarrow 0}\frac{(x + \Delta x)^n-x^n}{\Delta x} \\
&=\lim_{\Delta x\rightarrow 0}\frac{\sum_{k=0}^n{\frac{n!}{(n-k)!k!}x^k\Delta x^{n-k}}-x^n}{\Delta x} \\
k=n-1までとk=nを場合分けして \\
&=\lim_{\Delta x\rightarrow 0}\frac{\sum_{k=0}^{n-1}{\frac{n!}{(n-k)!k!}x^k\Delta x^{n-k}}+\frac{n!}{(n-n)!n!}x^n\Delta x^{n-n}-x^n}{\Delta x} \\
分子の第2項は消えて\\
&=\lim_{\Delta x\rightarrow 0}\frac{\sum_{k=0}^{n-1}{\frac{n!}{(n-k)!k!}x^k\Delta x^{n-k}}}{\Delta x} \\
&=\lim_{\Delta x\rightarrow 0}\sum_{k=0}^{n-1}{\frac{n!}{(n-k)!k!}x^k\Delta x^{n-k-1}} \\
k=n-1以外は\Deltaが残り0になり、k=n-1とすると \\
&=\frac{n!}{(n-(n-1))!(n-1)!}x^{n-1} \\
&=nx^{n-1}
\end{align}
という長たらしい式になって面倒ではあるけど、難しいというよりも定義に乗っかるだけ。これが三角関数でも他の複雑な関数でも同じ。傾きを出しているだけ。
積分
関数y=f(x)で囲まれた範囲の面積を考える
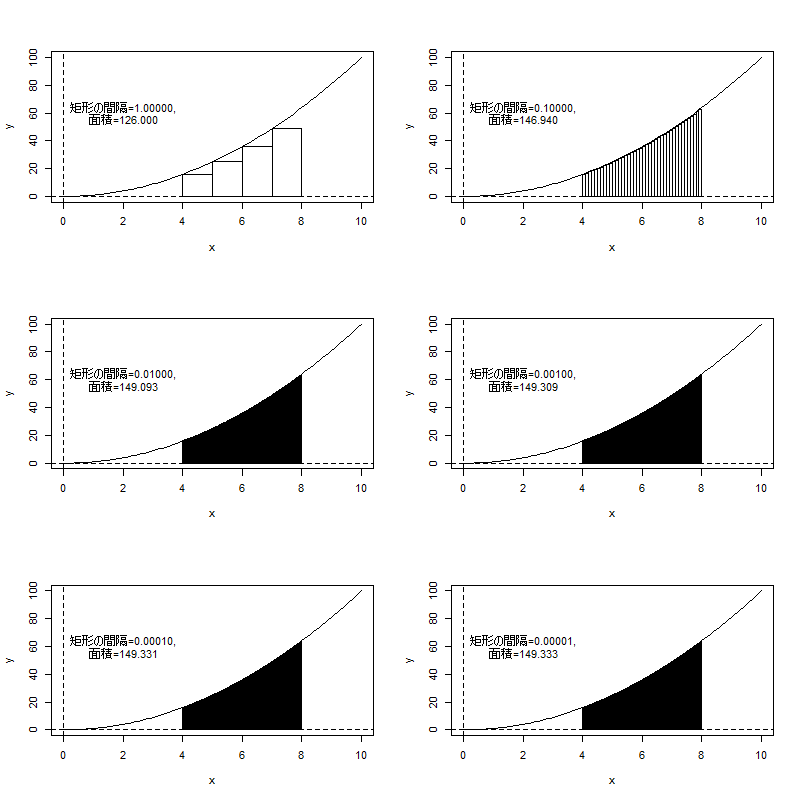
y=x^2の関数と4<=x<=8, y=0で囲まれた面積を考える
まず、図の左上、xを1ずつずらした矩形の面積を足すことを考える。これだと面積は126となるが、矩形とx^2の間に隙間が多すぎる。
もっとxの間隔を細かくして0.1ずつとすると図の右上、面積は146.94となる。かなり隙間は埋まったがまだ隙間が残る。
というわけでxをずらす間隔を1/10ずつどんどん細かくしていくと面積は149.333程度で落ち着きそう。ただ、この図では真っ黒に埋まって
しまったが、実際には曲線のx^2に対して矩形を当てはめているので隙間が残っている。
この隙間は範囲aからbをn分割するように
\Delta{x}=\frac{b-a}{n}
と置く(上の例ではa=4, b=8)。また
x_k=a+k\Delta{x}
なので矩形の高さは
f(x_k)
となり、矩形の面積は
f(x_k)\Delta{x}
となる。求める面積は上記をすべて足し合わせるので、
\sum_{k=0}^{n-1}{f(x_k)\Delta{x}}
となり、間隔を無限小まで小さくすればいいので、面積は結局
\lim_{n \to \infty}{\sum_{k=0}^{n-1}{f(x_k)\Delta{x}}} \\
\Delta{x}=\frac{b-a}{n}
となる。記号がややこしいのであらためて
\lim_{n \to \infty}{\sum_{k=0}^{n-1}{f(x_k)\Delta{x}}}=\int_a^b{f(x)dx}
としたものが積分記号のインテグラルです。
微積分学の基本定理
c.f. Wikipedia:微積分学の基本定理
\begin{align}
F(x)&=\int_a^x{f(t)dt} \\
\frac{d}{dx}F(x)&=\frac{d}{dx}\int_a^x{f(t)dt}=f(x)
\end{align}
あるいは
\begin{align}
\int_a^b{f(x)dx}&=\left[F(x)\right]_a^b \\
&=F(b)-F(a)
\end{align}
つまり微分してf(x)となる関数F(x)を求めるのが積分というわけです。
例
\begin{align}
\frac{d}{dx}x^2&=2x \\
\frac{1}{2}\frac{d}{dx}x^2&=x
\end{align}
ならば、
\int{xdx}=\frac{1}{2}x^2+C
最後のCは積分定数と言って、Cにどんな定数があっても右辺を微分するとxになるので、決まらないけど定数がありますよとの意味でCとつけておく(不定積分)。積分の範囲が決まっていればその値を代入すればCが求まる(定積分)
先程の面積の正確な値は
\begin{align}
\int_4^8{x^2dx}&=\left[\frac{1}{3}x^3\right]_4^8 \\
&=\frac{1}{3}(512-64) \\
&=\frac{448}{3} \\
&=149.\dot{3}
\end{align}