LoginSignup
1
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?

@aokikenichi(青木 健一)

その株価予測間違っています！初心者注意！LSTMによる時系列予測のよくある間違い

Last updated at Posted at 2025-07-20

LSTMによる株価予測に気をつけろ

Qiita記事のLSTMによる株価予測は間違いが多いです
正確に言うと間違いというより、正しい学習モデルではないです

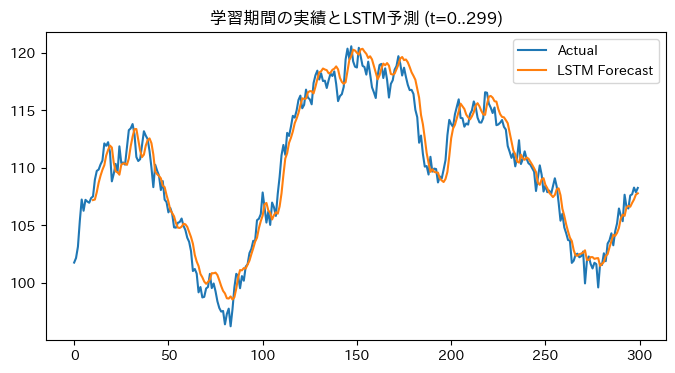
過去の株価からLSTMで学習し予測しました。かなり正確に予測できていると思います！

とこんなグラフを示している記事をよく見ます。
今回は株価ではなく、架空の株価を模したランダムウォークです。

image.png

青の実績値についてオレンジのLSTMの予測値がかなりよく予測できているように「見えます」
誤差指標で見ても、学習期間 (t=10..299)で、

RMSE MAPE
LSTM 1.2806 0.94%

誤差率1%未満です。

これ合っているのでしょうか？

ある意味あっていると言えば合っていますよね。ただ細かく見ていくと例えば160-180時点の当たりなど実績値の下落を後追いで示しているだけですね。これって使える予測でしょうか？

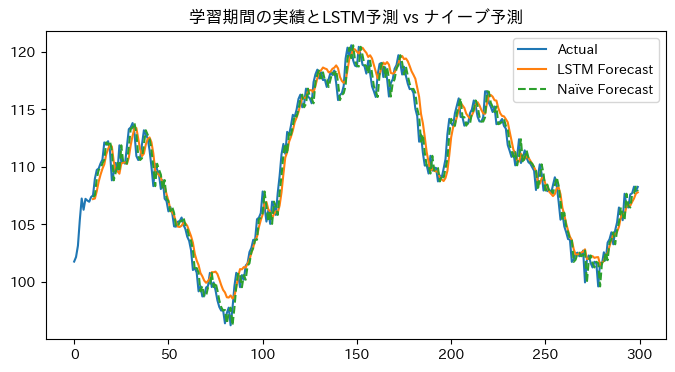
ここに別の 「予測」 を重ねます。ナイーブ予測というものです。

image.png

指標で見てもナイーブ予測の方が精度が良いです。

RMSE MAPE
LSTM 1.2806 0.94%
Naïve 0.9928 0.74%

オレンジのLSTMよりもナイーブ予測の点線の方が良くない？これどういうDeep Learning?
これは単に今の実績値の1時点先にずらしたものを「予測」値とするという方法です。1時点スライドするだけ。

もし株価予測で今日の値を明日の予測値とするで利益が上がるのならLSTMなんかする必要なくナイーブ予測で十分で、LSTMはむしろ精度が悪いです。
そして、ナイーブ予測は、今日の値を明日の予測とするは上がり基調、下がり基調の時はある程度有用ですが上下反転した時や上下動を繰り返すときに痛い目をみます。→事実上株価予測には使えないですよね。

そして何が辛いって単に過去の実績値を説明変数としたLSTMはナイーブ予測よりも劣化版ということです（絶対ナイーブ予測より悪いということではなく、少なくとも大きく改善することはないということです）。

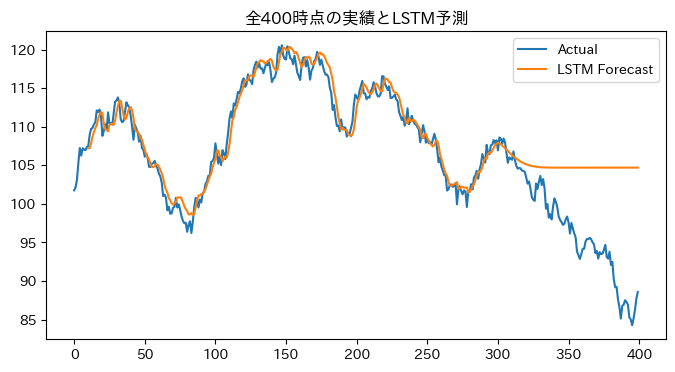
ちなみにこのモデルで未来を予測しようとすると、ほぼ何も学習できておらず過去の値の平均値的な値を予測して終わりです。ナイーブモデルなら未来でも今の値が次の値になりますけど。

image.png

まとめ

  • 本記事は初心者の方をdisることは目的としていません
    • LSTMによる株価予測を実施しました、で上記の罠にハマっている記事はQiitaだけでなく世の中にたくさん溢れています。そしていいねがたくさんついており、注目されているのかなと思います。
    • 「LSTMを学び株価を予測したらこうなりました」の記事だったらそれは良いと思います。ただ、上記状況なのに「かなり良い学習ができています」という理解の場合、後で絶対苦労しますので。ここを要注意ということです。
  • また、LSTMによる時系列予測をdisるための記事でもないです
    • 時系列に特徴的なパターンがあったり、他の説明変数を追加などできればLSTMは強力なアルゴリズムです

コード例

ChatGPT o4-mini-highで作りました。

架空の株価風データをランダムウォークで生成し、それをLSTNで予測するプログラムを書いて
仕様
400時点生成
PyTorchでLSTNを用い300時点で学習
300時点+100時点全400時点の予測
300時点の実績値と予測値をプロット
300時点の実績値と全400時点の予測をプロット
300時点の実績値と予測値と実績値を1つ横にスライドしたナイーブ予測をプロット
実績値と予測値、実績値とナイーブ予測のRMSE、MAPEを出力

  • LSTMの予想が間違って一直線だったり予測値の表示がずれていたりの訂正を10回以上繰り返して、下記コードに
!pip install japanize-matplotlib
import japanize_matplotlib

import numpy as np
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import TensorDataset, DataLoader
from sklearn.preprocessing import StandardScaler
import matplotlib.pyplot as plt

# ──────────────────────────────────────
# 1) ハイパーパラメータ＆シード
# ──────────────────────────────────────
SEED        = 0
TIME_POINTS = 400
TRAIN_CUT   = 300
SEQ_LEN     = 10
BATCH_SIZE  = 32
N_EPOCHS    = 5   # デモ用に少なめ。必要に応じて増やしてください
HIDDEN_SIZE = 32
LR          = 1e-2

np.random.seed(SEED)
torch.manual_seed(SEED)

# ──────────────────────────────────────
# 2) ランダムウォークで架空株価を生成 + 標準化
# ──────────────────────────────────────
raw_prices = 100 + np.cumsum(np.random.randn(TIME_POINTS))
scaler     = StandardScaler()
prices     = scaler.fit_transform(raw_prices.reshape(-1,1)).flatten()

# ──────────────────────────────────────
# 3) シーケンス化
# ──────────────────────────────────────
def make_seq(data, L):
    X, Y = [], []
    for i in range(len(data) - L):
        X.append(data[i:i+L])
        Y.append(data[i+L])
    return np.array(X), np.array(Y)

X_np, Y_np = make_seq(prices[:TRAIN_CUT], SEQ_LEN)

# ──────────────────────────────────────
# 4) DataLoader
# ──────────────────────────────────────
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
X_train = torch.from_numpy(X_np).float().unsqueeze(-1).to(device)
Y_train = torch.from_numpy(Y_np).float().to(device)
loader  = DataLoader(TensorDataset(X_train, Y_train), batch_size=BATCH_SIZE, shuffle=True)

# ──────────────────────────────────────
# 5) LSTMモデルトレーニング
# ──────────────────────────────────────
class LSTM(nn.Module):
    def __init__(self):
        super().__init__()
        self.lstm = nn.LSTM(1, HIDDEN_SIZE, batch_first=True)
        self.fc   = nn.Linear(HIDDEN_SIZE, 1)
    def forward(self, x):
        out, _ = self.lstm(x)
        return self.fc(out[:, -1, :]).squeeze()

model = LSTM().to(device)
opt   = optim.Adam(model.parameters(), lr=LR)
crit  = nn.MSELoss()

for _ in range(N_EPOCHS):
    model.train()
    for xb, yb in loader:
        opt.zero_grad()
        loss = crit(model(xb), yb)
        loss.backward()
        opt.step()

# ──────────────────────────────────────
# 6) 予測
# ──────────────────────────────────────
model.eval()
with torch.no_grad():
    train_s = model(X_train).cpu().numpy()
train_pred = scaler.inverse_transform(train_s.reshape(-1,1)).flatten()

future_s = []
last_seq = torch.from_numpy(prices[TRAIN_CUT-SEQ_LEN:TRAIN_CUT])\
                 .float().unsqueeze(0).unsqueeze(-1).to(device)
for _ in range(TIME_POINTS - TRAIN_CUT):
    with torch.no_grad():
        p = model(last_seq).item()
    future_s.append(p)
    last_seq = torch.cat([last_seq[:,1:,:], torch.tensor([[[p]]], device=device)], dim=1)

full_s   = np.concatenate([train_s, np.array(future_s)])
full_pred= scaler.inverse_transform(full_s.reshape(-1,1)).flatten()

naive_s  = X_np[:, -1]
naive_pred = scaler.inverse_transform(naive_s.reshape(-1,1)).flatten()

# ──────────────────────────────────────
# 7) グラフ1: 全400点の実績とLSTM予測
# ──────────────────────────────────────
forecast = np.full(TIME_POINTS, np.nan)
forecast[SEQ_LEN:] = full_pred

plt.figure(figsize=(8,4))
plt.plot(raw_prices, label="Actual")
plt.plot(forecast,    label="LSTM Forecast")
plt.title("全400時点の実績とLSTM予測")
plt.legend()
plt.show()

# ──────────────────────────────────────
# 8) グラフ2: 学習区間の実績とLSTM予測 (t=0..299)
# ──────────────────────────────────────
plt.figure(figsize=(8,4))
plt.plot(raw_prices[:TRAIN_CUT], label="Actual")
plt.plot(np.arange(SEQ_LEN, TRAIN_CUT), full_pred[:TRAIN_CUT-SEQ_LEN], label="LSTM Forecast")
plt.title("学習期間の実績とLSTM予測 (t=0..299)")
plt.legend()
plt.show()

# ──────────────────────────────────────
# 9) グラフ3: 学習区間にナイーブ予測を追加
# ──────────────────────────────────────
naive_pad = np.full(TRAIN_CUT, np.nan)
naive_pad[SEQ_LEN:] = naive_pred
plt.figure(figsize=(8,4))
plt.plot(raw_prices[:TRAIN_CUT], label="Actual")
plt.plot(np.arange(SEQ_LEN, TRAIN_CUT), full_pred[:TRAIN_CUT-SEQ_LEN], label="LSTM Forecast")
plt.plot(naive_pad, linestyle="--", label="Naïve Forecast")
plt.title("学習期間の実績とLSTM予測 vs ナイーブ予測")
plt.legend()
plt.show()


from sklearn.metrics import mean_squared_error, mean_absolute_percentage_error

# ──────────────────────────────────────
# 評価指標の計算：学習期間 t=10..299
# ──────────────────────────────────────
# 実績
actual_train = raw_prices[SEQ_LEN:TRAIN_CUT]                     # length = 290
# LSTM予測（full_pred は逆標準化済み）
lstm_train   = full_pred[:TRAIN_CUT-SEQ_LEN]                    # length = 290
# ナイーブ予測
naive_train  = naive_pred                                       # length = 290

# RMSE, MAPE の計算
rmse_lstm  = np.sqrt(mean_squared_error(actual_train, lstm_train))
mape_lstm  = mean_absolute_percentage_error(actual_train, lstm_train) * 100

rmse_naive = np.sqrt(mean_squared_error(actual_train, naive_train))
mape_naive = mean_absolute_percentage_error(actual_train, naive_train) * 100

# 結果を表示
print("=== 学習期間 (t=10..299) の評価指標 ===")
print(f"LSTM    → RMSE: {rmse_lstm:.4f}, MAPE: {mape_lstm:.2f}%")
print(f"Naïve   → RMSE: {rmse_naive:.4f}, MAPE: {mape_naive:.2f}%")

時系列予測・需要予測について本格的に学びたくなったら

1
0
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
1
0

Delete article

Deleted articles cannot be recovered.

Draft of this article would be also deleted.

Are you sure you want to delete this article?