の演習問題を解いているが解答が本書内にもネット上にもない模様。自分の解答を晒して間違いにツッコミをいただき理解を深めようという試み。
第3章
-
問3.1
- ユークリッド距離。
-
問3.2
- (a) $rms(x)=\sqrt{\frac{n(rms(a))^2+m(rms(b))^2}{n+m}}$
- (b) $avg(x)=\frac{\sqrt{n^2(avg(a))^2+m^2(avg(b))^2}}{n+m}$
-
問3.3
\begin{align}
\|a+b\|&\le\|a\|+\|b\| \\
a&=\alpha+\beta, b=-\beta と置くと \\
\|\alpha+\beta-\beta\|&\le\|\alpha+\beta\|+\|-\beta\| \\
\|\alpha+\beta\|&\ge\|\alpha\|-\|\beta\|\\
記号は任意なので入れ替えると \\
\|a+b\|&\ge\|a\|-\|b\|
\end{align}
- 問3.4
- (a)
\begin{align}
(a+b)^{\top}(a-b)&=a^{\top}a-a^{\top}b+b^{\top}a-b^{\top}b \\
&=a^{\top}a-b^{\top}b \\
&=\|a\|^2-\|b\|^2
\end{align}
-
- (b)
\begin{align}
\|a\|&=\sqrt{a^{top}a} より \\
\|a+b\|^2+\|a-b\|^2&=(a+b)^{\top}(a+b)+(a-b)^{\top}(a-b) \\
&=a^{\top}a+a^{\top}b+b^{\top}a+b^{\top}b+a^{\top}a-a^{\top}b-b^{\top}a+b^{\top}b \\
&=2a^{\top}a+2b^{\top} \\
&=2(\|a\|^2+\|b\|^2) \\
\end{align}
- 問3.5
- 1ノルム
\begin{align}
\|x\|_1 \\
非負同時性 \\
\|\alpha x\|_1&=|\alpha x_1|+\dots+|\alpha x_n| \\
&=|\alpha||x_1|+\dots+|\alpha||x_n| \\
&=|\alpha|\|x\|_1 \\
三角不等式 \\
\|x\|_1+\|y\|_1-\|x+y\|_1&=|x_1|+\dots+|x_n|+|y_1|+\dots+|y_n|-(|x_1+y_1|+\dots+|x_n+y_n|) \\
&=|x_1|+|y_1|-|x_1+y_1|+\dots+|x_n|+|y_n|-|x_n+y_n| \\
&\ge0 より \\
\|x\|_1+\|y\|_1&\ge\|x+y\|_1 \\
非負性 \\
\|x\|_1&=|x_1|+\dots+|x_n| \\
&\ge0 \\
定値性 \\
\|x\|_1&=|x_1|+\dots+|x_n| \\
各項が0以外では\|x\|_1が0にならない。
\end{align}
-
- 最大値ノルム
\begin{align}
\|x\|_\infty \\
非負同時性 \\
\|\alpha x\|_\infty&=max\{|\alpha x_1|, \dots, |\alpha x_n|\} \\
&=|\alpha|max\{|x_1|, \dots, |x_n|\} \\
&=|\alpha|\|x\|_\infty \\
三角不等式 \\
\|x\|_\infty+\|y\|_\infty-\|x+y\|_\infty&=max\{|x_1|, \dots, |x_n|\}+max\{|y_1|, \dots, |y_n|\}-max\{(|x_1+y_1|, \dots, |x_n+y_n|)\} \\
&|x|の最大値が|x_i|, |y|の最大値が|y_j|, |x+y|の最大値が|x_k+y_l|とすると \\
&=|x_i|+|y_j|-|x_k+y_l| \\
i=k, j=lのとき 与式&=0 \\
それ以外のとき 与式&\gt0 \\
\therefore \|x\|_\infty+\|y\|_\infty&\ge\|x+y\|_\infty \\
非負性 \\
\|x\|_\infty&=max\{|x_1|, \dots, |x_n|\} \\
&\ge0 \\
定値性 \\
\|x\|_\infty&=max\{|x_1|, \dots, |x_n|\} \\
&各項のうち一つでも0より大きいものがあると0にはならないので \\
\|x\|_\infty&=0であれば全要素が0。
\end{align}
- 問3.6
\begin{align}
f(x)&=\|x\| \\
\hat{f}(x)&=a^{\top}(x-2)+b \\
\hat{f}(x)&=f(z)+\frac{\partial f(z)}{\partial x_1}(x_1-z_1)+\dots+\frac{\partial f(z)}{\partial x_n}(x_n-z_n) \\
f(x)&=\|x\| \\
&=\sqrt{x_1^2+\dots+x_n^2} \\
\frac{\partial f}{\partial x_i}&=\frac{\partial\sqrt{x_1+\dots+x_n}}{\partial x_i} \\
&=\frac{2x_i}{2\sqrt{\dots}} \\
&=\frac{x_i}{\sqrt{\dots}} \\
&=\frac{x_i}{\|x\|} \\
\hat{f}(x)&=\|z\|+\frac{z_1}{\|z\|}(x_1-z_1)+\dots+\frac{z_n}{\|z\|}(x_n-z_n) \\
&=\|z\|+\frac{1}{\|z\|}z^\top(x-z) \\
&=\frac{z^\top}{\|z\|}(x-z)+\|z\|
\end{align}
- 問3.7
\begin{align}
&k個の要素が|x_i|\ge a \\
&(a>0)を満たすならば \\
\|x\|^2&=x_1^2+\dots+x_n^2\ge ka^2 \\
rms(x)&=\frac{\|x\|}{\sqrt{100}}=1 \\
\|x\|&=10 \\
|x_i|&\ge 3ならば \\
10^2&\ge 10^3 k \\
k&\le \frac{100}{9}=11.\dot{1} \\
&よって最大11個 \\
\end{align}
残り2つは出来ておらず。
- 問3.8
出来ておらず。
- 問3.9
\begin{align}
f(x)&=\|x-c\|^2-\|x-d\|^2 \\
&=\|x\|^2-2x^{\top}c+\|c\|^2-(\|x\|^2-2x^{\top}d+\|d\|^2)\\
&=2x^{top}(c-d)+\|c\|^2-\|d\|^2\\
&ここで\\
a&=2(c-d)\\
b&=\|c\|^2-\|d\|^2\\
と置くと\\
f(x)&=a^{\top}x+bの形に出来るからアフィン関数である。
\end{align}
- 問3.10
- 戦没将校記念日。妥当。
- 問3.11
- 類似の属性症例の患者の可能性が高いので、誤った診断がないかの確認または、入院させるならば近しい部屋にする等の使い道が考えられる。
- 問3.12
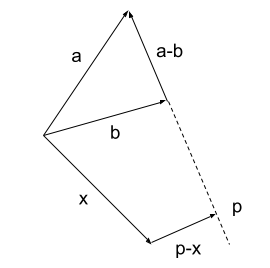
\begin{align}
\|(1-\theta)a+\theta b-x\|^2\\
f(\theta)&=(1-\theta)^2\|a\|^2+2(1-\theta)\theta a^{\top}b-2(1-\theta)a^{\top}x\\
&\quad +\theta^2\|b\|^2-2\theta b^{\top}x+\|x\|^2 \\
f'(x)&=2(1-\theta)(-1)\|a\|^2-2\theta a^{\top}b\\
&\quad 2(1-\theta)a^{\top}b+2\theta a^{\top}x\\
&\quad 2\theta\|b\|^2-2b^{\top}x\\
&=2(\|a\|^2-2a^{\top}b+\|b\|^2)\theta-2(\|a\|^2-a^{\top}b-a^{\top}x-b^{\top}x)=0\\
\theta&=\frac{\|a\|^2-a^{\top}b-(a^{\top}-b^{\top})x}{\|a\|^2-2a^{\top}b+\|b\|^2}\\
となったが自信がない。
\end{align}
- 問3.13
\begin{align}
y&=(\max(x_1, 0), \max(x_2, 0), \dots, \max(x_n, 0))\\
z&=y-x\\
&=(y_1-x_1, y_2-x_2, \dots, y_n-x_n)\\
&=(\max(x_1, 0)-x_1, \max(x_2, 0)-x_2, \dots, \max(x_n, 0)-x_n)\\
\end{align}
\max(x_i, 0)-x_1 = \left\{
\begin{array}{ll}
|x_i| & x_i<0のとき\\
0 & x_i \ge 0のとき
\end{array}
\right. \\
よってz=y-xは非負。
\begin{align}
z^{\top}y&=(y_1-x_1)y_1+(y_2-x_2)y_2+\dots+(y_n-x_n)y_n\\
x_i<0のとき\\
y_i&=0, z_i=|x_i|\\
x_i\ge0のとき\\
y_i&=|x_i|, z_i=0\\
よって常にz^{\top}y&=0
\end{align}
- 問3.14 ご指摘いただき訂正
min{(|x-e_i|)}となるiを探すと考えると\\
|x-e_i|=\sqrt{(x_1-0)^2+\cdots+(x_i-1)^2+\cdots+(x_n-0)^2} より\\
x_iが最大となるiの要素が1の単位ベクトルe_iが\\
求める標準単位ベクトルとなる。\\
- 問3.15
\begin{align}
std&=\sqrt{\frac{(x_1-avg(x))^2+\dots+(x_n-avg(x))^2}{n}}\\
avg&=\frac{\|x\|}{\sqrt{n}}\\
&(3.5)より、\\
rms(x)^2&=avg(x)^2+std(x)^2\\
rms(x)&=\sqrt{avg(x)^2+std(x)^2}\\
std(x)^2&\ge0だから\\
rms(x)&\ge |avg(x)|\\
std(x)&=0つまりxが一定のとき等号が成り立つ。\\
同様に\\
rms(X)&\ge std(x)\\
avg(x)&=0のとき等号が成り立つ。
\end{align}
- 問3.16
- (a)
\begin{align}
avg(\alpha x+\beta \mathbf{1})&=\frac{\alpha x_1+\beta+\dots+\alpha x_n+\beta}{n}\\
&=\alpha\frac{x_1+\dots+x_n}{n}+\beta\\
&=\alpha avg(x)+\beta\\
\end{align}
-
- (b)
\begin{align}
std(\alpha x+\beta \mathbf{1})&=\sqrt{\frac{(\alpha x_1+\beta-avg(x))^2+\dots+(\alpha x_n+\beta-avg(x))^2}{n}}\\
&=\sqrt{\frac{(\alpha x_1+\beta-\alpha avg(x)-\beta)^2+\dots+(\alpha x_n+\beta-\alpha avg(x)-\beta)^2}{n}}\\
&=|\alpha|\sqrt{\frac{(x_1-avg(x))^2+\dots+(x_n-avg(x))^2}{n}}\\
&=|\alpha|std(x)
\end{align}
- 問3.17
- (a)
\begin{align}
avg(z)&=\frac{a_1 x_1+\dots+a_k x_k}{k}\\
&=a_1\frac{x_1}{k}+\dots+a_k\frac{x_k}{k}\\
&=a_1avg(x_1)+\dots+a_n avg(x_k)\\
\end{align}
-
- (b)
\begin{align}
std(z)&=\sqrt{\frac{(z_1-avg(z))^2+\dots+(z_k-avg(z))^2}{n}}\\
&=\sqrt{\frac{(a_1x_1-avg(ax))^2+\dots+(a_k x_k-avg(ax))^2}{n}}\\
&=\sqrt{\frac{a_1^2(x_1-avg(x))^2+\dots+a_k^2(x_k-avg(x))^2}{n}}\\
&=\sqrt{a_1^2std(x_1)^2+\dots+a_k^2std(x_k)^2}
\end{align}
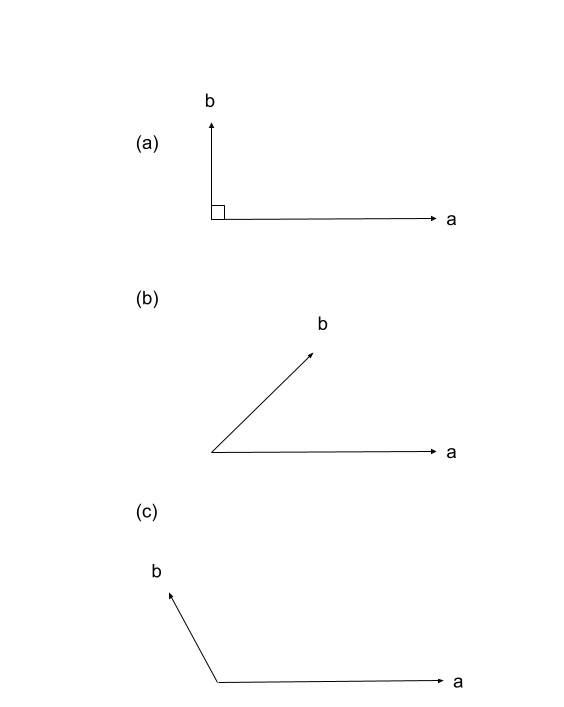
- 問3.18
\begin{align}
&(3.6)より、\\
(左辺)^2&=\|a\|^2+\|b\|^2+2\|a\|\|b\|cos\theta \quad(a, bのなす角を\thetaとする)\\
(右辺)^2&=\|a\|^2+2\|a\|\|b\|+\|b\|^2\\
よってcos\theta&=0つまり\theta=0のとき与式は成り立つ。\\
つまりaとbが同じ方向上で同じ向きのとき与式は成り立つ。
\end{align}
- 問3.19
- (a)
\begin{align}
&(3.6)より、\\
(左辺)^2&=\|x\|^2+2\|x\|\|y\|\cos\theta+\|y\|^2 \\
&=2\|x\|\|y\|\cos\theta+(右辺)^2 \\
(左辺)^2&=(右辺)^2 より \\
2\|x\|\|y\|\cos\theta&=0 \\
つまりa\perp b\\
また逆にa\perp bならば\\
(左辺)&=(右辺)
\end{align}
-
- (b)
\begin{align}
(左辺)^2&>(右辺)^2 \\
2\|a\|\|b\|\cos\theta&>0\\
つまり0&<\theta<\frac{\pi}{2}\\
逆に0&<\theta<\frac{\pi}{2}のとき\\
(左辺)^2&>(右辺)^2 つまり\|a\|\|b\|>\sqrt{\|a\|^2\|b\|^2}\\
\end{align}
-
- (c)
\begin{align}
同様に、\\
2\|a\|\|b\|\cos\theta&<0 \\
つまり\frac{\pi}{2}&<\theta<\pi\\
逆も同様
\end{align}
- 問3.20
- 分からず。
- 問3.21
- (a)$$D(x)=\Sigma_{i=2}^{T}{(x_{i-1}-x_i)^2}$$
- (b)$$\min{D(x)}=0$$ 信号が一定で変化がない時。
- (c)$$|x_i|\le 1$$
- $$\max{D_x}=4(T-1)$$
- 問3.22
- 北京の座標ベクトルをa, パルアルトの座標ベクトルをbとおくと、
- $$a=(R\sin{116.392^\circ}\cos{39.914^\circ}, R\cos{116.392^\circ}\cos{39.914^\circ}, R\sin{39.914^\circ})$$
- $$b=(R\sin{-122.138^\circ}\cos{37.429^\circ}, R\cos{-122.138^\circ}\cos{37.429^\circ}, R\sin{37.429^\circ})$$
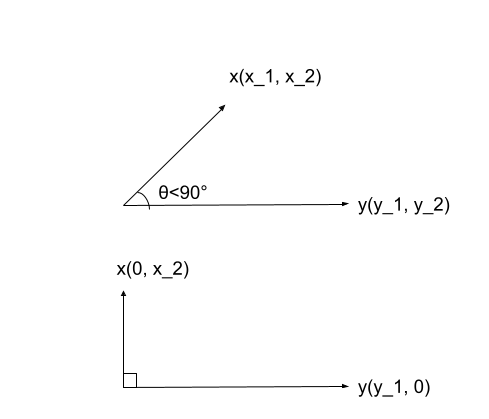
- 問3.23
\begin{align}
x\cdot y&=|x||y|\cos{\theta} (\thetaはxとyがなす角) \\
\cos{\theta}&=\frac{x\cdot y}{|x||y|} \\
&=\frac{x_1 y_1+\dots+x_n y_n}{\sqrt{x_1^2+\dots+x_n^2}\sqrt{y_1^2+\dots+y_n^2}} \\
&\ge0 より\\
-90^\circ&\le\theta\le90^\circ だが\\
\thetaの定義により正に取れるので\\
0&\le\theta\le90^\circ\\
\end{align}
\begin{align}
x_1 y_1+x_2 y_2=0 より\\
x_1かy_1が0かつx_2かy_2が0のとき\theta=90^\circ\\
つまりxとyは直行する。
\end{align}
- 問3.24
- (a)
\begin{align}
x&:(1, 0) \\
z_1&:(0, 1) \\
z_2&:(2, 2) \\
\|x-z_1\|&=\sqrt{1+1}=\sqrt{2}\\
\|x-z_2\|&=\sqrt{1+4}=\sqrt{5}\\
\|x-z_1\|&<\|x-z_2\|より\\
z_1が距離最近傍\\
\cos{\theta_1}&=\frac{x\cdot z_1}{\|x\|\|z_1\|}=0\\
\theta_1&=90^\circ\\
\cos{\theta_2}&=\frac{x\cdot z_2}{\|x\|\|z_2\|}=\frac{1}{\sqrt{2}} \\
\theta_2&=45^\circ\\
\therefore z_2が角度最近傍
\end{align}
-
- (b)
\begin{align}
距離最近傍のzをz_j\\
角度最近傍のzをz_kとおく\\
j\ne k\\
\|x-z_j\|&<\|z-z_l\|\quad (j\ne l)\\
\frac{x\cdot z_k}{\|x\|\|z_k\|}&>\frac{x\cdot z_l}{\|x\|\|z_l\|}\quad (k\ne l) \\
\|z_i\|&=1より\\
x\cdot z_k&>x\cdot z_l\\
x_1z_{k_1}+x_2z_{k_2}&<x_1z_{l_1}+x_2z_{l_2}\\
x_1(z_{l_1}-z_{k_1})+x_2(z_{l_2}-z_{k_2})&>0 \\
\sqrt{(x-z_j)^2}&<\sqrt{(x-z_l)^2} \\
\sqrt{x^2-2z_jx+z_j^2}&<\sqrt{x^2-2z_lx+z_l^2}\\
\sqrt{x^2-2z_jx}&<\sqrt{x^2-2z_lx}\\
両辺の2乗\\
x^2-2z_jx&<x^2-2z_lx \\
z_jx&>z_lx \\
jとkが異なるのは矛盾。よってj=kより\\
距離最近傍と角度最近傍は一致する
\end{align}
- 問3.25
- (a)
\begin{align}
E[p]&=\theta_E[r]+(1-\theta)\mu^{rf}\mathbf{1} \\
&=\theta\mu+(1-\theta)\mu^{rf}\mathbf{1}\\
std[p]&=\theta_{std}[r]+r\{(1-\theta)\mu^{rf}\mathbf{1}\} \\
&=\theta\sigma\\
\theta&=0のとき\\
E[p]&=\mu^{rf}\mathbf{1} \\
std[p]&=0 \quad 現金のみなので平均、分散とも合致\\
\theta&=1のとき\\
E[p]&=\mu\\
std[p]&=\sigma \quad 資産のみなので平均、分散とも合致\\
\end{align}
-
- (b)
\begin{align}
\theta\sigma&=\sigma^{tar} より\\
\theta&=\frac{\sigma^{tar}}{\sigma}
\end{align}
-
- (c)
\begin{align}
レバレッジをするのは\theta&>1のときだから \\
\frac{\sigma^{tar}}{\sigma}&>1つまり\sigma<\sigma^{tar}のとき\\
空売りをするのは\theta&<0のときだから\\
\frac{\sigma^{tar}}{\sigma}&<0はあり得ない\\
ヘッジをするのは0&\le\theta\le1のときだから\\
0&\le\frac{\sigma^{tar}}{\sigma}\le1つまり \\
\sigma&\ge\sigma^{tar}のとき
\end{align}
- 問3.27
\begin{align}
xの平均除去ベクトルを\\
\tilde{x} &=\mathbf{x}-\mathrm{avg}(x)\mathbf{1} とする\\
\mathrm{MSD}(\tilde{x})&=\frac{1}{n^2}\Sigma{(\tilde{x_i}-\tilde{x_j})}\\
&=\frac{1}{n^2}\Sigma{\{(x_i-\mu)-(x_j-\mu)\}^2}\\
&=\frac{1}{n^2}\Sigma{(x_i-x_j)^2}\\
&=\mathrm{MSD}(x) \\
ううむ、ここまで
\end{align}
- 問3.28
\tilde{x}=(x_1\sqrt{w_1}, \cdots, x_n\sqrt{w_n}) \\
\tilde{y}=(y_1\sqrt{w_1}, \cdots, y_n\sqrt{w_n}) \\
|a^{\top}b|\le\|a\|\|b\|\\
\tilde{x}, \tilde{y}に対してコーシー・シュワルツの不等式より\\
|\tilde{x}^\top\tilde{y}|\le\|\tilde{x}\|\|\tilde{y}\|\\
よって\\
|w_1x_1y_1+\cdots+w_nx_ny_n|\le\|x_n\|_w\|y_n\|_w