訳注
http://topepo.github.io/caret/preprocess.html の和訳です。
図は訳者がRで再現を試みたものです。
日本語としておかしいと思われるところやや改訳しました。
caret には説明変数の前処理のための関数がいくつかあります。すべてのデータが数値であるとみなします(すなわち、ファクター型(factors)は model.matrix、dummyVars あるいは別の手法でダミー変数に変換します)。
3.1 ダミー変数の作成
dummyVars 関数は1つあるいは1つ以上のファクター型(factors)からダミー変数の(less than full rank parameterized)セットを生成します。この関数は予測式とデータセットと目的変数からダミー変数を作成します。
例えば、earth パッケージの etitanic データセットには2つのファクター型(factors)があります:pclass1 (with levels 1st, 2nd, 3rd) と sex (with levels female, male)。base R の model.matrix 関数はは以下の変数を作成します:
library(earth)
data(etitanic)
head(model.matrix(survived ~ ., data = etitanic))
(Intercept) pclass2nd pclass3rd sexmale age sibsp parch
1 1 0 0 0 29.0000 0 0
2 1 0 0 1 0.9167 1 2
3 1 0 0 0 2.0000 1 2
4 1 0 0 1 30.0000 1 2
5 1 0 0 0 25.0000 1 2
6 1 0 0 1 48.0000 0 0
dummyVars を使う場合は:
dummies <- dummyVars(survived ~ ., data = etitanic)
head(predict(dummies, newdata = etitanic))
pclass.1st pclass.2nd pclass.3rd sex.female sex.male age sibsp parch
1 1 0 0 1 0 29.0000 0 0
2 1 0 0 0 1 0.9167 1 2
3 1 0 0 1 0 2.0000 1 2
4 1 0 0 0 1 30.0000 1 2
5 1 0 0 1 0 25.0000 1 2
6 1 0 0 0 1 48.0000 0 0
【訳注:すみませんわかりません】
切片の値がなく、個々のファクター型(factor)が個々のレベルのダミー変数を持つような場合は、このパラメータ化は幾つかのモデル関数では有効ではありません、例えば lm のような。
Note there is no intercept and each factor has a dummy variable for each level, so this parameterization may not be useful for some model functions, such as lm.
3.2 分散がゼロあるいはほぼゼロの説明変数
説明変数の値がただ1つの値となる場合がある(すなわち、分散が0の説明変数)。(tree-basedモデル以外の)多くのモデルでは、モデルがクラッシュし、安定に最適化しなくなります。
同様に、説明変数の値が極めて少ない頻度しかない場合があります。例えば、薬剤抵抗性のデータの説明変数 nR11 (11員環の数)データは少ない値しか取らず、とてもアンバランスです:
data(mdrr)
data.frame(table(mdrrDescr$nR11))
Var1 Freq
1 0 501
2 1 4
3 2 23
ここでの注意すべきことは、クロスバリデーション・ブートストラップによりサンプルをサブサンプルに分けるとき、説明変数の分散が0となることです。「分散がほぼ0」の説明変数を同定しモデルから取り除くことが必要です。
説明変数のこれらの特徴を同定することは、以下の2つの方法で計算できます:
- 2番目に多い値に対する最も多い値の頻度(「頻度比」("frequency ratio")と呼ばれる)、例えばよく動く説明変数がほぼ1つであったり、とてもアンバランスなデータの場合に、
- 「ユニークな値の割合」すなわち、ユニークな値の数をサンプルの総数で割った値(×100)は、データが増加すると0に近づいていきます。
もし頻度比(frequency ratio)が事前に設定した値より小さく、ユニークな値の割合が閾値より小さい場合は、分散がほぼ0となる説明変数であるとみなします。
離散一様分布(訳注:サイコロの出目のようなもの)データのような平らに分布しているのに低い粒度のデータと誤って同定することは避けたいものです。2つの基準を用いることにより、そのような説明変数を誤って判断することを避けます。
MDRRデータを使って、nearZeroVar 関数が分散がほぼ0の変数(saveMetrics 属性を使い詳細を確認できますがデフォルトでは FALSE です)を同定できることを確認しよう:
nzv <- nearZeroVar(mdrrDescr, saveMetrics= TRUE)
nzv[nzv$nzv,][1:10,]
freqRatio percentUnique zeroVar nzv
nTB 23.00000 0.3787879 FALSE TRUE
nBR 131.00000 0.3787879 FALSE TRUE
nI 527.00000 0.3787879 FALSE TRUE
nR03 527.00000 0.3787879 FALSE TRUE
nR08 527.00000 0.3787879 FALSE TRUE
nR11 21.78261 0.5681818 FALSE TRUE
nR12 57.66667 0.3787879 FALSE TRUE
D.Dr03 527.00000 0.3787879 FALSE TRUE
D.Dr07 123.50000 5.8712121 FALSE TRUE
D.Dr08 527.00000 0.3787879 FALSE TRUE
dim(mdrrDescr)
[1] 528 342
nzv <- nearZeroVar(mdrrDescr)
filteredDescr <- mdrrDescr[, -nzv]
dim(filteredDescr)
[1] 528 297
デフォルトでは、nearZeroVar は疑いのあるフラグを変数の位置に付与して返します。
3.3 相関する説明変数の同定
(pls のような)相関する説明変数で精度が良くなるモデルがある一方で、説明変数の相関レベルを減らしたほうが良くなるモデルもあります。
相関行列が与えられたとき、 findCorrelation 関数により、どの説明変数を削るかのフラグを得ます:
descrCor <- cor(filteredDescr)
highCorr <- sum(abs(descrCor[upper.tri(descrCor)]) > .999)
前の MDRR データでは、65の説明変数がほぼ完全に相関しており(|相関係数| > 0.999)、すなわち、total information index of atomic composition (IAC) や total information content index (neighborhood symmetry of 0-order) (TIC0)(相関係数=1)のようなものである。次の例では、相関係数の絶対値が0.75より大きい説明変数を取り除いた効果を示している。
descrCor <- cor(filteredDescr)
summary(descrCor[upper.tri(descrCor)])
Min. 1st Qu. Median Mean 3rd Qu. Max.
-0.99610 -0.05373 0.25010 0.26080 0.65530 1.00000
highlyCorDescr <- findCorrelation(descrCor, cutoff = .75)
filteredDescr <- filteredDescr[,-highlyCorDescr]
descrCor2 <- cor(filteredDescr)
summary(descrCor2[upper.tri(descrCor2)])
Min. 1st Qu. Median Mean 3rd Qu. Max.
-0.70730 -0.05378 0.04418 0.06692 0.18860 0.74460
3.4 線形依存性
findLinearCombos 関数は、線形の組み合わせ(もし存在するのなら)を数え上げたい行列のQR分解に用いられる。例えば、フルランクでない次の行列を考えるとき:
ltfrDesign <- matrix(0, nrow=6, ncol=6)
ltfrDesign[,1] <- c(1, 1, 1, 1, 1, 1)
ltfrDesign[,2] <- c(1, 1, 1, 0, 0, 0)
ltfrDesign[,3] <- c(0, 0, 0, 1, 1, 1)
ltfrDesign[,4] <- c(1, 0, 0, 1, 0, 0)
ltfrDesign[,5] <- c(0, 1, 0, 0, 1, 0)
ltfrDesign[,6] <- c(0, 0, 1, 0, 0, 1)
(訳注:上記例を実行すると転置されて1列目がすべて1となる行列となる)。2列目と3列目を足したものが1列目と等しくなっています。同様に、4列目、5列目、6列目を足すと1列目に等しく。findLinearCombos はこれらの依存性を調べて返します。それぞれの線形の組み合わせにおいて、依存性が取り除ける限り取り除きます。findLinearCombos は、線形依存性があり取り除くべき列の位置をベクトルで返します:
comboInfo <- findLinearCombos(ltfrDesign)
comboInfo
$linearCombos
$linearCombos[[1]]
[1] 3 1 2
$linearCombos[[2]]
[1] 6 1 4 5
$remove
[1] 3 6
ltfrDesign[, -comboInfo$remove]
[,1] [,2] [,3] [,4]
[1,] 1 1 1 0
[2,] 1 1 0 1
[3,] 1 1 0 0
[4,] 1 0 1 0
[5,] 1 0 0 1
[6,] 1 0 0 0
このような依存性は、分子構造を示す二値の化学的フィンガープリントのような大きなデータの時に発生します。
3.5 preProcess 関数
preProcess クラスは値のセンタリング(訳注、平均を0にする)やスケーリング(訳注、分散を1にする)などを行います。 preProcess はそれぞれの操作に必要なパラメータを評価し、predict.preProcess はそれらを実際のデータに適用します。この関数は train 関数を呼び出すときのインターフェースの関数ともなっています。
訳注:説明変数間での比較が出来るように平均と分散を合わせるためにセンタリングやスケーリングを行う。基準を合わせればよいので0や1の必然性はないがたいていは平均を0、分散を1とする。
次のいくつかの節で紹介するテクニックは、複数の手法をどのように用いるかです。注目すべき点は、 preProcess 関数は(例えばトレーニングデータセットのような)特定のデータだけではなくすべてのデータにおいて、再計算することなく評価を行っていることです。
(訳注:一度前処理をしたら、予測の再計算の時も前処理はキャッシュを使うなどで再計算を行わないとのことか?)
3.6 センタリングとスケーリング
以下の例では、MDRR データの半分を説明変数の値とスケーリングの評価に用いています。preProcess 関数は実際に前処理を行うわけではありません。 predict.preProcess が前処理を行います。
set.seed(96)
inTrain <- sample(seq(along = mdrrClass), length(mdrrClass)/2)
training <- filteredDescr[inTrain,]
test <- filteredDescr[-inTrain,]
trainMDRR <- mdrrClass[inTrain]
testMDRR <- mdrrClass[-inTrain]
preProcValues <- preProcess(training, method = c("center", "scale"))
trainTransformed <- predict(preProcValues, training)
testTransformed <- predict(preProcValues, test)
preProcess の"ranges"オプションは値を[0, 1](訳注:0以上、1以下)の範囲に収めます。
3.7 インピューテーション Imputation
(訳注:impute, imputationをどう訳していいかわかりませんでした。片仮名のままインピューテーションでいいのだろうか。あるデータだけから欠損値のデータを推定する、みたいな意味ですよね。)
preProcess はトレーニングセットの情報だけに基づいてデータセットを impute しようとします。1つの方法はK近傍法です。任意のサンプルにより、K番目までの近傍のデータをトレーニングセットで見つけ、その値(例えば平均値)をimputeに用います。この手法では preProcess は自動的にセンタリングとスケーリングを行います。一方 bagged tree でも impute が出来ます。データの予測因子にそれぞれについて、トレーニングセットの他の説明変数のすべてを使って bagged tree が生成されます。新しいサンプルの説明変数に欠損値があった場合に bagged モデルはその値を予測します。理論的にはこの方法はより強力な imputing 手法でありますが、近傍法よりも計算コストが大きくなります。
3.8 説明変数の変換(訳注:次元削減のような)Transforming Predictors
主成分分析(PCA)で次元削減する必要がある場合に、新しい(変換後の)変数は他の変数と相関がなくなります。 preProcess クラスではこの "pca" を含む変換を属性に指定出来ます。この場合説明変数を強制的にスケーリングします。PCA が指定された場合は、 predict.preProcess はカラム名を PC1, PC2 と変えます。
似た手法で、独立成分分析(ICA)が、各成分が独立(PCA が無相関となるのに対して)となったものの線形結合となるように変数を変換することに用いられています。変換後の新たな変数は IC1, IC2 となります。
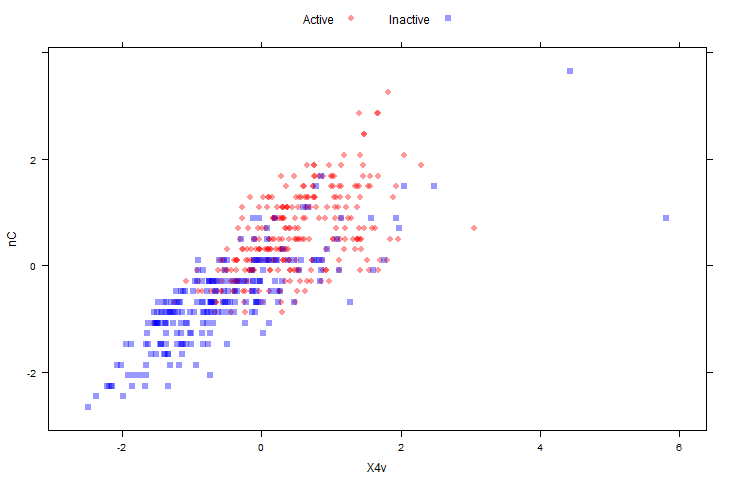
"spatial sign"(訳注:空間分布?) 変換 (Serneels et al, 2006) は p次元の単位円への説明変数の投影としてデータを取り扱う。ここでのpは説明変数の数である。下記2図では MDRR データのセンタリングとスケーリングされた説明変数について、 spatial sign 変換する前とした後を示している。センタリングとスケーリングはこの変換をする前に済ませてある。
library(AppliedPredictiveModeling)
transparentTheme(trans = .4)
plotSubset <- data.frame(scale(mdrrDescr[, c("nC", "X4v")]))
xyplot(nC ~ X4v,
data = plotSubset,
groups = mdrrClass,
auto.key = list(columns = 2))
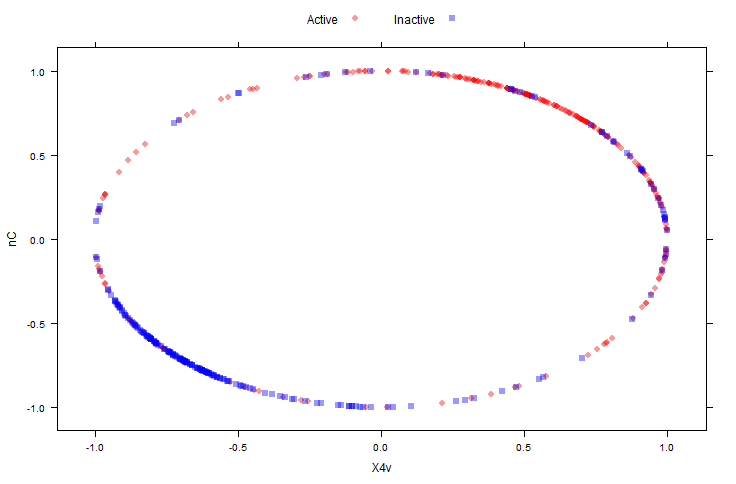
spatial sign 実施後:
transformed <- spatialSign(plotSubset)
transformed <- as.data.frame(transformed)
xyplot(nC ~ X4v,
data = transformed,
groups = mdrrClass,
auto.key = list(columns = 2))
別のオプション、"BoxCox" では、データが0より大きい場合にボックスコックス変換を行います。
preProcValues2 <- preProcess(training, method = "BoxCox")
trainBC <- predict(preProcValues2, training)
testBC <- predict(preProcValues2, test)
preProcValues2
Created from 264 samples and 31 variables
Pre-processing:
- Box-Cox transformation (31)
- ignored (0)
Lambda estimates for Box-Cox transformation:
Min. 1st Qu. Median Mean 3rd Qu. Max.
-2.0000 -0.2000 0.3000 0.4097 1.7000 2.0000
NA 値が変換できなかった説明変数を示します。この変換ではデータの値が0より大きいことが必須です。2つの似た手法、 Yeo-Johnson と exponential transformation of Manly (1976) も preProcess で行えます。
3.9 すべてを1つにまとめると
予測モデル構築のケーススタディを行いましょう。高性能のコンピュータ環境での実行時間を予測するものです。データは:
library(AppliedPredictiveModeling)
data(schedulingData)
str(schedulingData)
'data.frame': 4331 obs. of 8 variables:
$ Protocol : Factor w/ 14 levels "A","C","D","E",..: 4 4 4 4 4 4 4 4 4 4 ...
$ Compounds : num 997 97 101 93 100 100 105 98 101 95 ...
$ InputFields: num 137 103 75 76 82 82 88 95 91 92 ...
$ Iterations : num 20 20 10 20 20 20 20 20 20 20 ...
$ NumPending : num 0 0 0 0 0 0 0 0 0 0 ...
$ Hour : num 14 13.8 13.8 10.1 10.4 ...
$ Day : Factor w/ 7 levels "Mon","Tue","Wed",..: 2 2 4 5 5 3 5 5 5 3 ...
$ Class : Factor w/ 4 levels "VF","F","M","L": 2 1 1 1 1 1 1 1 1 1 ...
データはカテゴリカルデータと数値データが混じったものです。連続値の説明変数については Yeo-Johnson 変換を行い、続けてセンタリングとスケーリングを行いたくなります。木のモデルも実施してみましょう、ただファクター型(factors)はファクターのままとします(ダミー変数を作ります)。最後の列を除き次のように実行します。
pp_hpc <- preProcess(schedulingData[, -8],
method = c("center", "scale", "YeoJohnson"))
pp_hpc
Created from 4331 samples and 7 variables
Pre-processing:
- centered (5)
- ignored (2)
- scaled (5)
- Yeo-Johnson transformation (5)
Lambda estimates for Yeo-Johnson transformation:
-0.08, -0.03, -1.05, -1.1, 1.44
transformed <- predict(pp_hpc, newdata = schedulingData[, -8])
head(transformed)
Protocol Compounds InputFields Iterations NumPending Hour Day
1 E 1.2289589 -0.6324538 -0.06155877 -0.554123 0.004586502 Tue
2 E -0.6065822 -0.8120451 -0.06155877 -0.554123 -0.043733215 Tue
3 E -0.5719530 -1.0131509 -2.78949011 -0.554123 -0.034967191 Thu
4 E -0.6427734 -1.0047281 -0.06155877 -0.554123 -0.964170760 Fri
5 E -0.5804710 -0.9564501 -0.06155877 -0.554123 -0.902085029 Fri
6 E -0.5804710 -0.9564501 -0.06155877 -0.554123 0.698108779 Wed
"ignored" が2つの説明変数についていますが、ファクター型の説明変数です。これらは変換されませんが連続値の説明変数は変換されます。しかし、number of pending jobs(訳注:NumPending)はとても疎でアンバランスな分布となっています:
mean(schedulingData$NumPending == 0)
[1] 0.7561764
別のモデルでは、これは少し問題となります(特にリサンプルかダウンサンプルをする場合に)。 分散が0あるいはほぼ0をチェックするフィルタを付け加えることが出来ます:
pp_no_nzv <- preProcess(schedulingData[, -8],
method = c("center", "scale", "YeoJohnson", "nzv"))
pp_no_nzv
Created from 4331 samples and 7 variables
Pre-processing:
- centered (4)
- ignored (2)
- removed (1)
- scaled (4)
- Yeo-Johnson transformation (4)
Lambda estimates for Yeo-Johnson transformation:
-0.08, -0.03, -1.05, 1.44
predict(pp_no_nzv, newdata = schedulingData[1:6, -8])
Protocol Compounds InputFields Iterations Hour Day
1 E 1.2289589 -0.6324538 -0.06155877 0.004586502 Tue
2 E -0.6065822 -0.8120451 -0.06155877 -0.043733215 Tue
3 E -0.5719530 -1.0131509 -2.78949011 -0.034967191 Thu
4 E -0.6427734 -1.0047281 -0.06155877 -0.964170760 Fri
5 E -0.5804710 -0.9564501 -0.06155877 -0.902085029 Fri
6 E -0.5804710 -0.9564501 -0.06155877 0.698108779 Wed
"removed" が1つの説明変数についていますが疎なデータを除去するものです。
3.10 クラス距離の計算
クラス重心の距離に基づき(線形分離がどう効くか似ている)、新たな説明変数を生成する関数が caret にはあります。ファクター型変数のそれぞれのレベルについて、クラス重心と共分散行列を計算します。新しいサンプルが追加されたとき、クラス重心からのマハラノビス距離を計算し、説明変数に追加します。これは非線形モデルにおいて、判別境界が実際は線形な場合に役に立ちます。
サンプル数よりも1つのクラスの説明変数が多い場合には、 classDist 関数に pca 属性をつけて主成分分析をするようにすると、1つの共分散行列に集約されてしまうという問題を避けることが出来ます。
predict.classDist はクラス距離を生成します。デフォルトでは、距離は対数値ですが trans 属性を predict.classDist とすることで変更できます。
例では、 MDDR データを用いています。
centroids <- classDist(trainBC, trainMDRR)
distances <- predict(centroids, testBC)
distances <- as.data.frame(distances)
head(distances)
dist.Active dist.Inactive
PROMETHAZINE 5.810607 4.098229
ACEPROMETAZINE 4.272003 4.169292
PYRATHIAZINE 4.570192 4.224053
THIORIDAZINE 4.548315 5.064125
MESORIDAZINE 4.621708 5.080362
SULFORIDAZINE 5.344699 5.145311
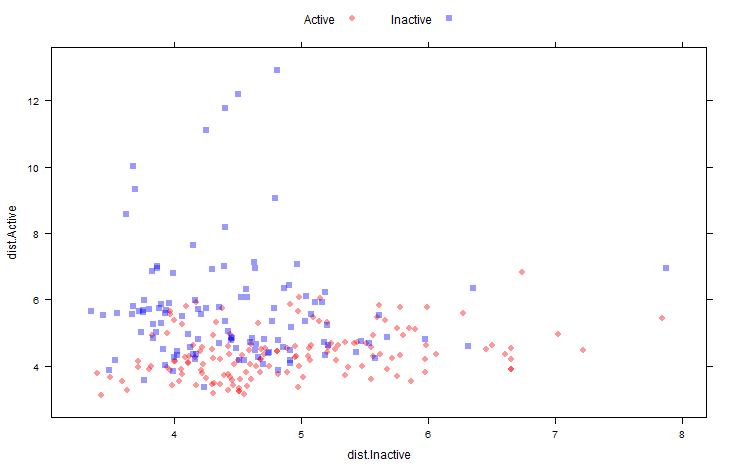
次の図では 手持ちサンプルのクラス距離行列のスキャッタープロットを示しています:
xyplot(dist.Active ~ dist.Inactive,
data = distances,
groups = testMDRR,
auto.key = list(columns = 2))