クリギング入門
- コロナ社様のサイトにて読者モニターレビューをさせていただきました。コロナ社：『クリギング入門』の「レビュー」
- 地理空間データを用いる場合の空間内挿推定手法の１つであるクリギングの分かりやすい入門書です。
- 分かりやすい本でしたが実装例がExcelのためPythonに翻訳してみました。
  - pyKrigingというクリギングのライブラリがあるようですが、今回は１ステップずつを確認しつつ検証することが目的であるためテキストのExcel計算をPythonで泥臭く１つずつ実施しています。

テキスト「6.2 Excelを用いた計算」のPythonでの実行

(1) バリオグラム推定

import pandas as pd
import numpy as np
from scipy.spatial import distance_matrix
from scipy.optimize import minimize

import matplotlib.pyplot as plt

データ入力

df = pd.DataFrame({'x': [2.0, 1.0, 4.0, 6.0, 5.5], 'y': [4.0, 3.0, 2.5, 2.0, 4.0], 'z':[5.3, 4.5, 4.6, 2.9, 3.2]})
df

    x   y   z
0   2.0 4.0 5.3
1   1.0 3.0 4.5
2   4.0 2.5 4.6
3   6.0 2.0 2.9
4   5.5 4.0 3.2

図６.６標本平均、標本分散の計算

m = df.z.mean()
m

4.1

s2 = df.z.var()
s2

1.0249999999999997

図6.7 データ間の距離の計算

df_dist = pd.DataFrame(distance_matrix(df.iloc[:, 0:2], df.iloc[:, 0:2]))
df_dist

    0           1           2           3           4
0   0.000000    1.414214    2.500000    4.472136    3.500000
1   1.414214    0.000000    3.041381    5.099020    4.609772
2   2.500000    3.041381    0.000000    2.061553    2.121320
3   4.472136    5.099020    2.061553    0.000000    2.061553
4   3.500000    4.609772    2.121320    2.061553    0.000000

図6.8 非類似度の計算

df_dissimilarity = pd.DataFrame(np.square(distance_matrix(df.iloc[:, 2:3], df.iloc[:, 2:3])) / 2)
df_dissimilarity

    0       1       2       3       4
0   0.000   0.320   0.245   2.880   2.205
1   0.320   0.000   0.005   1.280   0.845
2   0.245   0.005   0.000   1.445   0.980
3   2.880   1.280   1.445   0.000   0.045
4   2.205   0.845   0.980   0.045   0.000

図6.9 データペアの距離と非類似度の整理¹

=INDEX('データ（3）'!$D$4:$H$8,B11,C11)

df_2 = pd.DataFrame(columns = ['j', 'k', 'h', 'g'])
for j in range(len(df_dist)):
  for k in range(j + 1, len(df_dist)):
    df_2 = df_2.append({'j': j + 1, 'k': k + 1, 'h': df_dist.iloc[j, k], 'g': df_dissimilarity.iloc[j, k]}, ignore_index=True)
df_2

    j   k   h           g
0   1.0 2.0 1.414214    0.320
1   1.0 3.0 2.500000    0.245
2   1.0 4.0 4.472136    2.880
3   1.0 5.0 3.500000    2.205
4   2.0 3.0 3.041381    0.005
5   2.0 4.0 5.099020    1.280
6   2.0 5.0 4.609772    0.845
7   3.0 4.0 2.061553    1.445
8   3.0 5.0 2.121320    0.980
9   4.0 5.0 2.061553    0.045

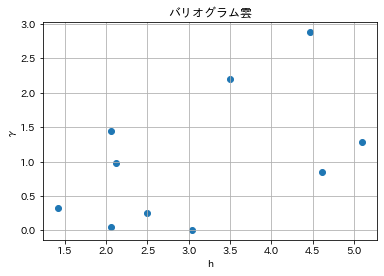
図6.10 バリオグラム雲の計算

plt.scatter(df_2.iloc[:, 2:3], df_2.iloc[:, 3:4])
plt.title("バリオグラム雲")
plt.xlabel("h")
plt.ylabel("γ")
plt.grid(True)

図6.11 ラグによるデータ間距離の分類

lag = 1
df_2['h2'] = list(map(int, df_2.h / lag))
df_2

    j   k   h           g       h2
0   1.0 2.0 1.414214    0.320   1
1   1.0 3.0 2.500000    0.245   2
2   1.0 4.0 4.472136    2.880   4
3   1.0 5.0 3.500000    2.205   3
4   2.0 3.0 3.041381    0.005   3
5   2.0 4.0 5.099020    1.280   5
6   2.0 5.0 4.609772    0.845   4
7   3.0 4.0 2.061553    1.445   2
8   3.0 5.0 2.121320    0.980   2
9   4.0 5.0 2.061553    0.045   2

図6.12 非類似度の平均化（経験バリオグラム）

df_3 = df_2.groupby('h2').mean()
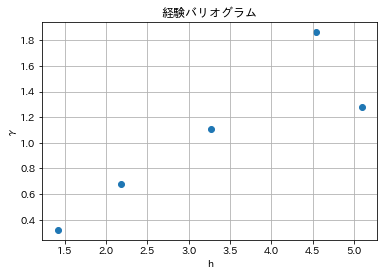
df_3

    j       k       h           g
h2              
1   1.00    2.00    1.414214    0.32000
2   2.75    4.25    2.186106    0.67875
3   1.50    4.00    3.270691    1.10500
4   1.50    4.50    4.540954    1.86250
5   2.00    4.00    5.099020    1.28000

図6.13 経験バリオグラムの作成

plt.scatter(df_3.iloc[:, 2:3], df_3.iloc[:, 3:4])
plt.title("経験バリオグラム")
plt.xlabel("h")
plt.ylabel("γ")
plt.grid(True)

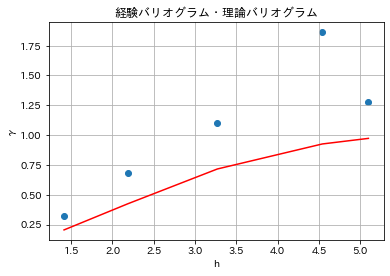
図6.14 理論バリオグラム（初期パラメータ）表示

a = 3
b = 0
c = 1.03
df_3['g2'] = b + (c - b) * (1 - np.exp((df_3.h / a) ** 2 * (-1)))
df_3

    j       k       h           g       g2
h2                  
1   1.00    2.00    1.414214    0.32000 0.205240
2   2.75    4.25    2.186106    0.67875 0.424347
3   1.50    4.00    3.270691    1.10500 0.716214
4   1.50    4.50    4.540954    1.86250 0.925814
5   2.00    4.00    5.099020    1.28000 0.972693

plt.scatter(df_3.iloc[:, 2:3], df_3.iloc[:, 3:4])
plt.plot(df_3.iloc[:, 2:3], df_3.iloc[:, 4:5], color = 'red')
plt.title("経験バリオグラム・理論バリオグラム")
plt.xlabel("h")
plt.ylabel("γ")
plt.grid(True)

図6.15 誤差2乗和の計算²

rss = sum((df_3.g - df_3.g2) ** 2)
rss

1.2008629589537976

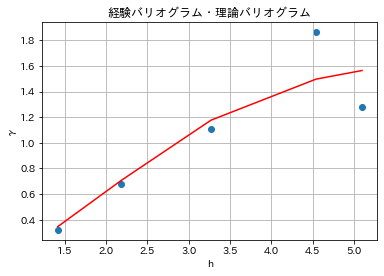
図6.16 ソルバーを用いた理論バリオグラムのパラメータ決定
図6.17 決定した理論バリオグラム

# 目的変数
def func(x):
  return sum([(df_3.g.iloc[i] - x[1] * (1 - np.exp((df_3.h.iloc[i] / x[0]) ** 2 * (-1)))) **2 for i in range(len(df_3))])

# 制約条件式
def cons(x):
  return np.array([x[0] - 2, x[1] - 1])

cons = ({'type': 'ineq', 'fun' : cons})

result = minimize(func, [3, 1.03], constraints=cons)
print(result)
a = result.x[0]
b = 0
c = result.x[1]
print(a, b, c)

     fun: 0.22117939583238733
     jac: array([ 0.00044499, -0.00123285])
 message: 'Optimization terminated successfully.'
    nfev: 29
     nit: 7
    njev: 7
  status: 0
 success: True
       x: array([2.91004696, 1.63761046])
2.910046955029522 0 1.637610456087436

# 決定した理論バリオグラム
plt.scatter(df_3.iloc[:, 2:3], df_3.iloc[:, 3:4])
plt.plot(df_3.iloc[:, 2:3], df_3.iloc[:, 5:6], color = 'red')
plt.title("経験バリオグラム・理論バリオグラム")
plt.xlabel("h")
plt.ylabel("γ")
plt.grid(True)

(2) 単純クリギング

図6.18 観測データ間の共分散行列

a = 2.91
b = 0
c = 1.64
df_cov = df_dist.copy()
for i in range(len(df_dist)):
  for j in range(len(df_dist)):
    df_cov.iloc[i, j] = c * np.exp((df_dist.iloc[i, j] / a) ** 2 * (-1))
df_cov

    0           1           2           3           4
0   1.640000    1.295007    0.783983    0.154570    0.386003
1   1.295007    1.640000    0.550109    0.076104    0.133358
2   0.783983    0.550109    1.640000    0.992838    0.963956
3   0.154570    0.076104    0.992838    1.640000    0.992838
4   0.386003    0.133358    0.963956    0.992838    1.640000

図6.２０共分散行列の逆行列計算

df_cov_inv = pd.DataFrame(np.linalg.inv(df_cov))
df_cov_inv

    0           1           2           3           4
0   1.998142    -1.383630   -0.570299   0.370644    -0.246963
1   -1.383630   1.681016    0.019621    -0.105598   0.241365
2   -0.570299   0.019621    1.453866    -0.616057   -0.348961
3   0.370644    -0.105598   -0.616057   1.232949    -0.462960
4   -0.246963   0.241365    -0.348961   -0.462960   1.133639

図6.21 推定点と観測点の座標
図6.22 推定点と観測点間の距離計算

x = 1.5
y = 3
df_simple = df.copy()
df_simple['d'] = np.sqrt((df['x'] - x) ** 2 + (df['y'] - y) ** 2)
df_simple

    x   y   z   d
0   2.0 4.0 5.3 1.118034
1   1.0 3.0 4.5 0.500000
2   4.0 2.5 4.6 2.549510
3   6.0 2.0 2.9 4.609772
4   5.5 4.0 3.2 4.123106

6.2３図推定点と観測点間の共分散行列

df_simple['B'] = c * np.exp((df_simple['d'] / a)**2 * (-1))
df_simple

    x   y   z   d           B
0   2.0 4.0 5.3 1.118034    1.414935
1   1.0 3.0 4.5 0.500000    1.592291
2   4.0 2.5 4.6 2.549510    0.761176
3   6.0 2.0 2.9 4.609772    0.133358
4   5.5 4.0 3.2 4.123106    0.220284

6.24図単純クリギングのクリギング係数計算
６.２５図出力されたクリギング係数

df_simple['w'] = np.dot(df_cov_inv, df_simple.B)
df_simple

    x   y   z   d           B           w
0   2.0 4.0 5.3 1.118034    1.414935    0.185027
1   1.0 3.0 4.5 0.500000    1.592291    0.772940
2   4.0 2.5 4.6 2.549510    0.761176    0.171927
3   6.0 2.0 2.9 4.609772    0.133358    -0.050194
4   5.5 4.0 3.2 4.123106    0.220284    -0.042750

6.2６図データの平均との残差

df_simple['za'] = df_simple['z'] - m
df_simple

    x   y   z   d           B           w           za
0   2.0 4.0 5.3 1.118034    1.414935    0.185027    1.2
1   1.0 3.0 4.5 0.500000    1.592291    0.772940    0.4
2   4.0 2.5 4.6 2.549510    0.761176    0.171927    0.5
3   6.0 2.0 2.9 4.609772    0.133358    -0.050194   -1.2
4   5.5 4.0 3.2 4.123106    0.220284    -0.042750   -0.9

6.27図推定点１における推定値

z_sk = m + sum(df_simple.w * df_simple.za)
s2_sk = c - sum(df_simple.w * df_simple.B)
cv = np.sqrt(s2_sk) / z_sk
print(z_sk, s2_sk, cv)

4.815879929438207 0.03269746133842899 0.037547529485399515

(3) 通常クリギング

df_simple = df_dist.copy()
df_simple

    0           1           2           3           4
0   0.000000    1.414214    2.500000    4.472136    3.500000
1   1.414214    0.000000    3.041381    5.099020    4.609772
2   2.500000    3.041381    0.000000    2.061553    2.121320
3   4.472136    5.099020    2.061553    0.000000    2.061553
4   3.500000    4.609772    2.121320    2.061553    0.000000

図6.28 観測点間のバリオグラム行列

a = 2.91
b = 0
c = 1.64
for i in range(len(df_simple)):
  for j in range(len(df_simple.columns)):
    df_simple.iloc[i, j] = c * (1 - np.exp((df_simple.iloc[i, j] / a) ** 2 * (-1)))
df_simple[5] = 1
df_simple = df_simple.append(pd.Series([1, 1, 1, 1, 1, 0]), ignore_index=True)
df_simple

    0           1           2           3           4           5
0   0.000000    0.344993    0.856017    1.485430    1.253997    1
1   0.344993    0.000000    1.089891    1.563896    1.506642    1
2   0.856017    1.089891    0.000000    0.647162    0.676044    1
3   1.485430    1.563896    0.647162    0.000000    0.647162    1
4   1.253997    1.506642    0.676044    0.647162    0.000000    1
5   1.000000    1.000000    1.000000    1.000000    1.000000    0

図6.29 バリオグラム行列の逆行列

df_simple_inv = pd.DataFrame(np.linalg.inv(df_simple))
df_simple_inv

    0           1           2           3           4           5
0   -1.976357   1.442380    0.562276    -0.316280   0.287981    0.129755
1   1.442380    -1.522582   -0.041257   0.252207    -0.130748   0.349919
2   0.562276    -0.041257   -1.450911   0.596036    0.333855    -0.047786
3   -0.316280   0.252207    0.596036    -1.097284   0.565320    0.323801
4   0.287981    -0.130748   0.333855    0.565320    -1.056408   0.244310
5   0.129755    0.349919    -0.047786   0.323801    0.244310    -0.867162

図6.30 観測点と推定点間のバリオグラム行列

df_simple_2 = df.copy()
_0 = 1.5
y_0 = 3
df_simple_2['h'] = np.sqrt((df_simple_2['x'] - x_0) ** 2 + (df_simple_2['y'] - y_0) ** 2)
df_simple_2['B'] = c * (1 - np.exp((df_simple_2['h'] / a) ** 2 * (-1)))
s_no_name = pd.Series([1], index=['B'])
s_no_name
df_simple_2 = df_simple_2.append(s_no_name, ignore_index=True)
df_simple_2

    x   y   z   h           B
0   2.0 4.0 5.3 1.118034    0.225065
1   1.0 3.0 4.5 0.500000    0.047709
2   4.0 2.5 4.6 2.549510    0.878824
3   6.0 2.0 2.9 4.609772    1.506642
4   5.5 4.0 3.2 4.123106    1.419716

図６.31 通常クリギングのクリギング係数計算

df_simple_2['w'] = np.dot(df_simple_inv, df_simple_2['B'])
df_simple_2

    x   y   z   h           B           w
0   2.0 4.0 5.3 1.118034    0.225065    0.180233
1   1.0 3.0 4.5 0.500000    0.047709    0.760010
2   4.0 2.5 4.6 2.549510    0.878824    0.173693
3   6.0 2.0 2.9 4.609772    1.506642    -0.062158
4   5.5 4.0 3.2 4.123106    1.419716    -0.051777
5   NaN NaN NaN NaN         1.000000    -0.028557

図6.32 通常クリギングによる推定結果

z_ok = sum(df_simple_2['w'][0:5] * df_simple_2['z'][0:5])
s2_ok = df_simple_2['w'][len(df_simple_2) - 1] + sum(df_simple_2['w'][0:5] * df_simple_2['B'][0:5])
cv = np.sqrt(s2_ok) / z_ok
print(z_ok, s2_ok, cv)

4.828319580970582 0.03375263348265488 0.038050277103642186

関数例が誤っていると思われる。正しくは =INDEX('データ（3）'!\$D\$4:\$H\$8,B11,C11) ↩
=(J6-K6)^2 がK6セルと指定されているが、O6セルから上にコピー ↩

『クリギング入門』のPython実装

テキスト「6.2 Excelを用いた計算」のPythonでの実行

(1) バリオグラム推定

(2) 単純クリギング

(3) 通常クリギング