はじめに
スタンフォード大学 Andrew Ng氏による機械学習の講義動画を各週社内メンバーで持ち回りで受講し、学んだことを発表、Qiitaで共有しています。
その第三回が今回の記事です。
社内輪講をやるにあたっての記事です。
【機械学習】社内輪講はじめました
これまでの講義内容
【機械学習】社内輪講 Week1 〜 線形単回帰 〜
【機械学習】社内輪講 Week2 〜線形重回帰〜
ロジスティック回帰とは
これまでの講義の中では、家の価格を、一つもしくは複数のパラメータから推測するために、線形回帰(重回帰)を用いて行いました。
今回は、分類(良い・悪い、ある・なし)を推測する方法として、今までの講義で学んだ回帰を用いて行って行きます。
それをロジスティック回帰と言います。
仮定関数
具体例として下記の腫瘍の大きさで悪性かどうかを考えていきます。
今まで学んだ線形回帰の場合は、仮定関数$h_\theta(x)$は特に範囲指定はしておりませんでしたが、今回のような分類課題においては求めるものの特性上、仮定関数の取りうる値を$0≦h_\theta(x)≦1$と考えます。
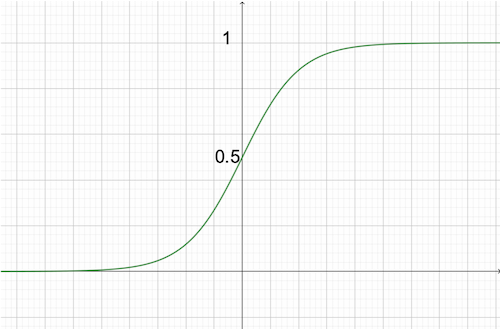
そこで登場するのがシグモイド関数$g(z)=\frac{1}{1+e^{-z}}$です。
この関数では、どのような値$z$を入れても$0≦g(z)≦1$になります。
また、前回の講義で導き出した重回帰の仮定関数$h_\theta(x) = \theta^Tx$をシグモイド関数に代入します。
h_\theta(x) = \frac{1}{1+e^{-\theta^Tx}}
こちらの関数が今回ロジスティック回帰における仮定関数となります。
- $h_\theta(x) ≧ 0.5$ の時 $y = 1$(悪性)
- $h_\theta(x) < 0.5$ の時 $y = 0$(良性)
さて、ここで、この仮定と実際のデータとの差を最小にする$θ$を探すために
目的関数(損失関数)を導入します。
目的関数(損失関数)
ロジスティック回帰においては、良性・悪性か、アウト・セーフなど0・1の分類を行います。
そのため、損失関数$Cost(h_\theta(x),y)$として、
- 仮定関数$h_\theta(x)$が実際のデータと一致していれば損失関数が最小値:0
- 仮定関数$h_\theta(x)$が実際のデータと一致してなければ損失関数が最大値:∞
をとるような損失関数$Cost(h_\theta(x),y)$を考えます。
そこで登場するのが$log$です。
数学が苦手な人は$log$を意識しなくても大丈夫です。
ここで大切なことは、今回の場合、$log$は0または∞を考慮する上でもっとも適しているからです。
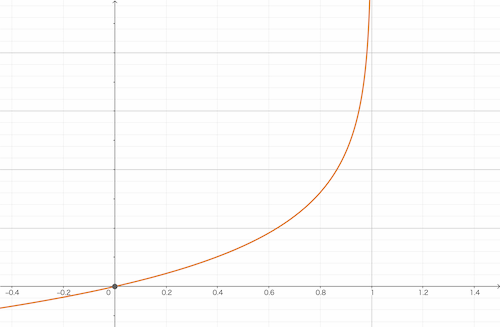
まず、$y = 1$の時
Cost(h_\theta(x),y) = -log(h_\theta(x))
とすると下のようなグラフになります。
グラフを見ると、
- $y=1$の時は$Cost(h_\theta(x),y)$が0
- $y=0$の時は$Cost(h_\theta(x),y)$が∞
になることが確認できます。
では、逆に$y = 0$の時は
Cost(h_\theta(x),y) = -log(1-h_\theta(x))
とすると下のようなグラフになります。
グラフを見てみると、
- $y=0$の時は$Cost(h_\theta(x),y)$が∞
- $y=1$の時は$Cost(h_\theta(x),y)$が0
になることが確認できます。
上記2つの式をまとめると以下のようになります。
Cost(h_\theta(x),y) = -ylog(h_\theta(x))-(1-y)log(1-h_\theta(x))
ここで、線形回帰の時の目的関数$J(\theta)$を考えます。
J(\theta) = \frac{1}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2
$\sum$の中を先ほどの損失関数におきかえると下の式になります。
J(\theta) = -\frac{1}{m}\sum_{i=1}^{m}(y^{(i)}log(h_\theta(x^{(i)}))+(1-y^{(i)})log(1-h_\theta(x^{(i)})))
さて、今回のロジスティック回帰における目的関数$J(\theta)$が求められました。
この目的関数に置ける最小のパラメータ$\theta$を求めるために使用するのは、線形回帰の時と同じ最急降下法となります。
最急降下法
前回と同様に下記最急降下法について考えていきます。
\theta_j := \theta_j - \alpha\frac{\delta}{\delta\theta}J(\theta)
実は、ロジスティック回帰の場合も同じ式を用いて行います。
唯一違うのは$h_\theta(x)$がシグモイド関数であるという点です。
これで無事、ロジスティック回帰を求めることができました。
複数クラスの分類
これまでは良いか悪いかなど、2つのクラスを分類する方法を学んできましたが、世の中には2つのクラスだけでは分類しきれないものがたくさんあります。例えば、明日の天気は晴れなのか、曇りなのか、雪なのか。そんな時は、one vs allという方法を使います。
考え方は今まで学んだロジスティック回帰と変わりません。
上図で考えると、まず、三角vsその他で回帰モデルを作成、次に、四角vsその他で回帰モデルを作成、最後に丸vsその他で回帰モデルを作成と、モデルをクラスの数分作成します。
そして、それぞれの分類器に対し、入力$x$を入れて実行し、$maxh_\theta^{(i)}(x)$となるクラス$i$を導き出す、ということを行います。
つまり、二値で学んだことを使い、求めたいクラスの数だけ分類器を作成し、入力に対して、もっとも高い確率を示すクラスを導き出します。
この方法にてマルチクラスの分類を行います。
正則化
オーバーフィッティングとは?
これまでの講義において、仮定関数$h_\theta(x)$は直線(下図:左)にて表してましたが、直線だけでなく、曲線を用いて、よりデータにフィットさせる多項式回帰(下図:中心、右)があります。
左 : $h_\theta(x)=\theta_0+\theta_1x$
中心 : $h_\theta(x)=\theta_0+\theta_1x+\theta_2x^2$
右 : $h_\theta(x)=\theta_0+\theta_1x+\theta_2x^2+\theta_3x^3+\theta_4x^4\cdots$
図をみてわかるように多項式回帰を用いて$x$の次数を増やしていくと、トレーニングデータに対してどんどんフィットしていきます。
ですが、ここで問題になるのは、トレーニングデータ = 実データではないということです。
例えば、上図右では、トレーニングデータに対してはほぼ100%フィットしていますが、明らかに実データを使うと精度が悪そうです。
このように、特定のデータに特化しすぎて、実データには役に立たないことをオーバーフィッティングと言います。
逆に上図左のようにトレーニングデータにフィットしなさすぎることをアンダーフィッティングと言います。
ここでは、オーバーフィッティングを防ぐ正則化という方法を紹介します。
損失関数の正則化
正則化の基本的な考え方は、パラメータ$\theta$の値を小さくすれば、$x$の次数が増えても、仮定関数$h_\theta(x)$への影響をできるだけなくすということです。
まずは、正則化パラメータ$\lambda$を損失関数$J(\theta)$に加えます。
J(\theta) = \frac{1}{2m}[\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})^2+\lambda\sum_{j=1}^n\theta_j^2]
損失関数$J(\theta)$に正則化パラメータ$\lambda$を入れることにより、$\lambda$をコントロールすることで、パラメータ$\theta$を調整することができます。
最急降下法の正則化
では、正則化された損失関数を最急降下法に代入します。
\theta_j := \theta_j(1-\alpha\frac{\lambda}{m})-
\alpha\frac{1}{m}
\sum_{i=1}^m(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)}
正則化パラメータ$\lambda$を入れることで$\theta_j$のアップデートに関して影響を与えます。
基本的に$(1-\alpha\frac{\lambda}{m})<1$なので、アップデートする際に、$\theta_j$の値を小さい方向に影響を与えてきます。
残りの式は元の最急降下法と同様のものになります。
正則化パラメータ$\lambda$を加えた際の仮定関数$h_\theta(x)$のイメージは下図になります。
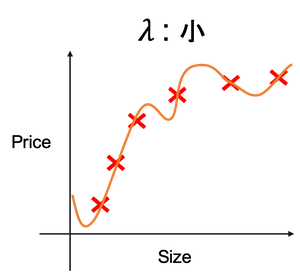
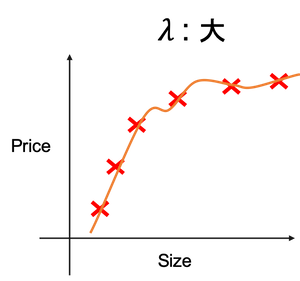
また、正則化パラメータ$\lambda$を扱う注意点としては、$\lambda$の値が大きすぎると、$\theta_0$以外の全ての$\theta$が限りなく0になり、
$h_\theta(x) = \theta_0$となります(下図)。
まとめ
- ロジスティック回帰は、線形回帰分析の数式を応用して求めることができる
- ロジスティック回帰と、線形回帰の違いは、仮定関数にシグモイド関数を使っている
- 複数クラスの分類はクラスの数だけ分類器を作ることで求められる
- 正則化を行うことで、オーバーフィッティングを防ぐことができる
次回は、いよいよニューラルネットワークに突入していきます!