評価
今回は、予測関数![]() の正確性、要するに精度を定量的に表す方法について。
の正確性、要するに精度を定量的に表す方法について。
未知データ![]() に対して、
に対して、![]() が出力する予測値ができるだけ正確であることが求められる。
が出力する予測値ができるだけ正確であることが求められる。
交差検証(クロスバリデーション)
<回帰問題の検証>
モデルの評価は、学習データをテスト用と学習用に分けて、テスト用のデータでモデルを評価する。例えば、学習データが10個あったとしたら、3:7など学習用の方を多めにして分ける。

学習済みのモデルがどれくらいテスト用データにもフィットしているかどうかを確認して評価していく。
ただし、図に書くことが難しい場合などが多いことから、定量的に精度を計算する必要がある。
回帰の場合は、学習済みのモデルに対してテスト用データで誤差の2乗を計算してその平均を取る。
テスト用データがn個あるとき、式は次のようになる。

これは平均二乗誤差(またはMSE(Mean Square Error))という値で、この誤差が小さければ小さいほど精度が高い良いモデルということになる。

交差検証の中でも、特にK分割交差検証という手法がある。
・学習データをK個に分割する。
・K-1個を学習用データ、残りの1個をテスト用データとして使う。
・学習用データとテスト用データを入れ替えながらK回の交差検証を繰り返す。
・最後にK個の精度の平均を計算して、それを最終的な精度とする。

ただし、学習データが多ければ、何回も学習する必要があるため時間がかかる。
適切なKを決めることが大切。
<分類問題の検証>
回帰の時と同じように、テスト用と学習用がそれぞれ次のように分かれている場合を考える。

次は、学習用データは完璧に分類できているが、テスト用データを完全に無視してしまっている例。

ロジスティック回帰では、分類が成功したかどうかは次の4種類の状態を考えることが大切。表にすると、

横長であることを正、横長でないことを負、とすると一般的に二値分類の結果は次のような表で表すことができる。

・Positive:分類結果が正
・Negative:分類結果が負
・True:分類がうまくできている
・False:分類が失敗している
分類の精度は、上記の表の4つの記号を使って計算できる。
TPとTNがどれだけあるかという割合が分類の精度(Accuracy)ということになる。

例えば、データが100個あって、そのうち、80個が正しく分類できたなら、精度は次のようになる。

適合率と再現率
次のようなデータの場合、全体の精度を見るだけでは不確か。
なぜなら、全部をNegativeだと分類しても、精度は95%となるため(NegativeがPositiveに比べ非常に多いため)。

Positiveがうまく分類できていない例。

1つ目の指標として、**適合率(Precision)**というものがある。

TPとFPにだけ注目する。この式は、Positiveと分類されたデータの中で実際にPositiveだったデータの数の割合ということ。

実際に代入して、

この適合率の値が高ければ高いほど、間違った分類が少ないということになる。今回の例では、Positiveに分類されたデータは3つあるが、実際にはそのうち1つしか正解ではないため、適合率は低い値となる。
また、**再現率(Recall)**とよばれる指標もある。この式は、Positiveデータの中で、実際にPositiveだと分類されたデータの数を表している。


実際に代入して

この値が高ければ高いほど、取りこぼしなく正しく分類しているということ。
今回の例だと、Positiveデータは全部で5個あるけど、実際には、そのうち1つしかPositiveには分類されていない。
よって、再現率も低い値になっている。
つまり、適合率と再現率の両方が高い値になっていれば、良いモデルだといえる。
ただし、適合率と再現率はどちらかが高くなればどちらかが下がるというトレードオフの関係にある。
F値
総合的な性能をはかるものとして**F値(Fmeasure)**という指標がある。
適合率か再現率かどちらかが低ければ、それに引っ張られてF値も低くなるようになっている。

次のような2つのモデルの例があるときを考えてみる。

また、TNをメインに適合率と再現率を考えることも可能で、そのときの式は次のようになる。

*データに偏りがあるときは数が少ない方を使うと良い。
正則化
学習データにしかフィットしないような状態を過学習(Overfitting)という。
(![]() の次数を増やしすぎると過学習になることからもわかる。)
の次数を増やしすぎると過学習になることからもわかる。)
<過学習への対応>
・学習データの数を増やす
・モデルを簡単なものに変更する
・正則化
回帰の目的関数:

これに、正則化項とよばれる次のような項を追加する。

実際に追加すると、

この新しい目的関数を最小化していくことを正則化という。
(注意)
・mはパラメータの個数
・![]() に対しては正則化は適用しないので、
に対しては正則化は適用しないので、![]() となっている。
となっている。
予測関数が のとき、
のとき、![]() となって、正則化の対象になるパラメータは
となって、正則化の対象になるパラメータは![]() と
と![]() ということになる。
ということになる。
![]() のようなパラメータだけの項はバイアス項といい、普通は正則化しない。
のようなパラメータだけの項はバイアス項といい、普通は正則化しない。
・λは正則化項の影響を決める正の定数。これはどういう値にするかを自分で決める必要がある。
以上のようにして、過学習を防ぐことができる。
この![]() と
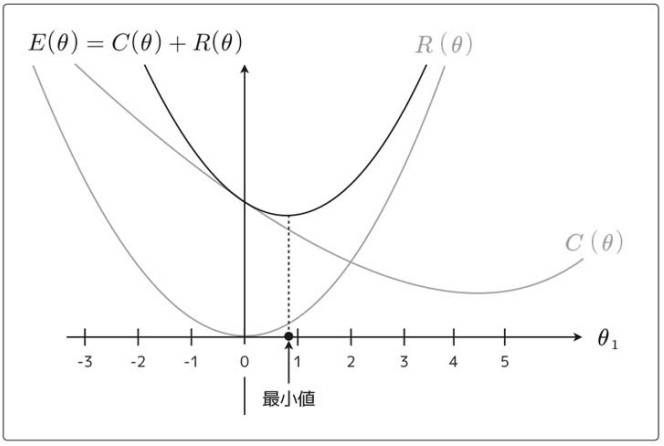
と![]() を足したものが新しい目的関数となるため、実際にこの2つの関数をグラフにプロットして足してみる。
を足したものが新しい目的関数となるため、実際にこの2つの関数をグラフにプロットして足してみる。
(ただし、パラメータの数が多いとグラフが書けないため、ここでは![]() だけに注目して考える。また、わかりやすくするためにλも省略する。)
だけに注目して考える。また、わかりやすくするためにλも省略する。)

実際の目的関数は、この2つを足した で、それは次のようなグラフとなる。
で、それは次のようなグラフとなる。
(![]() の各点で
の各点で![]() の高さと
の高さと![]() の高さを足して、それを線で結んでいく。最小値
の高さを足して、それを線で結んでいく。最小値![]() )
)
正則化項を足す前と比べて、![]() が0に近づいている。
が0に近づいている。
これが正則化項の効果で、パラメータが大きくなりすぎるのを防いで、小さい値に近づけてくれる。各![]() に対して、同様の動きをする。
に対して、同様の動きをする。
そしてパラメータの値が小さければ、それだけその変数の影響を小さくできるということで、次のような予測変数![]() を考える。
を考える。
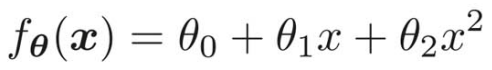
例えば、![]() のとき、
のとき、![]() は消え、2次式ではなくなり1次式となる。
は消え、2次式ではなくなり1次式となる。
つまり、もともとは曲線だった予測関数が直線になる。

不要なパラメータの影響を小さくすることで、複雑なモデルを単純なモデルに変えて過学習を防ぐ。
(ただし、最も次数の高い項のパラメータの値が小さくなるとは限らない。)
パラメータの影響が大きくなりすぎないように、ペナルティを課しながら学習していくという感じ。
またλは、その正則化のペナルティの度合いを調整する役割をしている。
<分類の正則化>
分類にも同じように正則化を適用できる。
ロジスティック回帰の目的関数、つまり対数尤度関数は、次のような式なので、

回帰の時と同様に、正則化項を足すと、

(注意)
元の目的関数にマイナスがついているのは、対数尤度関数は、元々は最大化することが目的だったが、今回は(誤差を最小化する)回帰の目的関数と合わせて最小化問題として考えたいため。
符号を反転させたので、パラメータの更新の時は回帰と同じように微分した関数の符号と逆方向に動かすようにすることに気をつける必要がある。
目的関数の形が変わったので、パラメータ更新式も変わり、次はそれについて考えていく。
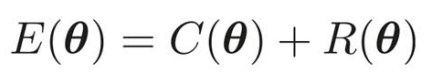 なので、
なので、

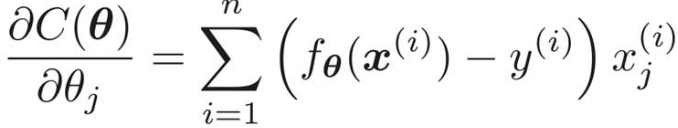
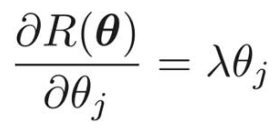
したがって、最終的な微分結果は次のようになる。

この微分結果をパラメータ更新式にあてはめると、

(注意)
![]() に関しては正則化は適用しないので、
に関しては正則化は適用しないので、![]() を
を![]() で微分すると0になるため、場合分けする必要がある。
で微分すると0になるため、場合分けする必要がある。
ロジスティック回帰も同じような流れで、微分していくと、
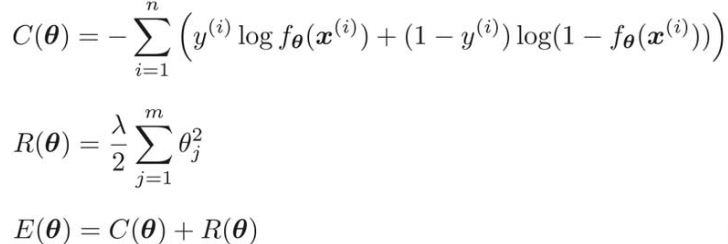
ロジスティック回帰の元の目的関数![]() の微分は、以前求めたものにマイナスををつけているところに注意(今回は最小化問題として考えているため。)
の微分は、以前求めたものにマイナスををつけているところに注意(今回は最小化問題として考えているため。)


したがって、パラメータ更新式は、回帰同様、場合分けをして、次のようになる。

学習曲線
過学習とは逆で、学習データにフィットしていない状態のことを**未学習(Underfitting)**という。
例えば、次のようなグラフで複雑な境界線を持つようなデータを直線で分類しようとすると、どうやっても綺麗に分類できずに結果的に精度が悪くなる。
この原因は、解きたい問題に対してモデルが単純すぎるという点にある。
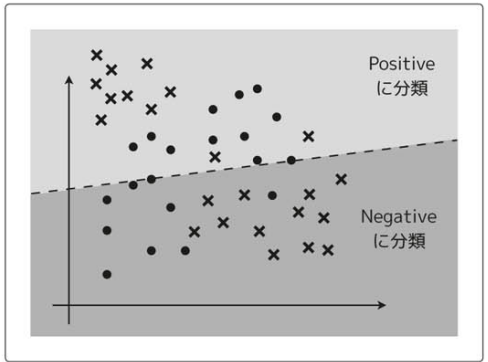
過学習か未学習かを見極めるには学習曲線を使う。
精度だけでは、どちらが原因かわからないため、横軸をデータの個数、縦軸を精度として、学習用データとテスト用データの精度をプロットしてみる。

ここでは、![]() を1次関数として話を進めることにする。この中から適当に学習用データを2個だけ選んで、それで学習を進める。
を1次関数として話を進めることにする。この中から適当に学習用データを2個だけ選んで、それで学習を進める。
 このグラフだと学習用データ2個についてはどちらにもフィットして誤差は0。
このグラフだと学習用データ2個についてはどちらにもフィットして誤差は0。
次は、学習用データ10個で学習してみる。誤差を0にするには、あまりに難しすぎるのがわかる。

つまり、モデルが簡単すぎる場合はデータ量が増えるにつれて、誤差も少しずつ大きくなり、精度が下がっていく。
横軸をデータの個数、縦軸を精度とするグラフを書いてみると、次のように、最初は精度が高いが、データ量が増えるにつれて精度が少しずつ下がるようになる。

先ほどの学習用データ10個とは別にテスト用データがあるとして、それぞれのモデルでテスト用データの評価をして、同じように精度を求めてプロットしてみる。
学習用データが少ない時のモデルでは、未知のデータを予測することは難しいから精度が低くなる。
一方で、学習用データが多くなればなるほど、少しずつ予測の精度が上がっていく。

<未学習の状態(**ハイバイアス**)のグラフ>
データの個数を増やしたとしても、学習用データでもテスト用データでも精度が悪い状態のグラフになる。

<過学習の状態(ハイバリアンス)のグラフ>
学習用データに対してはデータを増やしてもずっと精度が高いままで、テスト用データに対しては精度が上がりきれていない状態のグラフになる。学習用データにだけフィットしいてしまうという過学習の特徴が見て取れる。
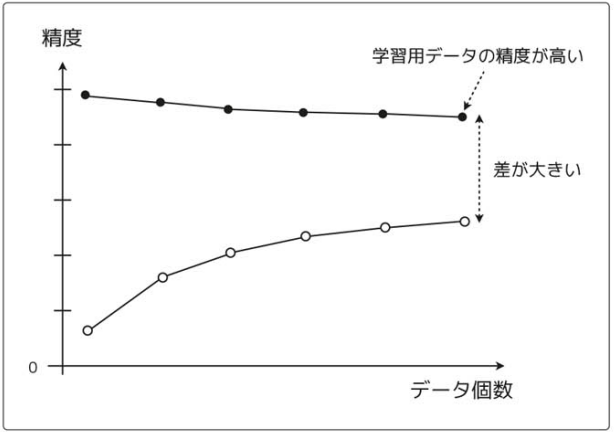
モデルの精度が悪い時に、過学習か未学習かわからないときは、学習曲線を描くといい。








