機械学習勉強会での Julia の発表と参加者の反応レポート

Last updated at 2015-12-04Posted at 2015-12-02

初めに

2015/11/28 に、機械学習名古屋第2回勉強会という勉強会を開催してきました¹。

メインは「K-means 実装ハンズオン」（Python + numpy 利用）だった¹のですが、そのあとの発表で Julia についてプレゼンをしてきたので、その概要と、反応をレポートします。

発表資料

発表資料は Jupyter で作成し、nbconvert でスライドに変換して Github Pages で公開²³。

URL: http://antimon2.github.io/MLNGY_201511/slides/AboutJulia.slides.html

構成

Julia とは？
機械学習への適用〜自分で実装編〜
- 例1：単純な線形回帰
- 例2：簡単な K-means
機械学習への適用〜追加パッケージ利用編〜
- 機械学習ライブラリ（主なもの）
- 例1：Regression.jl で線形回帰
- 例2：Clustering.jl で K-means

発表概要

機械学習勉強会での発表ではありますが、今回はあくまで Julia の紹介レベル。
簡単な学習ならシンプルに実装出来ますよ、あと有志が便利な機械学習系のパッケージを公開しているので利用することもできますよ、程度の内容です⁴。
ただ、簡単な実装例を示すことで、ついでに Julia のコード例の紹介も行いました。

次節で、発表資料中の実装例1・2をこの記事用に再編・再掲し、ついでに Julia のコード解説もしなおしてみます。

コード例の紹介（および補足）

また以下のポイント解説中で、特に断りのない箇所は実際に話した内容、「《補足》」はこの記事を書くにあたって付加した補足説明、「【反応】」とある箇所は参加者から質問・意見等の反応の記録です。

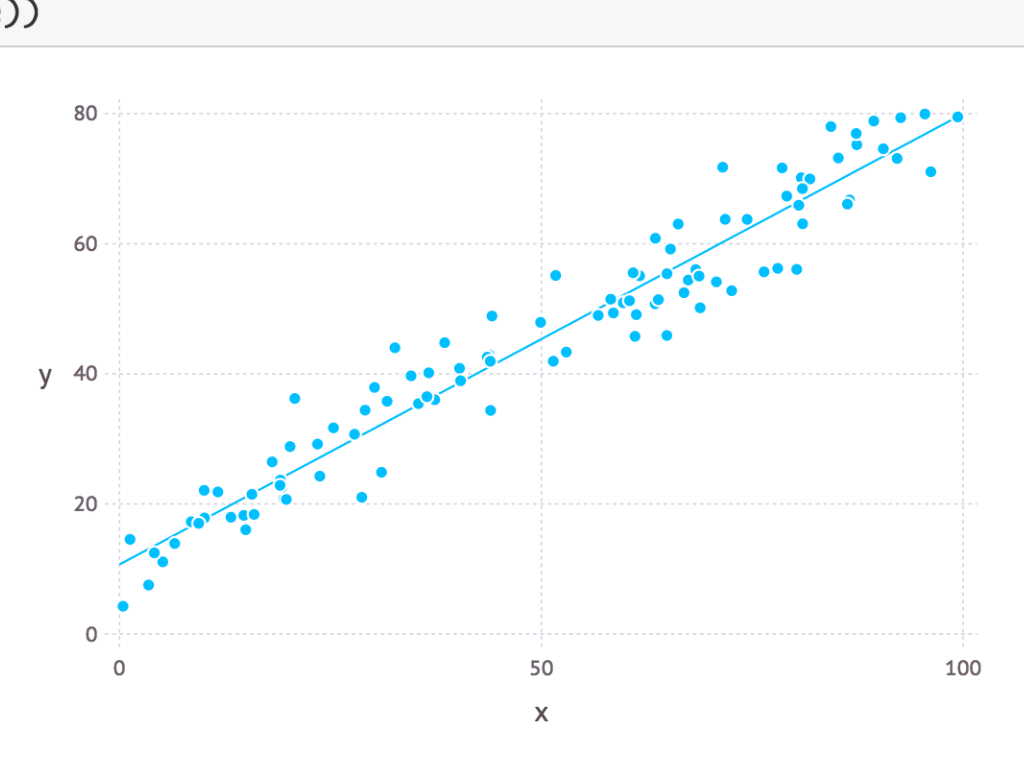
例1：単純な線形回帰

Julia v0.4.x/v0.3.x どちらでも動作します（次の例も同様）。

linreg1.jl

# 手作りサンプルデータ
x = rand(100) .* 100
y = randn(100) .* 5 .+ x .* 0.7 .+ 10

# 行列作成
X = [ones(100, 1) x;]

# パラメータ求解（Normal Equation 利用）
# θ = X \ y
θ = (X' * X) \ (X' * y);

# 結果プロット
using Gadfly  # ← Julia 定番のデータプロットライブラリ

x_linspace = linspace(0,100)
f(x) = θ[1] .+ x .* θ[2]
plot(layer(x=x, y=y, Geom.point), layer(x=x_linspace, y=f(x_linspace), Geom.line))

プロット例：

（※plot は Julia Console や Jupyter 上等でないと表示されないかもしれません。以下同）

ポイント解説：

2,3,6,10,16行目：ベクトル・行列の書式や演算の多くは、MATLAB/Octave 由来。
.*, .+ 等は「要素ごとの演算」で、相手がスカラーなら「全要素に対する演算」となる。
10行目：θ を変数名として使用。Julia では unicode 文字列も識別子として扱える。
- 【反応】Q：unicode 文字列を利用して新しい演算子とか定義出来ない？
  → A：ある程度可能。標準では例えば、≤,≥ 等の不等号演算子が存在する。ちなみに演算子も関数。
- 【反応】Q：2引数関数を中置演算しとして利用（Haskellの `div`のような書き方）は可能？
  → A：不可能。一部の記号文字からなる関数が演算子として利用出来るだけ。
10行目：X が縦長（＝行数が列数より多い）行列の場合、バックスラッシュ演算子による演算 X \ y はこのように (X' * X) \ (X' * y) と書ける。この方が速い⁵。
- 《補足》Julia 標準で用意されている関数を用いて linreg(x, y) と書くことで同じ結果が得られるが、内部実装は上述の X \ y 相当になっています。
- 《補足》あと、最近気付いたのですが、この書き方の場合は * を省略出来て X'X \ X'y とも書ける。
16行目：この f(x) = 〜 のように、インラインで関数定義もできる。
- 《補足・訂正》この書き方も MATLAB/Octave 由来と思っていた（その時そう説明した）のですが、なんか違ってたみたいです。詳細判明したらさらに追記するかもです。
- 《補足》あとここも先ほどと同様、*を省略出来て f(x) = θ[1] + θ[2]x とも書けます。

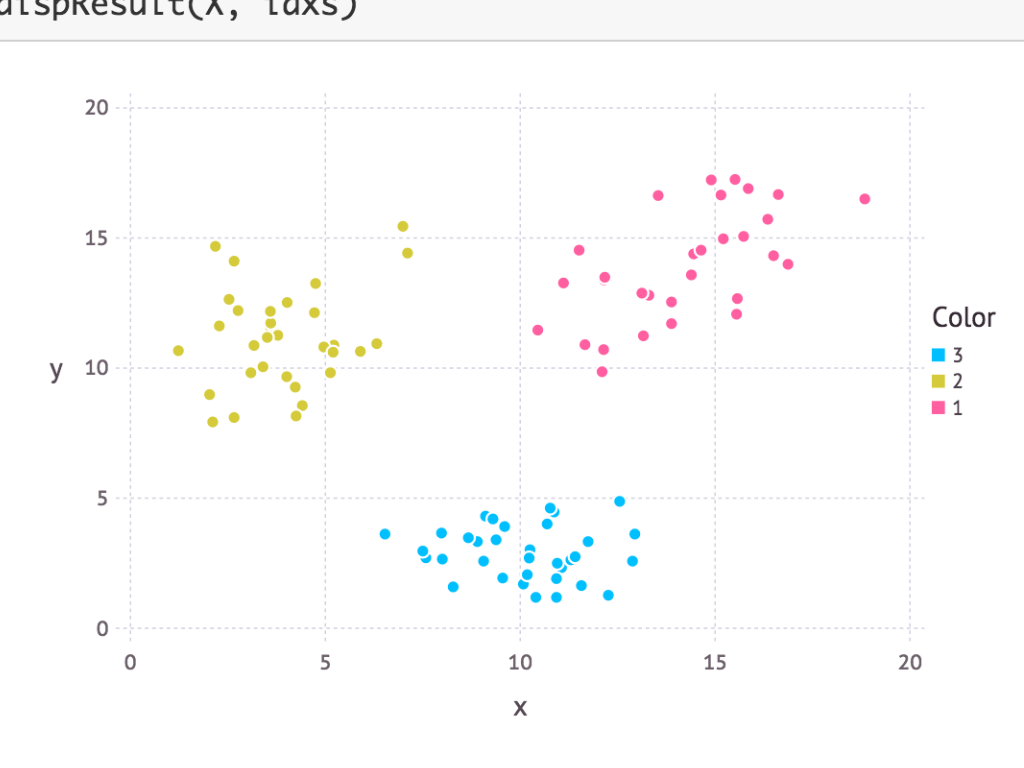
例2：簡単な K-means

当日のハンズオンで使用したデータ（過去に CodeIQ で出題された問題のサンプルデータ）を利用。

kmeans1.jl

using Gadfly

# データ読込
data = open(readdlm, "./CodeIQ_data.txt", "r")

K = 3
X = data;

# クラスタ重心初期化
function initCentroids(X, K)
    randidx = randperm(size(X, 1))
    X[randidx[1:K], :]
end

# クラスタ割り付けステップ
function findClosestCentroids(X, centroids)
    K = size(centroids, 1)
    map(1:size(X, 1)) do i
        x = vec(X[i, :])
        ts = [x - vec(centroids[j,:]) for j=1:K]
        ls = [dot(t, t) for t=ts]
        indmin(ls)
    end
end

# 重心移動ステップ
function computeCentroids(X, idxs, K)
    m, n = size(X)  # m 不使用
    centroids = zeros(K, n)
    for j = 1:K
        centroids[j, :] = mean(X[idxs .== j, :], 1) # ← idxs が j（=1,2,…,K）の行のみ抽出して、列ごとに平均値を算出
    end
    centroids
end

# ループ実施
function runKMeans(X, initialCentroids, max_iters=10)
    m, n = size(X)
    K = size(initialCentroids, 1)
    centroids = initialCentroids
    prev_centroids = centroids
    idxs = zeros(m, 1)
    
    for i = 1:max_iters
        idxs = findClosestCentroids(X, centroids)
        centroids = computeCentroids(X, idxs, K)
        if centroids == prev_centroids
            break
        end
        prev_centroids = centroids
    end
    
    return centroids, idxs
end

# 結果表示
function dispResult(X, idxs)
    plotdata = [X [string(i) for i=idxs];]
    plot(x=plotdata[:,1], y=plotdata[:,2], color=plotdata[:,3])
end

# 実行
initial_centroids = initCentroids(X, K)
centroids, idxs = runKMeans(X, initial_centroids)
dispResult(X, idxs)

プロット例：

ポイント解説：

4行目：ファイルの読み込み。readdlm() 関数は「各行ごとにホワイトスペースを区切子として分割して適切な型に変換した結果からなる行列を返す」という動き。タブ区切りファイルを読み込むときなどの定石的な書き方。
- CSVファイル（","区切り）を読み込む場合はreadcsv()関数が利用出来る。
6行目：K = 3（クラスタ数）は目視で確認。
- 【反応】Q：目視ではなく、それもプログラム側に任せる方法はないのか？
  → A：ある。ノンパラメトリックベイズモデル⁶とか。K を少しずつ変化させて学習曲線引いて K-means を何度か試し、最適化時のコストが「それ以上Kを増やしてもあまり変わらない」時のKを選択するとか（coursera のオンライン機械学習コースではこの方法を紹介している）。
9〜54行目：ベクトル・行列の処理で色々テクニックを使用しているが、時間の都合で詳細説明略。
- 《補足》この記事を借りて少しだけ説明：
- vec(A)（A：配列）は、Xをベクトル（1次元の配列）に変換する。A[:]と書いても同じ結果が得られる（がvec()の方が圧倒的に速い）。
- dot(x, y) は、ベクトルのドット積（内積）。
  Julia の場合 x' * y と書くと 1要素のベクトルになってしまうので (x' * y)[1] と明示的に添え字指定して値を取り出さねばならない上に、dot(x, y) の方が圧倒的にパフォーマンスが良い。
- [v for v=〜]は、Julia のリスト内包表記。書き方は Python のそれに類似（ただし条件節は記述出来ない）。
- size(X)（X：行列（＝2次元配列））は、Xの行数と列数からなる tuple を返す。
- size(X, d)（X：2次元以上の配列）は、Xの指定された軸の数（dが1なら行数、2なら列数、…）を返す。
【反応】Q：for文が目立つけれど、Julia は LLVM の JIT コンパイルが走るから、下手にベクタライズするよりfor文使った方が速くなる？
→ A：その通り。よくご存じで⁷。
- 《補足》例えばこちらを参照 → Juliaではfor文を使え。ベクトル化してはいけない。 - りんごがでている
  今回も実際、いくつかの書き方で試して割とパフォーマンスが良いモノを選んでみたら、for文が割と多くなり、下手にベクタライズしての処理が少なく（付言すると標準の関数として用意されているものをなるべく利用するカタチに）なりました（上述の vec() dot() 等）。

総括、その他

思いの外、参加者の食いつきが良かった、という印象です。

何より、ベンチマークや言語仕様を見て「使えそう」「選択肢が増えた」「○○を Python でやろうと思ってたけれど Julia でやってみようかな」といったリアクションがありました！
嬉しいですね。紹介した甲斐があったってもんです。
これで Julia 人口が少し増えるかな、と期待。

主催者の1人（Hero Miwa 氏と共催）です。なおハンズオンでは講師役やりました。 ↩ ↩²
ちなみにハンズオン用の資料も同じ方法で作成・公開。→ http://antimon2.github.io/MLNGY_201511/slides/K-means.slides.html ↩
以前 Jupyter でスライド作成したときは nbviewer で公開していたのですが、最近こちらのスライド表示機能がおかしい（1ページに収まってしまってページ遷移出来ない）ので、自前でスライドに変換するようにしました。今後もこの方法の方がよっぽど良いかも。 ↩
もっと高度な内容とか「Tens○rFl○w 動かしてみた」とか期待していた方、期待に添えずスミマセン。 ↩
拙過去記事線形回帰の Normal Equation（正規方程式）について参照。 ↩
私の後に別の方がその発表をしたのですが、資料等は公開されていないようです。 ↩
正直、こんな高度な反応が上がってくるとは予想外でした。質問者はプロコンか何かの経験者らしいのでそういう知識があったのかもしれません。 ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up