この記事はAtCoder公式が出しているレート計算式の説明PDFの内容を解説しようと試みるものである。
AtCoder公式によるレート計算式の説明はPDF3ページに収まる非常に簡潔なものなのだが、その分背景知識や式の設計意図が大幅に省略されていて、原文を読むだけでは理解に悩む箇所も少なくない。
そこで、省略されている箇所をAtCoder公式の発言や私の予想で補って、できるだけわかりやすく解説しようとするのがこの記事の目的である。
この記事の目的上、この記事はAtCoder公式による説明を正確に理解するには全く向いていない。
私の予想が混じっているからである。
私の予想の部分はできる限りそうだと明示するようにするが、信頼できるソースを求めるのであれば原文を読むようにしてほしい。
また、私の数学力が足りていないために、式の設計意図を私が勝手に予想することすらできなかった箇所もある。
その部分は式の形だけ説明する。
レートとパフォーマンス
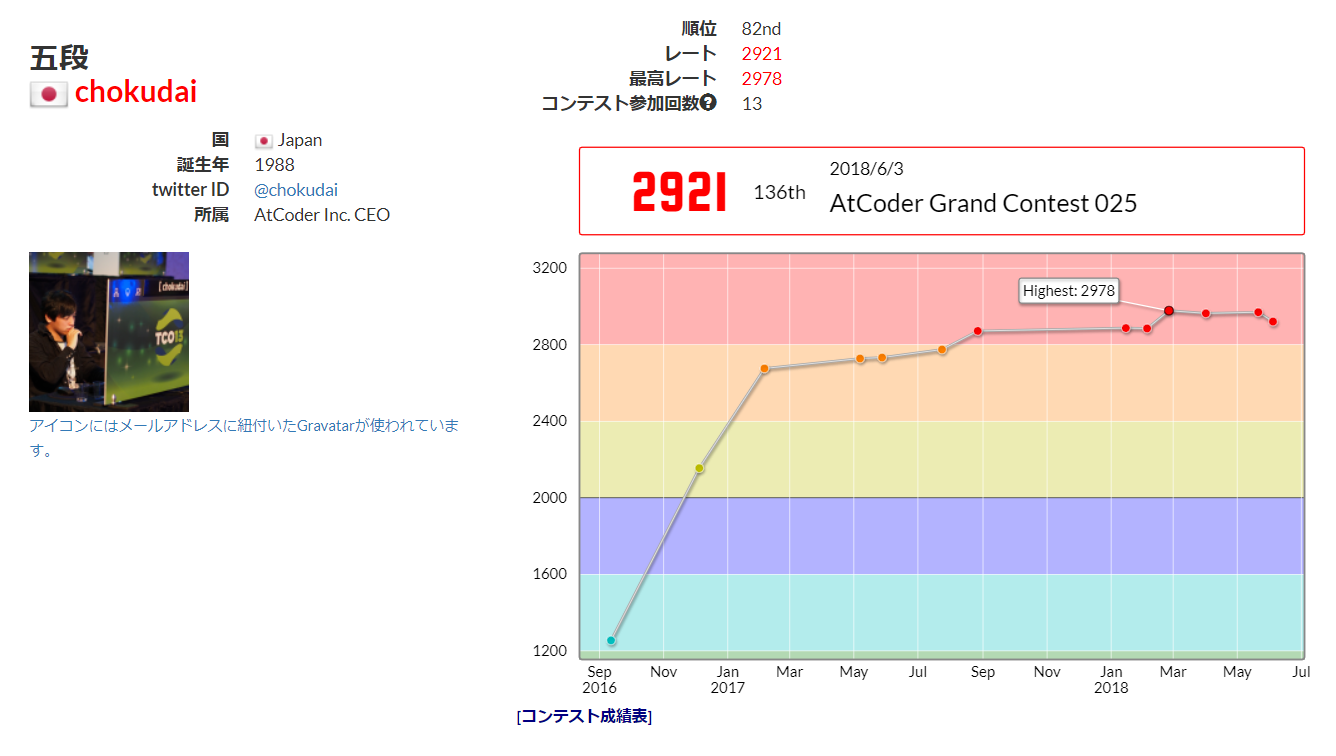
ユーザーの個人ページ(例: chokudai)に大きく掲載されている0以上の整数をレートと呼ぶ。
高ければ高いほどそのユーザーの競技プログラミングにおける実力が高いことを示す。
(私は理解できていないのだが、より厳密には、99.9%の確率でそのレート以上の実力があることを保証する数字、つまり99.9%上側信頼区間の下側信頼限界であるらしい)
ここでは**chokudai**のレートは2921であることが分かる。
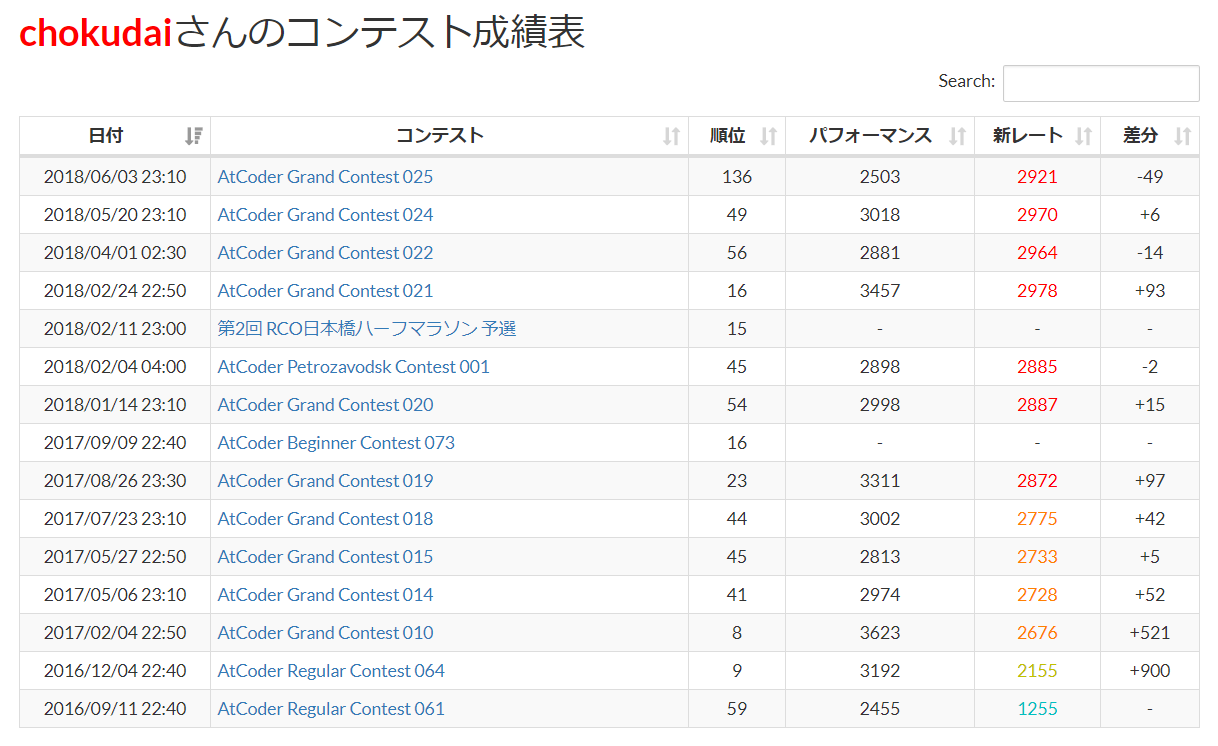
ユーザーの個人ページにある「コンテスト成績表」のリンクから飛べる画面で確認できる整数をパフォーマンスと呼ぶ。
パフォーマンスはあるユーザーのあるコンテストにおける成績を表し、高ければ高いほど良い。
パフォーマンスはレートと違って負の整数になることもある。
(2019/7/22追記)
……のだったが、2019年7月20日頃、パフォーマンスは表示上0以上の整数しかとらないように変更された。
この記事の内容はまだこの変更に追従できていない。
(追記終わり)
ここでは**chokudai**の各コンテストにおけるパフォーマンスは、新しい側から順に2503, 3018, 2881, ……であることが分かる。
あるユーザーのレートはそのユーザーのパフォーマンスのみから算出される。
RatedとUnrated
あるユーザーがコンテストに参加したとしても、以下のいずれかの場合はパフォーマンスが算出されずに「-」という表示になる。
または、そもそもコンテスト成績表に載らなかったりする。
- AtCoderのサイトを借りて行われる非公式コンテストや企業コンテストに参加した場合(ただし一部の企業コンテストは例外的にパフォーマンスが算出されることもある)
- 現在のレートと比べて簡単すぎるコンテストに参加した場合(基準は後述)
- 一回も回答を提出せずにコンテストを終了した場合
- AtCoder社のコンテスト運営に不備があり公平なコンテストを実施できなかった場合
このような、パフォーマンスが算出されないコンテストは、そのユーザーにとってUnratedなコンテストと呼ばれる。
例えば**chokudai**にとっては、少なくとも以下のコンテストがUnratedなコンテストである。
- 第2回 RCO日本橋ハーフマラソン 予選
- AtCoder Beginner Contest 073
レートはパフォーマンスのみから算出されるので、つまりUnratedなコンテストに参加した場合レートは変動しない。
逆にパフォーマンスが算出されレートが変動するコンテストはRatedなコンテストと呼ばれる。
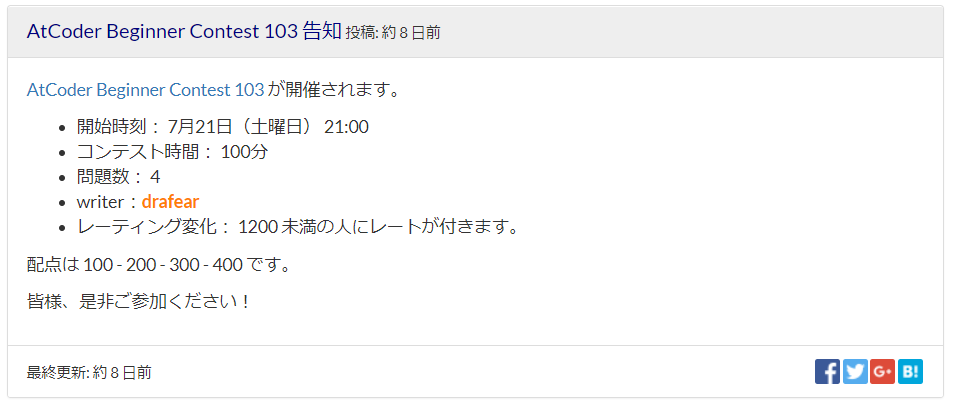
自分にとって次のコンテストがRatedになりうるか否かは、コンテストごとに決まっているRated対象を見ればそれだけでわかる。
この場合、このコンテストのRated対象は0〜1199であるから、自分の現在のレートが1199以下であり、かつ無提出でなく、かつAtCoder社のコンテスト運営に不備がなければ、このコンテストはRatedである。
逆に、自分の現在のレートが1200以上である場合、このコンテストは自分にとって簡単すぎるコンテストであるということになり、このコンテストはUnratedである。
特定の名前のコンテストはRated対象が毎回固定で決まっていて、以下の表のようになっている。
| コンテスト名 | Rated対象 |
|---|---|
| AtCoder Beginner Contest 042〜125 | 0〜1199 |
| AtCoder Beginner Contest 126〜 | 0〜1999 |
| AtCoder Regular Contest 058〜 | 0〜2799 |
| AtCoder Grand Contest 001〜 | 0〜∞ |
その他の名前のコンテストについては、Rated対象は毎回まちまちである。
ちなみに、AtCoder Beginner Contest 041以前とAtCoder Regular Contest 057以前は現在のレーティングシステムが始まる前のコンテストなので、上の表には載せていない。
無提出がUnratedになる理由は、おそらくは参加登録だけしたもののなんらかの事情で参加できなかったユーザーに対する救済措置である。
しかしながら、レートの減少を防ぐために苦手そうな問題ばかりだったらわざと回答しないようにする戦術(俗にNoSub撤退と呼ぶ)も有効になってしまうことには批判があり、将来的には問題を見た時点でRatedにするかもしれないとされている。(ソース1、ソース2)
処理負荷との兼ね合いもあるため、2018年7月30日現在ではNoSub撤退はUnratedである。
あるユーザーがRatedなコンテストに参加したとき、そのユーザーはそのコンテストにとってRatedな参加者であると呼ぶ。
また、あるユーザーがUnratedなコンテストに参加したとき、そのユーザーはそのコンテストにとってUnratedな参加者であると呼ぶ。
AtCoderのレーティングシステムの概要
AtCoderのレーティングシステムはイロレーティングをベースにしているものの、多数の改造が加わっているためもはや原型はほとんどない。
たとえばイロレーティングでは、レート差200のプレイヤー同士が対戦したときレートの高い方が約76%$\left(= \frac{1}{1 + 10^{-\frac{200}{400}}}\right)$の確率で勝利するはずである。
しかしAtCoderでは、レート差200のプレイヤー同士が同じコンテストに出場したときレートの高い方が何%の確率で高い順位になるというようなことは言えない。1
イロレーティングが持っていたレートの性質が失われているのは、おそらくは、イロレーティングをそのまま使用した場合に起きうる多数の問題に、AtCoderのレーティングシステムが対処しようとした結果だろう。
AtCoderの現在のレーティングシステムからその設計意図を逆算すると、どうやらAtCoderのレーティングシステムは以下のような性質を持つように設計されているようであり、そして実際そのような性質を持っている。
- (多分ユーザーのモチベーションのために)大成功を相対的に高い重要度で評価し、大失敗を相対的に低い重要度で評価する
- 新しいコンテストの結果を相対的に高い重要度で評価し、古いコンテストの結果を相対的に低い重要度で評価する
- あるユーザーが初参加のコンテストで失敗した場合、最初のコンテスト結果に引きずられてレートが伸び悩むのを防ぐためにアカウントを作り直そうとそのユーザーが考えることがない
- (多分初心者のモチベーションのために)初心者のレートが例えばマイナスのような低すぎる値になってしまうことがない
実際、あるユーザーのレートの計算手順は以下のようになっているので、上記性質をすべて満たす。
- 性質1, 2を満たすような特殊な平均を用いて、そのユーザーの全てのパフォーマンスをいい感じの一つの値に集計する。
- 手順1で求めた数字から、Ratedなコンテストへの参加回数に応じた補正値を減算する。この補正値は参加回数が1回しかなければ1200、2回しかなければ約745.4、……であり、参加回数が増えるにしたがって0に近づいていく。これにより高いレートを得るにはどのみち10回程度以上のコンテスト参加が必要になり性質3を満たすことができる。
- 手順2で求めた数字が400以下であれば(もちろん負の数であることもある)上方補正をかけることで0以上400以下の数字になるようにする。例えば400は400に、0は約147.2に、-400は約54.1に、……そして-∞は0になるようにする。これにより性質4を満たすことができる。
手順3で求めた数字を四捨五入2した値がレートとなる。
パフォーマンスの計算手順
AtCoderのレーティングシステムには、いわば内部パフォーマンスと呼ぶべき値3と、内部レートと呼ぶべき値4がある。
内部パフォーマンスとは
内部パフォーマンスは、コンテストごとに定められたパフォーマンス上限を考慮しない純粋なパフォーマンスである。
例えばAtCoder Beginner Contest 126〜においては、内部パフォーマンス2400以上の成績を収めても、パフォーマンス上限が2400であるために実際のパフォーマンスは2400に抑えられる。
\begin{align*}
\text{パフォーマンス} =& \min\left(\text{内部パフォーマンス}, \text{パフォーマンス上限}\right)\\
\text{パフォーマンス上限} =& \text{Rated対象の上限} + 401\\
\end{align*}
| コンテスト名 | パフォーマンス上限 |
|---|---|
| AtCoder Beginner Contest 042〜125 | 1600 |
| AtCoder Beginner Contest 126〜 | 2400 |
| AtCoder Regular Contest 058〜 | 3200 |
| AtCoder Grand Contest 001〜 | ∞ |
| その他 | まちまち |
なぜパフォーマンスに上限が存在するのかというと、おそらくは簡単なコンテストで良い結果を残す、つまり簡単な問題の早解きをするだけで高いレートを得られないようにするためだろう。
内部パフォーマンスは基本的には公開されていないのだが、実は内部のAPIを覗くと確認することが可能である。
例えば**anqooqie**の各コンテストにおける内部パフォーマンスは https://atcoder.jp/users/anqooqie/history/json のInnerPerformanceプロパティの値である。
{"IsRated":true,"Place":32,"OldRating":1025,"NewRating":1130,"Performance":1600,"InnerPerformance":1765,"ContestScreenName":"abc108.contest.atcoder.jp","ContestName":"AtCoder Beginner Contest 108","EndTime":"2018-09-01T22:40:00+09:00"}
これを見るに、内部パフォーマンスはパフォーマンスと同じく整数の値をとると考えてよいようである。
内部レートとは
内部レートはレートと同じくあるユーザーの実力を表す数値であるが、レートが持っている4つの性質のうち性質2(新しいコンテストの結果を重視)しか満たさない。
おそらくはこれが内部レートが内部レートである所以であり、外部にそのまま公開するには有害な情報だが数学的な扱いはその分容易となるだろう。
内部レートは内部パフォーマンスの重みつき平均であり、レートと違って実数として扱われているようである。5
\begin{align*}
\text{内部レート} =& \frac{\sum_{i=1}^\text{Ratedなコンテストへの参加回数} \text{新しい方から}i\text{番目の内部パフォーマンス} \times 0.9^i}{\sum_{i=1}^\text{Ratedなコンテストへの参加回数} 0.9^i}
\end{align*}
例えばあるユーザーが初参加のコンテストで内部パフォーマンス800をとったとき、そのユーザーの内部レートは800である。
\begin{align*}
\frac{800 \times 0.9}{0.9} &= 800
\end{align*}
同じユーザーが次のコンテストで内部パフォーマンス1600をとったとき、そのユーザーの内部レートは1600と800を$0.9:0.9^2$で重みつき平均した1221.0526315789473…である。
\begin{align*}
\frac{1600 \times 0.9 + 800 \times 0.9^2}{0.9 + 0.9^2} &= 1221.0526315789473 \ldots
\end{align*}
同じユーザーが次のコンテストで内部パフォーマンス2400をとったとき、そのユーザーの内部レートは2400と1600と800を$0.9:0.9^2:0.9^3$で重みつき平均した1656.0885608856088…である。
\begin{align*}
\frac{2400 \times 0.9 + 1600 \times 0.9^2 + 800 \times 0.9^3}{0.9 + 0.9^2 + 0.9^3} &= 1656.0885608856088\ldots
\end{align*}
内部パフォーマンスの算出
あるユーザーが新しいRatedなコンテストに参加して何位かでコンテストを終えたとき、そのコンテストにおける内部パフォーマンスがどのようにして算出されるか説明する。
あるユーザーの内部パフォーマンスの算出に用いられる要素は以下で全てである。
- Ratedな参加者だけで数えた場合のそのユーザーの順位(ただし順位の数え方はFractional Ranking、つまり同率順位は平均をとる)
- Ratedな参加者全員の、コンテスト参加前時点での内部レート(ただしRatedなコンテストに参加したことがないユーザーは内部レートが定義できないので、そのようなユーザーは以下のデフォルト内部レート6を内部レートとして扱う)
| コンテスト名 | デフォルト内部レート |
|---|---|
| AtCoder Beginner Contest 042〜 | 800 |
| AtCoder Regular Contest 058〜103 | 16007 |
| AtCoder Regular Contest 104〜 | 1000 |
| AtCoder Grand Contest 001〜033 | 16007 |
| AtCoder Grand Contest 034〜 | 1200 |
| その他 | (原文では明示されていない) |
強い人ばかり集まっている中で高い順位をとると内部パフォーマンスは非常に高い数字になる。
一方、初心者ばかり集まっている中で高い順位をとっても内部パフォーマンスはさほどでもない。
ユーザーuの内部パフォーマンスは以下の式を満たす唯一の実数xを四捨五入8した値である。
\begin{align*}
\sum_{r \in \text{全てのRatedな参加者}} \hspace{2em} \frac{1}{1 + 6^\frac{x - r\text{の内部レート} \hspace{1em}}{400}} &= u\text{のRatedな参加者内での順位} - 0.5\\
\end{align*}
一見どうやって解を求めればいいかわからなさそうだが、
\begin{align*}
f(x) =& \sum_{r \in \text{全てのRatedな参加者}} \hspace{2em} \frac{1}{1 + 6^\frac{x - r\text{の内部レート} \hspace{1em}}{400}}
\end{align*}
は狭義単調減少する関数なので二分探索で解を求めることができる。
内部パフォーマンス算出式の意味
前述の内部パフォーマンス算出式は、これを眺めるだけではその式の設計意図が何もわからない。
結局この式は定性的には何を求めようとしているのだろうか?
ところが原文は何も説明していない。
よってこの節は丸々すべて私の予想である。
私が予想するに、実はこれは、仮に自分と全く同じ順位をとった、別の内部レートが未知の参加者がいたとして、その参加者の最も尤もらしい内部レートの値を求めるものなのである。
今内部レートがそれぞれ1500, 1600, 1700, 1800の4名のRatedな参加者、A、B、C、Dがコンテストに参加したとしよう。
このうち参加者Cがあなたであるとする。
コンテストの結果は以下であった。
| 順位 | 参加者名 | 内部レート |
|---|---|---|
| 1 | D | 1800 |
| 2 | A | 1500 |
| 3 | C | 1700 |
| 4 | B | 1600 |
ここに、内部レートが未知の参加者Eが参戦したとしよう。
| 順位 | 参加者名 | 内部レート |
|---|---|---|
| 1 | D | 1800 |
| 2 | A | 1500 |
| 3 | C | 1700 |
| 3 | E | ? |
| 5 | B | 1600 |
Eは内部レート1800の相手と内部レート1500の相手に負け、内部レート1700の相手に引き分け、そして内部レート1600の相手に勝ったわけであるが、このときEの内部レートとして最も尤もらしい値は何だろうか?
実はそれがCの内部パフォーマンスである。
さて、当然何の仮定もなしではEの内部レートの値などわかるわけがないのだが、実はいくつかの仮定をおくことで、Eの内部レートの最も尤もらしい値を求めることが可能である。
以下の仮定をおくことにしよう。
- 参加者Eがある参加者Xに勝てる(Xより高い順位になれる)確率と、別のある参加者Yに勝てる確率は独立である
- 参加者Eがある参加者Xに勝てるかどうかはただ一つの要因、内部レートにより確率的に決定する。
- これら二つの仮定は、得意分野や問題傾向の概念を単純化のため意図的に考えないことを意味する。
- 参加者Eと内部レート差が同一である参加者X, Yがいたとして、EがXに勝てる確率とEがYに勝てる確率は同一である。
- この仮定は、すべての参加者において調子の崩しやすさは同一であると単純化のために考えることを意味する。
- 内部レート差が十分に大きいとき、内部レートの低い側が内部レートの高い側に偶然に勝てることはありえない。
- この仮定は、4択問題のような誰でも偶然に解ける問題が出題されないと考えることを意味する。
このとき、ある参加者に対するEの勝率はロジスティック分布で近似することができるだろうと考えるのは妥当なことである。
つまり、以下である。
\begin{align*}
E\text{の勝率} =& \frac{1}{1 + e^\frac{E\text{との内部レート差} \hspace{1.5em}}{s}}
\end{align*}
$s$の値は実際なんでもよい。
つまり、AtCoder社が、内部レート差がいくつならば勝率はいくつであるべきと考えるかの匙加減によって決まる。
もっと言うと、$s$はレート4000という数字の価値を紙屑とするか素晴らしいものとするかを決めるパラメータである。
AtCoder社は$s$の値を$\frac{400}{\log 6}$とした。
すなわち、内部レート差200のとき内部レートが高い側の勝率は約71%である。
勝率同士は独立なので、勝率を足していくと勝ち数の期待値を求めることができる。
つまり、以下である。
\begin{align*}
E\text{の勝ち数の期待値} =& \sum_{u \in E\text{を除く全参加者} \hspace{2em}} \frac{1}{1 + e^\frac{E\text{と}u\text{の内部レート差} \hspace{1.5em}}{s}}
\end{align*}
さて、実際のEの勝ち数は引き分けを0.5勝と考えることにすると1.5勝だったわけである。
すると、1.5勝が期待値になるようなEの内部レートを求めることができる。
これすなわちEの内部レートの最も尤もらしい値である。
\begin{align*}
1.5 =& \frac{1}{1 + e^\frac{1500 - x}{\frac{400}{\log 6}}} + \frac{1}{1 + e^\frac{1600 - x}{\frac{400}{\log 6}}} + \frac{1}{1 + e^\frac{1700 - x}{\frac{400}{\log 6}}} + \frac{1}{1 + e^\frac{1800 - x}{\frac{400}{\log 6}}}\\
x =& 1529.0143956607496 \ldots\\
\end{align*}
最後に、Eの内部レートの最も尤もらしい値を求める式が、Cの内部パフォーマンスを求める当初の定義式と一致することを確認しておこう。
一般に、新たな参加者の内部レートを$x$、新たな参加者の勝ち数の期待値を$w$、既存のRatedな参加者の内部レートをそれぞれ$a_1, a_2, \ldots, a_n$とすると、
\begin{align*}
w =& \sum_{i=1}^n \frac{1}{1 + e^\frac{a_i - x}{\frac{400}{\log 6}}}\\
w =& \sum_{i=1}^n \frac{1}{1 + 6^\frac{a_i - x}{400}}\\
n - w =& n - \sum_{i=1}^n \frac{1}{1 + 6^\frac{a_i - x}{400}}\\
n - w =& \sum_{i=1}^n \left(1 - \frac{1}{1 + 6^\frac{a_i - x}{400}}\right)\\
n - w =& \sum_{i=1}^n \frac{1}{1 + 6^\frac{x - a_i}{400}}\\
\end{align*}
$n - w$は定義より、$w$の値を決めるのに使った既存のRatedな参加者のFractional Rankingでの順位 - 0.5と一致する。
証明終わり。
例外規定: AtCoder Grand Contest 001の場合
細かい話だが、実はAtCoder Grand Contest 001だけは内部パフォーマンスの計算手順が微妙に異なる。
というのも、AtCoder Grand Contest 001は、AtCoderの現在のレーティングシステムが始まった最初のコンテストだからである。
想像してみればわかることかと思うが、AtCoder Grand Contest 001開始前時点ではすべての参加者にはレートが付いておらず、また従って、すべての参加者の内部レートは1600扱いであった。
これでは内部パフォーマンスが1600付近に集中してしまう(具体的には優勝者の内部パフォーマンスが3285にしかならない)ので、AtCoder Grand Contest 001だけは通常の内部パフォーマンス計算手順の後にアドホックな補正が入る。
\begin{align*}
\text{補正後内部パフォーマンス} &= (\text{補正前内部パフォーマンス} - 1600) \times 1.5 + 1600
\end{align*}
見ての通り、1600との差分を強調する補正である。
補正後では、優勝者の内部パフォーマンスは4128になる。
レートの算出
レートは、パフォーマンスを集計したものであり、レートの4つの性質を満たすような集計方法を採用している。
具体的な集計方法を説明する。
性質1: 大成功を重視
(多分ユーザーのモチベーションのために)大成功を相対的に高い重要度で評価し、大失敗を相対的に低い重要度で評価する
段階的に考えていくため、性質2(新しいコンテストの結果を重視)はいったん無視する。
そのように考えたとき、パフォーマンスを集計する最も素直な方法は相加平均であるので、相加平均をベースに考えていく。
さて、あるユーザーがパフォーマンス800, 1600, 2400をとったとする。
このユーザーは平均1600のパフォーマンスを出せるわけだが、800はそこまで低くなく、そして2400は高く評価してあげたい。
どのようにパフォーマンスを集計すべきか?
答えは指数関数で写像した空間で相加平均をとることである。
つまり、
| 通常の空間におけるパフォーマンス | 指数関数で写像した空間におけるパフォーマンス |
|---|---|
| 0 | 1 |
| 800 | 2 |
| 1600 | 4 |
| 2400 | 8 |
| 3200 | 16 |
| 4000 | 32 |
このようにマッピングしていく。
すると、2400の重要度が相対的に高く、800の重要度が相対的に低くなるのである。
\begin{align*}
\frac{2 + 4 + 8}{3} =& \frac{14}{3}
\end{align*}
このままだと意味が分からない数字になってしまうので最後に逆写像する。
| 通常の空間におけるパフォーマンス | 指数関数で写像した空間におけるパフォーマンス |
|---|---|
| 0 | 1 |
| 800 | 2 |
| 1600 | 4 |
| 1777.9139370691585… | 14/3 |
| 2400 | 8 |
| 3200 | 16 |
| 4000 | 32 |
今の計算方法を式として書き直すと以下のようになる。
\begin{align*}
\text{レート(第一段階)} =& 800 \log_2\left(\frac{\sum_{p \in \text{全パフォーマンス}} \hspace{2em} 2^\frac{p}{800}}{\text{Ratedなコンテストへの参加回数}}\right)
\end{align*}
性質2: 新しいコンテストの結果を重視
新しいコンテストの結果を相対的に高い重要度で評価し、古いコンテストの結果を相対的に低い重要度で評価する
新しいコンテストの結果を重視するには、レート(第一段階)を求める式中の相加平均をそのまま重みつき平均に変えればよい。
つまり、
\begin{align*}
\text{レート(第二段階)} =& 800 \log_2\left(\frac{\sum_{i=1}^\text{Ratedなコンテストへの参加回数} 2^\frac{\text{新しい方から}i\text{番目のパフォーマンス}}{800} \times 0.9^i}{\sum_{i=1}^\text{Ratedなコンテストへの参加回数} 0.9^i}\right)
\end{align*}
性質3: リセマラ対策
あるユーザーが初参加のコンテストで失敗した場合、最初のコンテスト結果に引きずられてレートが伸び悩むのを防ぐためにアカウントを作り直そうとそのユーザーが考えることがない
これは、Ratedなコンテストへの参加回数が少ないほど値が大きくなるリセマラ対策補正9を導入することで解決する。
\begin{align*}
\text{レート(第三段階)} =& \text{レート(第二段階)} - \text{リセマラ対策補正}
\end{align*}
リセマラ対策補正の値は具体的には以下である。
| Ratedなコンテストへの参加回数 | リセマラ対策補正 |
|---|---|
| 1 | 1200 |
| 2 | 745.4132091674061… |
| 3 | 545.1360660734733… |
| 4 | 426.73183189445916… |
| 5 | 346.81280099957957… |
| 6 | 288.6207613158372… |
| 7 | 244.12623521104518… |
| 8 | 208.93228764736375… |
| 9 | 180.39932641532823… |
| 10 | 156.83200284236497… |
| … | … |
| 15 | 82.98902775369456… |
| … | … |
| 20 | 46.42901326444941… |
| … | … |
| 30 | 15.479721309519988… |
| … | … |
| 50 | 1.8460065772594954… |
| … | … |
| ∞ | 0 |
式として表すと以下になる。
\begin{align*}
\text{リセマラ対策補正} &= \frac{\frac{\sqrt{1 - 0.81^\text{Ratedなコンテストへの参加回数}}}{1 - 0.9^\text{Ratedなコンテストへの参加回数}} - 1}{\sqrt{19} - 1} \times 1200
\end{align*}
私はリセマラ対策補正がなぜこのような形の式になるのか理解できていないので、説明もできない。
追記(2018/7/31): chokudai社長によるコメント
レート計算式に関する記事があった。「リセマラ対策」と書かれている部分は、厳密には、「参加回数が少ないと信頼度が足りないから低めに出る」って感じ。
— chokudai(高橋 直大) (@chokudai) 2018年7月31日
AtCoderのレート計算式 https://t.co/nnDj6SuaRX
追記(2018/8/9): 「リセマラ対策補正」がどういう仮定の下であの形になるのか考えたけどできなかったという話
「リセマラ対策補正」とした項がリセマラ対策になるのは副次的な効果であって、chokudai社長のコメントにもある通り、本来この項は、レートを99.9%実力保証値とするために導入された、と考える方が正しいようである。
ところが考えをまとめるために数式をいじっていたら、レートが99.9%実力保証値であるというそもそもの前提が、ある仮定の下では崩れるのではないかという疑念が出てきた。
ある仮定の下でAtCoderのレートは99.9%実力保証値ではないことの証明(仮)
これは要するに、この項の意味を説明するためにはこのような仮定が存在しなければならないだろうと私が予想した仮定が、実際には誤っていたのではないかということを示す。
AtCoder社がどのような仮定をおいてレートを99.9%実力保証値であると主張しているのか、そしてその仮定からどのようにこの項が導かれるのか、ご存知の方は教えてください。
性質4: 初心者への慈悲
(多分初心者のモチベーションのために)初心者のレートが例えばマイナスのような低すぎる値になってしまうことがない
これは、400以下のレートを以下のようにマッピングすることで解決する。10
| レート(第三段階) | レート(第四段階) |
|---|---|
| 400 | 400 |
| 0 | $\frac{400}{e}$ |
| -400 | $\frac{400}{e^2}$ |
| -800 | $\frac{400}{e^3}$ |
| … | … |
| -∞ | 0 |
式で表すと以下である。
\begin{align*}
\text{レート(第四段階)} =& \left\{\begin{array}{ll}
\frac{400}{e^\frac{400 - \text{レート(第三段階)} \hspace{1em}}{400}} & \text{if}\,\text{レート(第三段階)} \leq 400\\
\text{レート(第三段階)} & \text{otherwise.}\\
\end{array}\right.\\
\end{align*}
最終段階: 整数化
レートは整数なので最終的に四捨五入する。
\begin{align*}
\text{レート} =& \left\lfloor\text{レート(第四段階)} + 0.5\right\rfloor\\
\end{align*}
まとめ
- パフォーマンスの上限なし版が内部パフォーマンス
- これまでの内部パフォーマンスから内部レートが計算できる
- Ratedな参加者の内部レート分布とコンテストでのRated参加者内順位から内部パフォーマンスが計算できる(そしてもちろんパフォーマンスも計算できる)
- これまでのパフォーマンスからレートが計算できる
- レートが満たす4つの性質
- 大成功を重視
- 新しいコンテストの結果を重視
- リセマラ対策
- 初心者への慈悲
-
後述するが、レートに関しては言えないだけで、言えるような内部的な数字はある。 ↩
-
原文では四捨五入とは明示されていないものの、AtCoderの実際の実装は四捨五入になっている。
各計算手順の詳細は「レートの算出」節で後述する。 ↩ -
「内部パフォーマンス」は私が説明のために便宜的に作った言葉で、原文では「Perf」と呼ばれている。 ↩
-
「内部レート」は私が説明のために便宜的に作った言葉で、原文では「APerf」と呼ばれている。
これらの値は基本的に公開されておらず、パフォーマンスの計算のためだけに用いられる。
役割分担としては、(おそらくは内部パフォーマンスと内部レートの方が数学的な扱いが容易であるために)基本は内部パフォーマンスと内部レートをベースに計算処理を行い、実際のパフォーマンスは内部パフォーマンスを加工して表示するようにしている。
レートは、パフォーマンスをさらに概要で説明したように集計して得られる。 ↩ -
原文では実数であるとは明示されていない。ac-predictorは実数として扱っているが大きな矛盾は無いようである。
内部レートは新しい内部パフォーマンスの方が大きな重みを持つように平均をとったものである。 ↩ -
「デフォルト内部レート」は私が説明のために便宜的に作った言葉で、原文では「Center」と呼ばれている。 ↩
-
原文では四捨五入とは明示されていないものの、AtCoderの実際の実装は四捨五入になっている。 ↩
-
「リセマラ対策補正」は私が説明のために便宜的に作った言葉で、この記事以外では使われていない。 ↩
-
実は原文にはこの計算手順は書かれていないが、AtCoderの実際の実装には明らかにこの手順が存在する。 ↩