正答率・再現率・特異度・適合率・偽陽性率・偽陰性率・F値まとめ

#はじめに
題名にある通り正答率(正解率)、再現率、特異度、適合率、偽陽性率、偽陰性率、F値について、算出方法に焦点を絞って備忘録を兼ねたまとめを書きたいと思います。
機械学習や物体検出手法、診断などの世界では精度の評価指標としてよく用いられると思うので、よかったら算出方法の備忘録として覗いてください。

#全体像

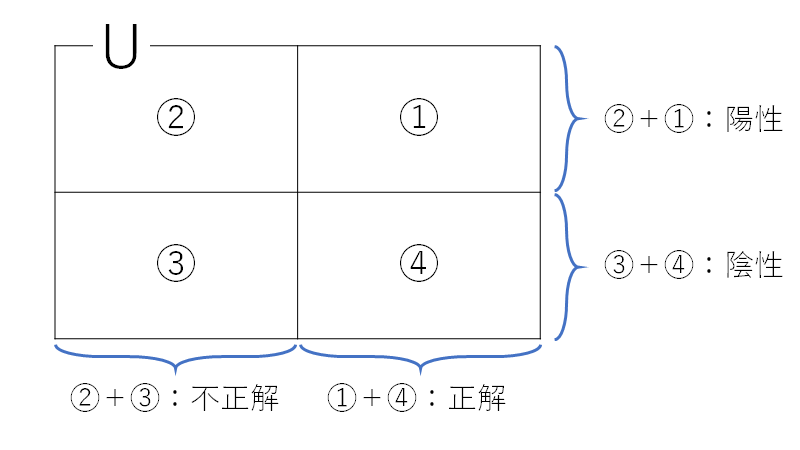
全体像を図にするとこんな感じです。

##上の図の説明

• とあるクラスにサンプルたちが入るか入らないかという分類問題をした状況を想定する。
• 分類したサンプルたちをすべて含めた集合をUとしている。
  • ①：「このサンプルはとあるクラスに入っている」と判断された、かつその判断は正しかった
  • ②：「このサンプルはとあるクラスに入っている」と判断された、かつその判断は間違っていた
  • ③：「このサンプルはとあるクラスに入っていない」と判断された、かつその判断は間違っていた
  • ④：「このサンプルはとあるクラスに入っていない」と判断された、かつその判断は正しかった

##蛇足
「陽性や陰性って何？」といった内容を具体例と混ぜて説明します。不要な方は読み飛ばしてください。

• 病気にかかっているかを診断する状況を具体例として考える。
  • この場合は「病気にかかっている人たち」というのが「とあるクラス」に該当する。
  • ①：「この人は病気にかかっている」(このサンプルはとあるクラスに入っている)と判断された、かつその判断は正しかった
  • ②：「この人は病気にかかっている」(このサンプルはとあるクラスに入っている)と判断された、かつその判断は間違っていた
  • ③：「この人は病気にかかっていない」(このサンプルはとあるクラスに入っていない)と判断された、かつその判断は間違っていた
  • ④：「この人は病気にかかっていない」(このサンプルはとあるクラスに入っていない)と判断された、かつその判断は正しかった
• 陽性とは：「この人は病気にかかっている」(このサンプルはとあるクラスに入っている)と判断することを陽性と言う
• 陰性とは：「この人は病気にかかっていない」(このサンプルはとあるクラスに入っていない)と判断することを陰性と言う
  • でも陽性や陰性と判断してもやっぱり間違いがあるため、それが正解とか不正解になる
    • 「この人は病気にかかっている」と判断しても「実はかかっていなかった」(このサンプルはとあるクラスに入っていなかった)などの状況が該当
• 正解とは：陽性、もしくは陰性の判断が正しかったこと
• 不正解とは：陽性、もしくは陰性の判断が間違っていたこと
• 実際に「病気にかかっている人たち」は①+③
• 実際には「病気にかかっていない人たち」は②+④

#算出方法
##正答率(正解率)
全サンプルの中で、診断が正しかったサンプル数

正答率 = \frac{①+④}{①+②+③+④} 

##再現率
実際は陽性だったサンプルの中で、陽性という判断が正しかかった数

再現率 = \frac{①}{③+①} 

##特異度
陰性と判断したサンプルの中で、陰性という判断が正しかった数

特異度 = \frac{④}{③+④} 

##適合率
陽性と判断したサンプルの中で、陽性という判断が正しかった数

適合率 = \frac{①}{②+①} 

##偽陽性率
陽性と判断したサンプルたちの中で、判断が間違っていたサンプル数

偽陽性率 = \frac{②}{①+②} 

##偽陰性率
陰性と判断したサンプルたちの中で、判断が間違っていたサンプル数

偽陰性率 = \frac{③}{③+④} 

##F値
再現率と適合率の調和平均

F値 = 2 \times \frac{再現率 \times 適合率}{再現率+適合率}