はじめに
ニューラルネットワークは、その予測値とデータセットにより与えられる真の値の差が最も小さくなるような重みパラメータを決定することで学習されます。この差を表す関数を「損失関数」といい、一般的に、線形回帰では最小二乗誤差、ロジスティック回帰では交差エントロピーが用いられます。ところで、これらの損失関数はどのように得られた式なのでしょうか?そんな疑問にお答えするために、今回は線形回帰における損失関数を導出していきます。
最尤推定とは
最尤推定とは、未知の確率分布$P(·)$を推定するために、パラメータ$\theta$による仮説的な確率分布$Q(·|\theta)$を用いて、データが得られる確率が尤もらしくなるような$\theta$を求める手法のことです。
これをニューラルネットワークに当てはめると、$P(·)$はデータセットにより与えられる真の値の確率分布、パラメータ$\theta$はニューラルネットワークの重み、$Q(·|\theta)$はニューラルネットワークが出力する予測値の確率分布になります。つまり、ニューラルネットワークにおける最尤推定とは、真の値の確率分布を尤もらしく近似するような予測値の確率分布を決定するためのパラメータ$\theta$(重み)を求めるアプローチであると考えることができます。
具体的には、データ$x$が同一分布から独立に得られると仮定すると、このときの同時確率を
L(x|\theta) = \prod_{i=1}^{n} Q(x_i|\theta) \tag{1}
と書き、これを最大化するような$\theta$を求めます。
なお、このときの$L(x|\theta)$を尤度(Likelihood)と呼びます。
同時確率とは、事象Aと事象Bが同時に発生する確率のことです。期待するニューラルネットワークは、あらゆる入力値に対してそれぞれ正しい予測値を出力するという事象が同時に発生する必要があるため、すべてのデータに対する同時確率を最大化することを考えます。
最尤推定では、尤度の最大化がしばしば複雑になるため、対数をとった対数尤度(総乗が総和に変換される)の最大化や、負の対数尤度の最小化を考えることが一般的です。
線形回帰における最尤推定
それでは、最尤推定を用いて線形回帰の損失関数を導出していきましょう。
線形回帰とは、あるデータセット$D = {(x_1,t_1),(x_2,t_2),...,(x_n,t_n)}$が与えられたとき、$x$と$t$の関係を
y = f(x) = w_0+w_1x \tag{2}
のような、パラメータ$w$に関して線形な式で表現する手法のことです。
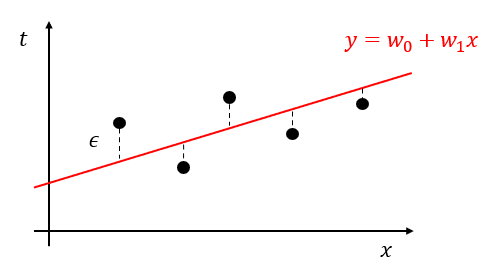
このとき、$x$に対する真の値$t$と予測値$y$の関係は、式$(2)$と誤差$\epsilon$を用いて
t = y+\epsilon = w_0+w_1x+\epsilon \tag{3}
で表すことができます。
ここで、データセット$D$が十分に大きいとき、$t$をうまく予測できる$y$は、誤差$\epsilon$が$\epsilon = 0$付近に多く集中する(一方、誤差$\epsilon$の絶対値が大きいデータの数は、誤差$\epsilon$の絶対値が大きくなるにつれて減少する)ため、$\epsilon$は平均$0$、分散$\sigma^2$の正規分布に従うと仮定できます。
\epsilon \sim N(0,\sigma^2) \tag{4}
さらに、式$(3)(4)$より、$\epsilon=t-(w_0+w_1x)$が正規分布$N(0,\sigma^2)$に従うため、$t$は平均$w_0+w_1x$、分散$\sigma^2$の正規分布に従うことがわかります。
t \sim N(w_0+w_1x,\sigma^2) \tag{5}
これより、入力$x$を与えたときに出力$t$が得らえる確率分布は
q(t|x;w,\sigma) = \frac{1}{\sqrt{2\pi\sigma^2}} \exp \Biggl(-\frac{\bigr(t-(w_0+w_1x)\bigr)^2}{2\sigma^2}\Biggl) \tag{6}
となり、
L(t|x;w,\sigma) = \prod_{i=1}^{n} \frac{1}{\sqrt{2\pi\sigma^2}} \exp \Biggl(-\frac{\bigr(t_i-(w_0+w_1x_i)\bigr)^2}{2\sigma^2}\Biggl) \tag{7}
を最大化すればよいことになります。
しかし、このまま式$(7)$を最大化することは難しいので、負の対数尤度を最小化することを考えます。
-\log L(t|x;w,\sigma) = -\sum_{i=1}^{n} \log \frac{1}{\sqrt{2\pi\sigma^2}} \exp \Biggl(-\frac{\bigr(t_i-(w_0+w_1x_i)\bigr)^2}{2\sigma^2}\Biggl) \tag{8}
それでは実際に計算してみましょう。
まずは、式$(8)$の右辺、シグマの中の項を次のように変換します。
\begin{align}
\log \frac{1}{\sqrt{2\pi\sigma^2}} \exp \Biggl(-\frac{\bigr(t_i-(w_0+w_1x_i)\bigr)^2}{2\sigma^2} \Biggl) &= \log {\frac{1}{\sqrt{2\pi\sigma^2}} + \log \exp \Biggl(-\frac{\bigr(t_i-(w_0+w_1x_i)\bigr)^2}{2\sigma^2}\Biggl)} \\
&= C + \Biggl(-\frac{\bigr(t_i-(w_0+w_1x_i) \bigr)^2}{2\sigma^2}\Biggl) \\
&= C + C' \Bigr(-\bigr(t_i-(w_0+w_1x_i)\bigr)^2\Bigr)
\end{align}
- 対数法則により、積を和に分解します。
- $\frac{1}{\sqrt{2\pi\sigma^2}}$は定数項であるため、$C$に置き換えます。
- 対数関数と指数関数の関係($\log \exp(x)=x$)より、第2項を変換します。
- $2 \sigma^2$は定数であるため、$C'$に置き換えます。
この変換を用いて式$(8)$を整理すると
-\log L(t|x;w) = -\sum_{i=1}^{n} C + C' \Bigr(-\bigr(t_i-(w_0+w_1x_i)\bigr)^2\Bigr) \tag{9}
となり、最小化において定数項は無視できるため
\begin{align}
-\log L(t|x;w) &= \sum_{i=1}^{n} \bigr(t_i-(w_0+w_1x_i)\bigr)^2 \\
&= \sum_{i=1}^{n} (t_i-y_i)^2 \tag{10}
\end{align}
を最小化すればいいことになります。
式$(10)$は真の値$t_i$と予測値$y_i$の二乗誤差の総和の形になっており、二乗誤差の総和の最小化(=最小二乗誤差)が尤度を最大にするパラメータ$w$の推定になっていることがわかります。これより、線形回帰における損失関数、最小二乗誤差が導出できました。
おわりに
今回は、最尤推定により線形回帰における損失関数、最小二乗誤差を導出しました。次回は、最尤推定を用いてロジスティック回帰における損失関数を導出します。