はじめに
この記事は、以下の内容の続きになります。
ロジスティック回帰における最尤推定
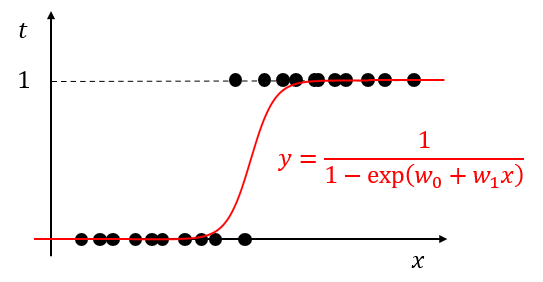
ロジスティック回帰とは、あるデータセット$D={(x_1,t_1),(x_2,t_2),...,(x_n,t_n)}, t_i \in \set{0,1}$が与えられたとき、$x$と$t$の関係を
y = f(x) = \frac{1}{1-\exp(w_0+w_1x)} \tag{1}
により表現する手法のことです。
ここで、入力$x$を与えたときにラベル$t$を得る確率分布は、$t=0$を正しく予測する事象と$t=1$を正しく予測する事象の同時確率であるため、式$(1)$を用いて
q(t|x) = q(t=1|x)^t q(t=0|x)^{1-t} = \bigr(f(x)\bigr)^t \bigr(1-f(x)\bigr)^{1-t} \tag{2}
で表すことができ
L(t|x;w) = \prod_{i=1}^n \bigr(f(x_i)\bigr)^{t_1} \bigr(1-f(x_i)\bigr)^{1-t_1} \tag{3}
を最大化すればよいことになります。
$t=1$のとき、$q(1|x) = q(t=1|x)^1 q(t=0|x)^{1-1} = q(t=1|x) = f(x)$
$t=0$のとき、$q(0|x) = q(t=1|x)^0 q(t=0|x)^{1-0} = q(t=0|x) = 1-f(x)$
しかし、このまま式$(3)$を最大化することは難しいので、負の対数尤度を最小化することを考えます。
- \log L(t|x;w) = - \sum_{i=1}^n \log \bigr(f(x_i)\bigr)^{t_1} \bigr(1-f(x_i)\bigr)^{1-t_1} \tag{4}
それでは実際に計算してみましょう。
まずは、式$(4)$の右辺、シグマの中の項を次のように変換します。
\begin{align}
\log \bigr(f(x_i)\bigr)^{t_1} \bigr(1-f(x_i)\bigr)^{1-t_1} &= \log \bigr(f(x_i)\bigr)^{t_1} + \log \bigr(1-f(x_i)\bigr)^{1-t_1} \\
&= t_i \log \bigr(f(x_i)\bigr) + (1-t_i) \log \bigr(1-f(x_i)\bigr) \\
\end{align}
この変換を用いて式$(4)$を変換すると
- \log L(t|x;w) = - \sum_{i=1}^n t_i \log \bigr(f(x_i)\bigr) + (1-t_i) \log \bigr(1-f(x_i)\bigr) \tag{5}
が得られ、これを最小化すればよいことになります。
式$(5)$は、一般的に(二値)交差エントロピーと呼ばれ、ロジスティック回帰における(二値)交差エントロピーの最小化は、尤度を最大にするパラメータ$w$の推定になっています。これより、ロジスティック回帰における損失関数、交差エントロピーが導出できました。
おわりに
今回は、最尤推定によりロジスティック回帰における損失関数「交差エントロピー」を導出しました。これまで「最小二乗誤差」「交差エントロピー」と比較的簡単な損失関数について触れてきましたが、今後は複雑な損失関数が最尤推定で設計されている事例についても調べてみたいと思います。