こんにちは!
新卒エンジニアの宮内です。
アニさんというニックネームは中学生の頃に親友に付けてもらいまして。クラスメイト全員にアニメを見てもらうことを目標に布教活動をしている時に付けてもらいました。我ながら何を目指してたんでしょうか。
アドベントカレンダーが終わったらクーリッシュに改名しようと思います。僕は人生通して何を目指してるんでしょうか。(クーリッシュの元ネタはこちら)
アドベントカレンダー22日目ということで、DeepLearning勉強し始めた当時の自分が欲しかった記事を書こうと思います。
背景的な
もうすでに人工知能(AI)や機械学習、DeepLearningについて詳しく説明している記事は数多くあります。
ただ、現状見かける記事のレベル感って
- 極端に表面的である
- 極端に専門的である
のどちらかだと思ってます。興味を持って踏み込んで見ると、数学の知識や複雑に見えるロジックを目の当たりにして諦めてしまう人が多いと思うんですよね。
筋トレで言うと、「ダンベルが10Kgと60Kgしか置いてないから、60Kgに到達する前に興味なくしちゃう」みたいなイメージだと思ってます。(急に60Kgなんて上げる気にもならないっすよね...w)
そして、ここに大きな壁があると感じています。
そこで、ダンベル30Kgくらいの負荷で勉強できる記事を書こうってのが、この記事のコンセプトです。
(最後に40Kgくらいの負荷も用意してます)
DeepLearningの正体
DeepLearningを理解するには以下の3点を理解して、前提知識を付ければOKです!!
- パーセプトロン
- ニューラルネットワーク
- 重み
この3つが分かればDeepLearningの学習にすんなり入れます!
さっそくパーセプトロンいきましょー!
パーセプトロン
まずは抽象的に理解しましょう!
ハンバーガーを作って、美味しい・美味しくないを判断するとします。
材料を以下の2つとしましょう。
- バンズ
- パティ
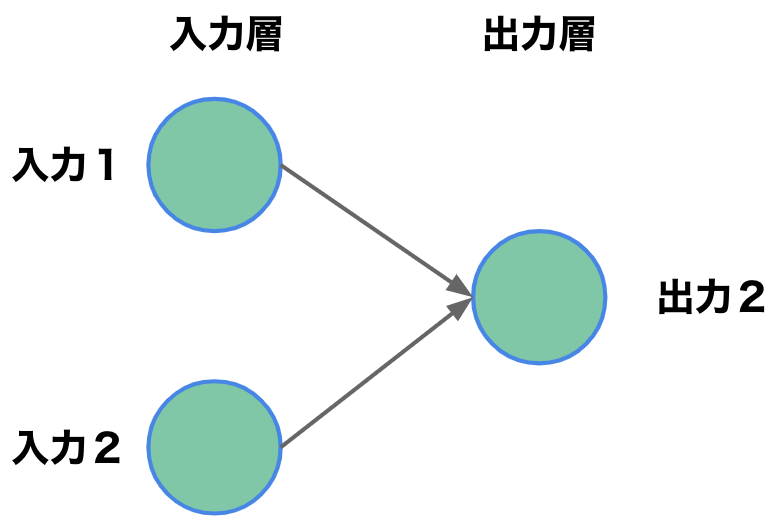
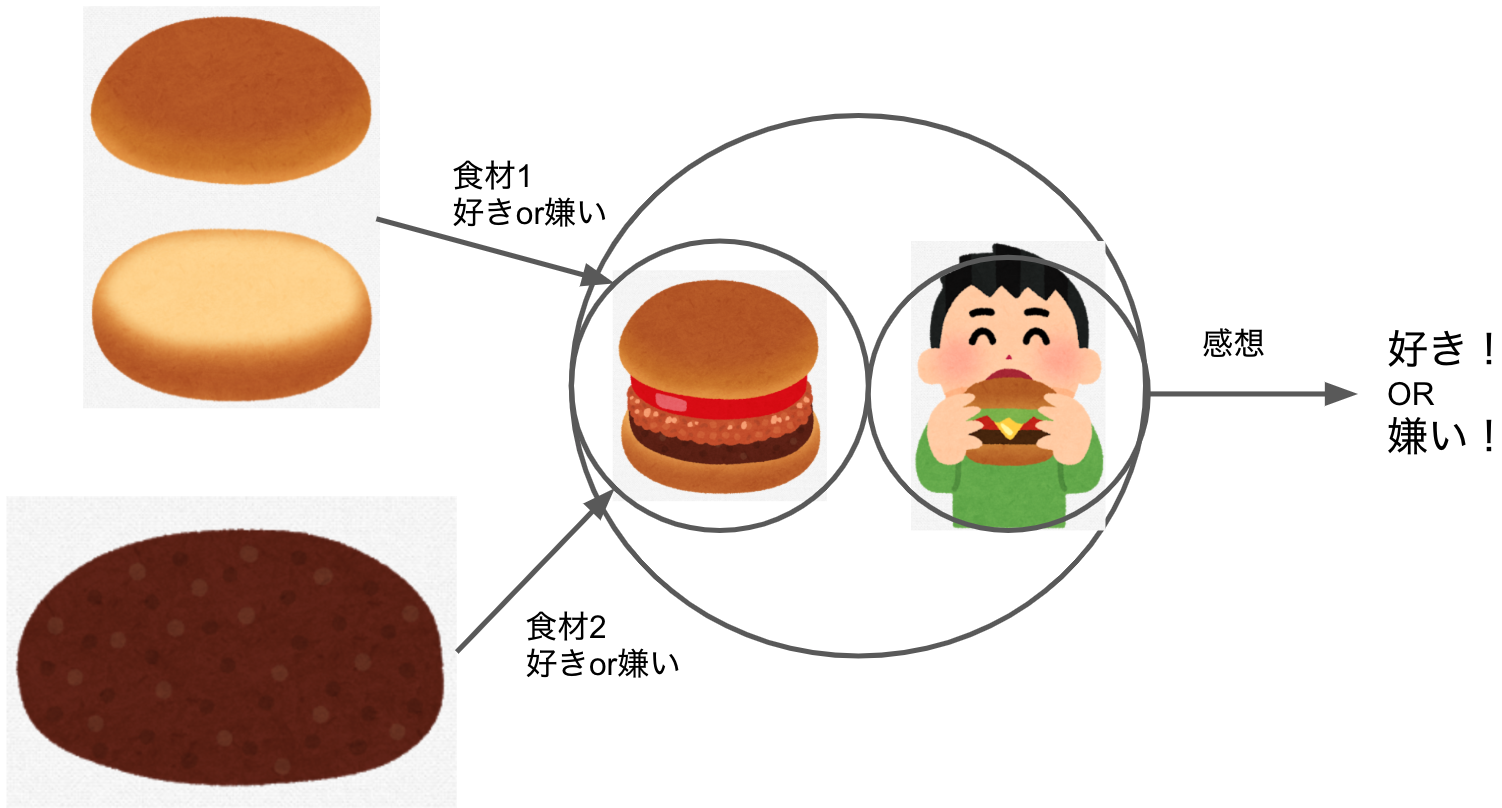
2つの食材を使ったハンバーガーが美味しいかどうかをパーセプトロンで表現するとこんな感じになります。
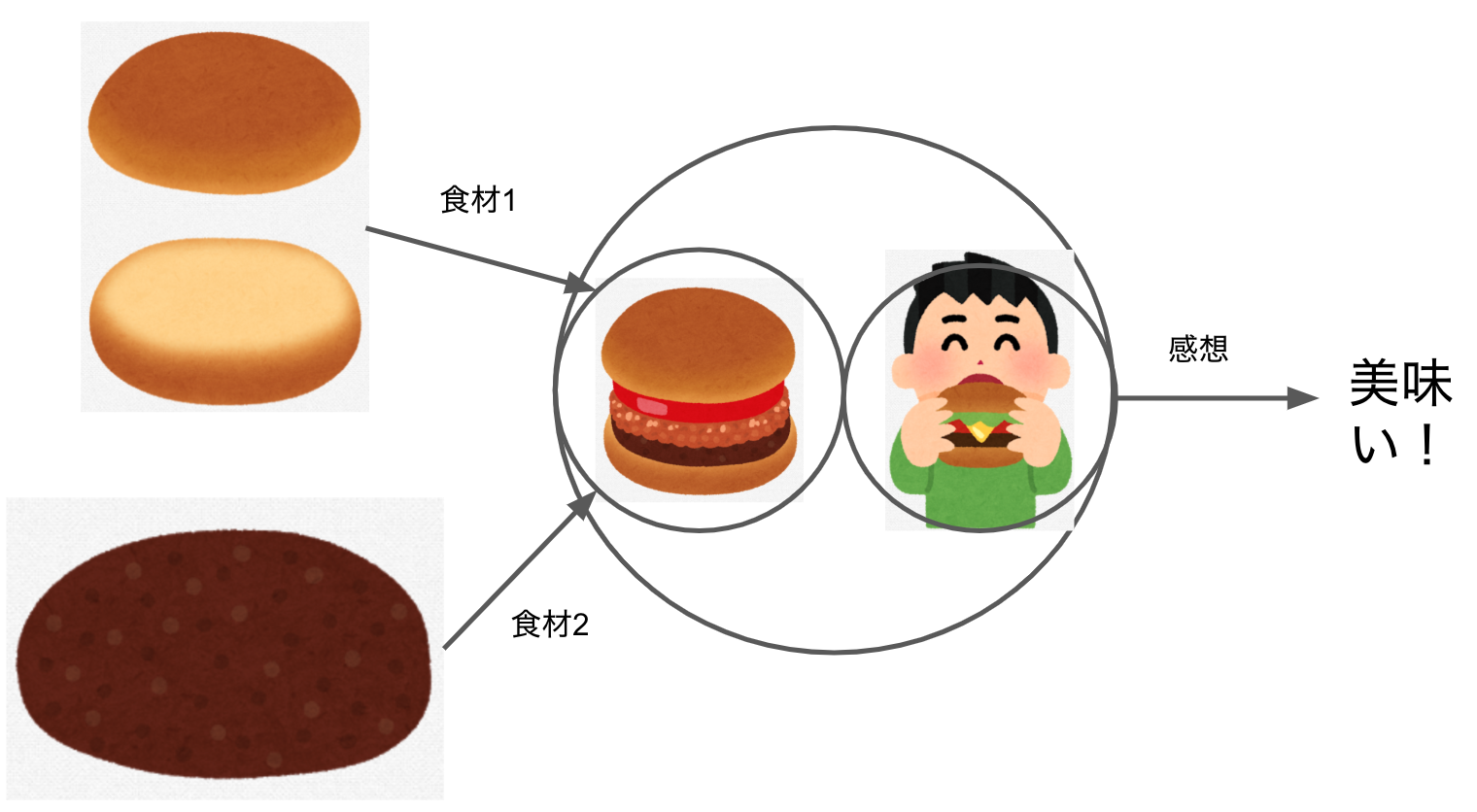
要するにパーセプトロンは2つの入力に対して1つの出力を返します。
ここで注目して欲しいのは、食べた感想が人によって変わってくる点です。
ここで、バンズかパティが出来上がるわけじゃないってところも実は肝だったりするのでこの感覚は、引き続き持っておいて欲しいです。
ではイメージを持ったところで、具体的に説明していきます。
具体的な数字で説明
このパーセプトロンは美味しさが0.8以上だと、美味しい(出力1)であるとします。
0.8というのは判断の境目、すなわち閾値と呼ばれるものです。非常に重要な単語なので頭に入れといてください。
計算式は入力をx, 出力をzとすると
z = x1 * 0.5 + x2 * 0.5
で表されます。(論理回路で言うAND)
(例) [x1, x2] = [1, 0] の場合 1 × 0.5 + 0 × 0.5 = 0.5 出力は 0.5 < 0.8 なので '0'となりますね
なので、全パターンを表にすると以下のようになります
| 入力1 | 入力2 | 出力(0.8以上なら1) |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
今回のケースだと[x1, x2] = [1, 1]以外は全部'0'となります。
これ人間が物事を判断するロジックと似ているんですね。
先ほどのハンバーガーの例に当てはめてみましょう。
パーセプトロンは脳の一部
食材それぞれの入力を[好き, 嫌い]=[1, 0]であるとします。
| 食材1 | 食材2 | 感想(0.8以上なら1) |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 0 | 0 |
| 0 | 1 | 0 |
| 1 | 1 | 1 |
今回のパーセプトロン君はどちらの食材も好きじゃないと、「美味しい!」って言わないわけですね。このようにパーセプトロンは2つの入力に対して1つの結果を返すわけですが、これで人工知能とは言えないですね。
なぜかというと、人の「美味しい」という判断は食材だけで決まっているわけではないからです。
- 味付け
- 歯応え/食感
- 量
- 一緒に食べる人
などなど、いろいろな要素が合わさっての「美味しい」だと思います。
次に説明するニューラルネットワークは、パーセプトロンを進化させて判断に対する複雑な要素を組み合わせて判断をできるものです。
ニューラルネットワーク
ニューラルネットワークの理解はパーセプトロンを理解できた方にとっては非常に簡単です。
この項目では「重み」というものを理解していきましょう
パーセプトロンで少しイメージは出来ていると思うので、いきなり具体的な説明をしていきます。
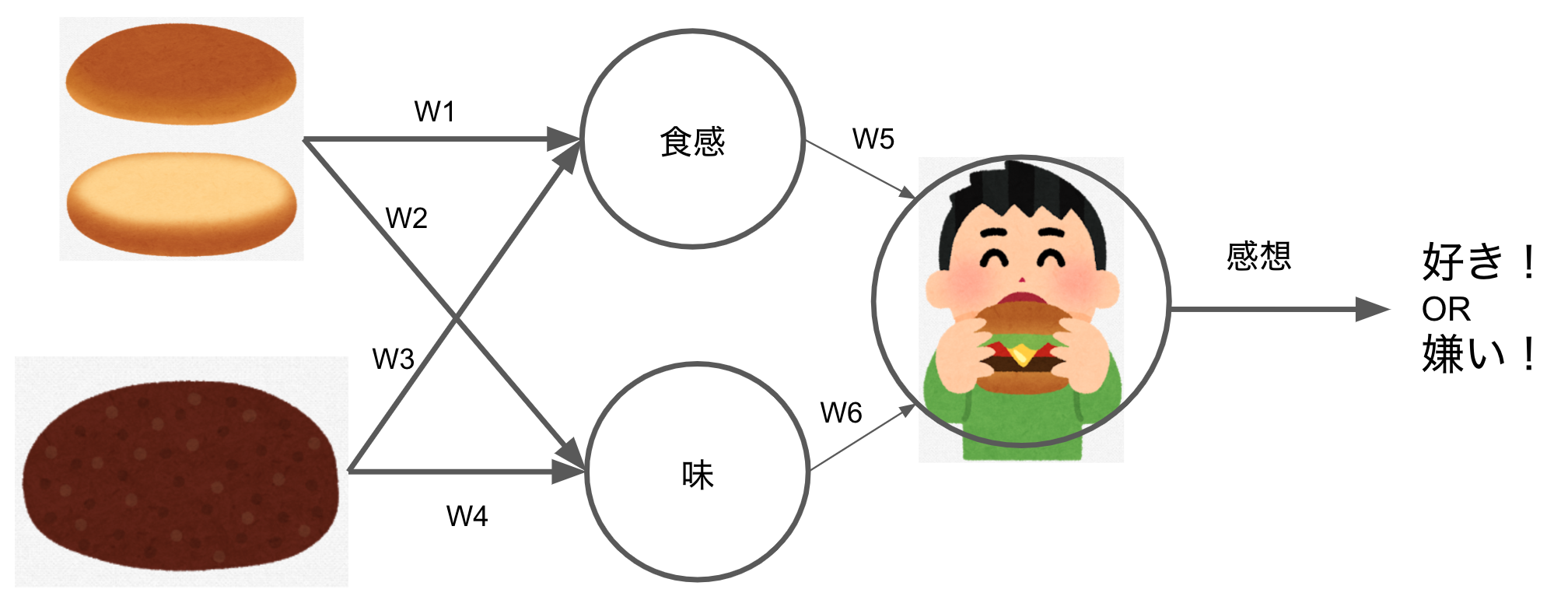
また同じ材料からハンバーガーを作って、食べた感想を出力するニューラルネットワークを見てみましょうここでは話を単純にするために3階層にします。
ハンバーガーには食感と味付けが存在しますが、それぞれバンズとパティの両方の食感・味が合わさってるわけです。
しかし、バンズとパティが食感と味付けそれぞれに等しく影響している訳ではないですよね。
これが重みです。
ハンバーガーの美味しさに対して
[食感]
バンズ : パティ = 7 : 3
[味]
バンズ : パティ = 2 : 8
の割合で影響していると仮定すると、W1〜W4を
[W1, W2, W3, W4] = [0.7, 0.3, 0.2, 0.8]
のように表現できるわけです。
さらに、「美味しいかどうかの判断」に食感と味が
[美味しいかどうか]
食感 : 味 = 6 : 4
の割合で影響していると仮定するとW5,W6は
[W5, W6] = [0.6, 0.4]とすることができます。
閾値はそれぞれ
食感:0.5
味:0.4
美味しいかどうか:0.55
とします。これを超えたら'1'を出力するわけです。
ニューラルネットワークは脳の判断ロジックそのもの
計算のしかたはシンプルです。
z = (入力1) * (1に対する重み) + (入力2) * (2に対する重み)
[x1, x2] = [1, 0]として、順に計算していきましょう。
[食感]
z = 1 * 0.7 + 0 * 0.2
= 0.7
→ 0.5 < 0.7 なので '1'を出力
[味]
z = 1 * 0.3 + 0 * 0.8
= 0.3
→ 0.4 > 0.3なので '0'を出力
[食感, 味] = [1, 0]であることが分かりました。
以上の2つを入力として美味しいかどうか判断しましょう。
[美味しいか]
z = 1 * 0.6 + 0 * 0.4
= 0.6
→ 0.55 < 0.6 なので'1'を出力
すなわち・・・美味しい!!という判断になります。
このように入力に対して重みをつけることによって、判断をより細かく正確にしていきます。
しかしこれ・・・閾値と重みの値設定で大きく結果が変わることにお気づきでしょうか・・・?
今回は3階層しかないので、手で簡単に計算をしていきました。しかし、より複雑な判断ロジックになっていくと重み・閾値の設定などが非常に多くなり、人間が判断できるレベルを超えてきます。ハンバーガーの例で言うと食材が100にも10000にもなるイメージです。
DeepLearningとは何か
ズバリ答えを出すと、
多層なニューラルネットワークの適切な閾値・重みパラメーターを導き出すための学習手法です。
閾値・重み、バイアス(今回は出てませんがDeepLearningの理解には必須です)の初期値を決めてあげれば、あとは機械学習を行うことで、最適なパラメーターを求めていく仕組みです。
DeepLearningで学ぶことは、
- ミニバッチとその理由、適切な抽出数
- 勾配を用いたパラメーターの更新
- パラメーター処理を軽くするための、手法(誤差逆伝搬法など)
- 活性関数・シグモイド関数・ソフトマックス関数などのノードに埋め込む関数
など、数学の知識が必要な領域になっていきます。
しかし、パーセプトロン・ニューラルネットワークの基本的な流れや考え方を理解していれば難しい内容ではありません。
なんなら数学の部分はNumpyなどで簡単に攻略できます。
最後に
今回はDeepLearningの学習で非常に大事なニューラルネットワークの本質を掴んでもらえるような説明にしました。ニューラルネットワークを理解すれば「教師あり・なし学習、強化学習の違い」や「人工知能に関するニュースの見え方」が大きく変わってきます。
この記事を読んでDeepLearningへの壁が少しでも減らせれば幸いです。
明日は我らがYasuhiro Kunimotoさんによる記事です!
お楽しみに👍